Для решения задач интерполяции и аппроксимации данных функций, заданных рядом узловых точек, используются следующие функции.
| InterpolatingPolinomial[data, var] Interpolation[data] Interpolation[data][x] InterpolationOrder | Интерполирует данные списка data степенным многочленом по переменной var. Данные могут иметь форму: {{x1,f1},{x2,f2}, …} или {f1,f2, …},причем xi принимают значения 1,2, … или вместо fi можно задавать {fi,dfi.ddfi, …}, указывая производные в точках xi Конструирует объект InterpolationFunction, который представляет собой приближенную функцию, интерполирующую данные data. Данные могут иметь форму: {{x1,f1},{x2,f2},…} или {f1,f2, …},причем xi принимают значения 1,2, …, вместо fi можно задавать {fi,dfi.ddfi, …}, указывая производные в точках xi Находит значение интерполяционной функции в конкретной точке x. Опция к функции, которая указывает степень подходящего полинома. |
Примеры:
1) Найти интерполяционный многочлен по точкам: (1,2),(2,5),(3,10)
Вводим
Получим тот же результат, введя:
2) Найдем интерполяционную функцию по точкам 
соответственно
3) Для второго примера найдем значение интерполяционной функции в конкретной точке x, но при этом мы не видим саму функцию, поэтому применим графику:
Оператор Fit вычисляет параметры функции, при которых среднеквадратичная погрешность между результатами вычислений по этой функции и совокупностью исходных данных минимальна.
| Fit[data,funs,vars] | Аппроксимирует дискретные данные data в виде линейной комбинации функций funs переменных vars |
В отличие от интерполяции, функция в узловых точках не дает точного значения ординат – она просто минимизирует в них погрешности вычислений.
Следующий оператор позволяет найти минимум функции, который используется при решении задач оптимизации:
| FindMinimum[f,{x,x0}] | Ищет локальный минимум функции f(x) в окрестности точки x0. |
Пример:
Для заданного массива данных получим приближение в виде многочлена второй степени и суммы экспонент.
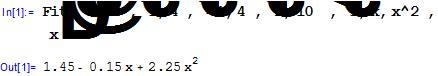
Упражнения:
1) Постройте интерполяционный многочлен по точкам: (-3, -27), (-2, -8), (-1, -1), (0, 0), (1, 1), (2, 8), (3, 27).
2) Аппроксимируйте многочленом 
функцию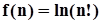 
при помощи метода наименьших квадратов, взяв в качестве исходных данных точки 
, 
(использовать Fit).
3) Постройте с помощью функции ListPlot массив точек 
, а затем аппроксимируйте
4) многочленом 
и интерполяционным многочленом, взяв за исходные точки массива, и сопоставьте полученные данные на графике.
9. Приложение к химической технологии
Расчет пылеосадительной камеры
Рассчитать пылеосадительную камеру полочного типа для грубой очистки газа, загрязненного твердыми частицами, расхода 
м3/ч, при давлении P=750 мм.рт.ст. Средняя температура газа, проходящего через камеру, 
°С. Минимальный размер улавливаемых частиц d м. Плотность газа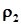 
кг/м3, кинематическая вязкость 
м2/с.
Если расход поступающего газа равен V, тогда действительный секундный расход газа поступающего в пылеосадительную камеру при заданной температуре вычисляется по формуле
1) Если вы хотите на экране увидеть, чему равен действительный секундный расход, то в цикле For вы должны добавить функцию Print[Vсек[i]].
2) Здесь также используется // N - для чего? N - сообщает МАТЕМАТИКЕ, что в данный момент нам нужен численный результат вычисления (так как МАТЕМАТИКА может дать результат в виде дроби), и по умолчанию МАТЕМАТИКА дает его с шестью значащими цифрами.
3) Объемный расход вводился в виде массива, а работать нужно с его элементами; в МАТЕМАТИКЕ выделение элемента из массива происходит с помощью двойных квадратных скобок: V[[i]]
4) Оператор For[start,test,step,expr] - вычисляет начальное значение start, потом, повторяясь, вычисляет step (шаг) и ехрr (выражение), пока test (условие) не примет значение False.
