Арифметические выражения для ввода составляются с использованием знаков арифметических действий и с соблюдением порядка действий (с использованием круглых скобок, если это необходимо).
| x y z или x*y*z x+y+z x–y x/y x^y | Умножение: знак умножения или пробел
сложение
вычитание
деление
возведение в степень (записано  )
|
Обратите внимание, что при умножении числа, записанного цифрами, на переменную ни знак *, ни знак пробела можно не ставить, при этом запись вида 3x будет восприниматься как умножение, в отличие от записи x3, которую Mathematica будет трактовать как переменную.
Примеры:
Вычислим значение выражения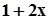 
при 
 |
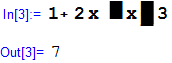Mathematica содержит набор математических функций. Перечислим в таблице некоторые из них.
| Sqrt[x] Exp[x] Log[x] Log[b,x] Sin[x],Cos[x],Tan[x],Cot[x], Sec[x],Csc[x] ArcSin[x],ArcCos[x],ArcTan[x] ArcCot[x], ArcSec[x],ArcCsc[x] n! Abs[x] Random[] Round[x] Max[x,y,…] Min[x,y,…] | Квадратный корень ( )
Показательная функция с основанием e ( )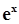
Натуральный логарифм ( )
Логарифм по основанию b ( )
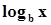Тригонометрические функции радианных аргументов (синус, косинус, тангенс, котангенс, секанс, косеканс соответственно)
Обратные тригонометрические функции
Факториал (произведение всех натуральных чисел от 1 до n)
Абсолютная величина (модуль) числа
Случайное число между 0 и1
Ближайшее к x целое число
Наибольшее из чисел x, y,…
Наименьшее из чисел x, y,…
|
Нужно отметить, что аргументы всех функций в программе Mathematica заключаются в квадратныескобки, а наименования встроенных функций начинаются с заглавных букв.
Примеры:
1) Вычислим 7!;
2) Вычислим точное значение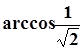 
3) Проверим тригонометрическое тождество
4) Найдем логарифм «случайного» числа по «случайному» основанию и применим функцию Round.
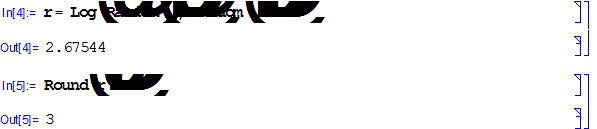
Matematica включает в себя математические константы
| Pi E Degree I Infinity | 
|
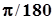
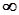
Все эти константы можно ввести с помощью палитры инструментов BasicInput.
Примеры:
1) Вычислим натуральный логарифм от 
2) Вычислим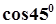 
Указанные основные элементарные функции позволяют строить самые разнообразные функции. В реальных программах эти функции используются не в чистом виде, а в комбинациях. Рассмотрим на примерах:
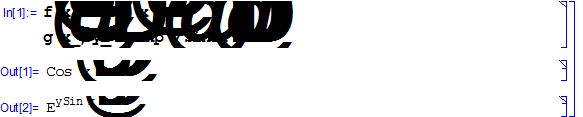
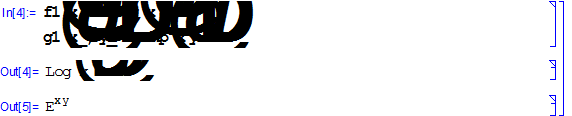
Рассмотрены суперпозиции некоторых функций.
При определении функции черта снизу после аргумента функции используется для подстановки, которая может существенно изменить исходную функциональную зависимость. В качестве аргумента функции может использоваться любая другая функция или любой другой аргумент.
