Теоретичні відомості про коло

Колом називається множина точок площини, рівновіддалених від даної точки, яка називається центром кола. Рівняння кола з центром у початку координат і радіусом 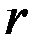має вигляд: .

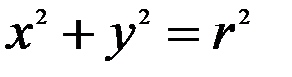Рівняння кола з центром в точці 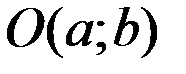і радіусом 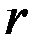має вигляд:

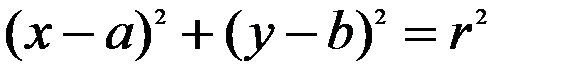
Рівняння кола в загальному вигляді записують так:

,

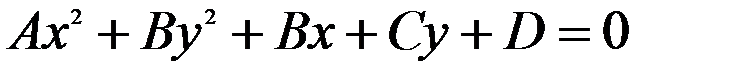де 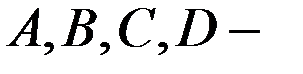сталі коефіцієнти.

Завдання 1. Побудувати коло .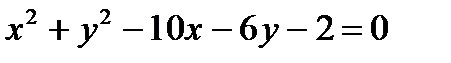

Еліпсом називається множина точок, сума відстаней від яких до двох заданих точок, що називаються фокусами, є величина стала 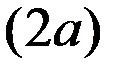, більша за відстань між фокусами 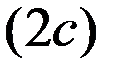. Рівняння еліпса, фокуси якого лежать на осі 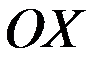, має вигляд:

, ,

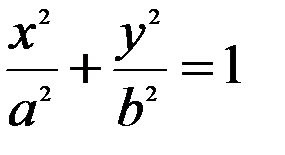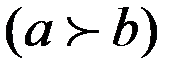де 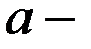довжина великої півосі, 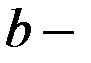довжина малої півосі.

Залежність між параметрами 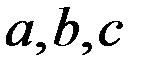виражається співвідношенням: .

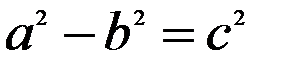Ексцентриситетом еліпса називається відношення фокусної відстані до великої осі:

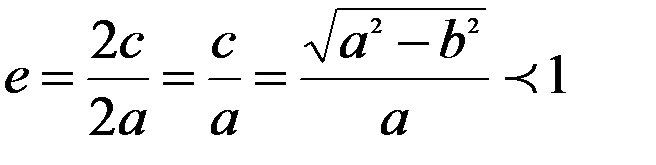
Якщо фокуси еліпса лежать на осі 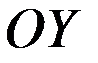, то його рівняння має вигляд:

, .

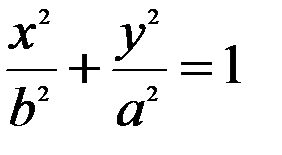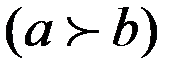В усіх задачах на еліпс передбачено, що осі симетрії еліпса збігаються з осями координат.

 

Задача №2. Скласти рівняння еліпса, якщо його більша вісь дорівнює 10, а ексцентриситет .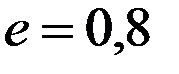

Задача № 3. Дано еліпс 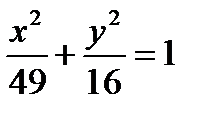. Знайти координати його вершин і довжини осей, ексцентриситет еліпса.

Гіперболою називається геометричне місце точок модуль різниці відстаней для кожної з яких до двох даних фіксованих точок (фокусів) є величина стала, менша за відстань між фокусами і дорівнює 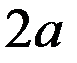. Найпростіше рівняння гіперболи:

,

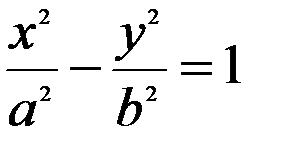де 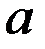- дійсна піввісь гіперболи, 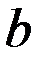- уявна піввісь.

Якщо 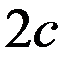- відстань між фокусами, то 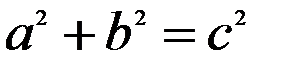. При 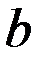= 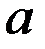гіпербола називається рівносторонньою, її рівняння має вигляд: 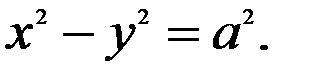Фокуси гіперболи знаходяться на її дійсній осі. Ексцентриситет гіперболи – це відношення фокусної відстані до довжини дійсної осі: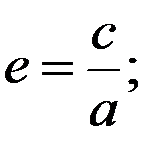

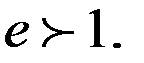
Асимптоти гіперболи – прямі, що задаються рівняннями .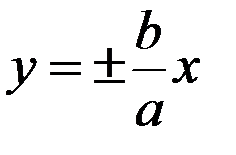

Якщо фокуси гіперболи лежать на осі 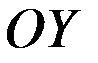, то її рівняння має вигляд:

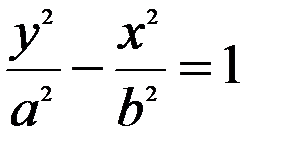або ,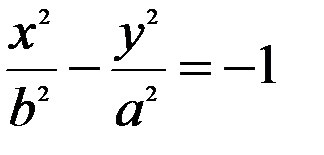

а рівняння асимптот такої гіперболи .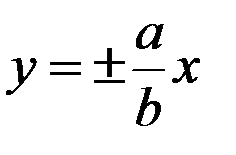

Рівняння рівносторонньої гіперболи з фокусами на осі 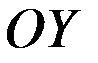має вигляд: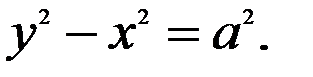

Гіперболи:

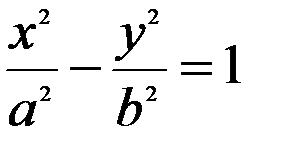і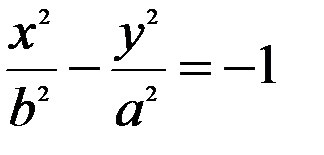

називаються спряженими.

В усіх задачах на гіперболу передбачено, що осі симетрії гіперболи співпадають з осями координат.

Задача №4. Скласти рівняння гіперболи, що має асимптотами прямі 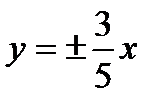і проходить через точку (-5;2).

Задача №5. Скласти рівняння гіперболи, якщо її вершини лежать в точках 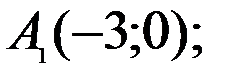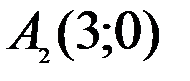і фокуси в точках .

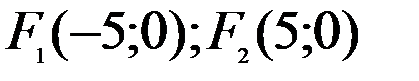Параболою називається геометричне місце точок, кожна з яких однаково віддалена від заданої фіксованої точки (фокуса) і від заданої фіксованої прямої (директриси). Найпростіше рівняння параболи має вигляд: 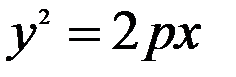, де 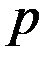- параметр, тобто відстань між директрисою та фокусом. Рівняння директриси 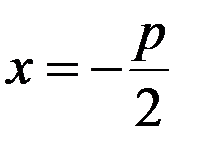, фокус – це точка .

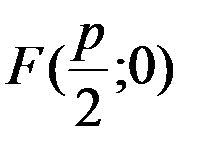Є випадки задання параболи:

1)

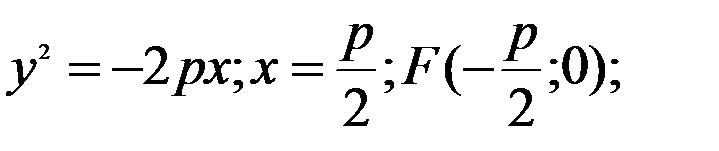
2)

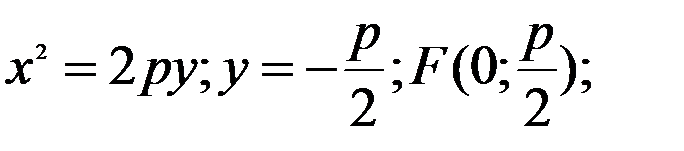
3)

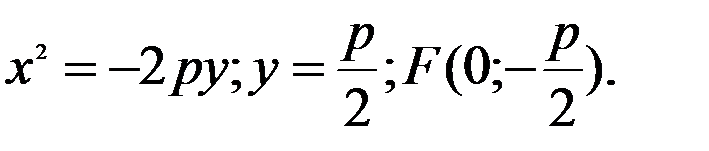
Рівняння парабол зі зміщеною вершиною мають вигляд:

;

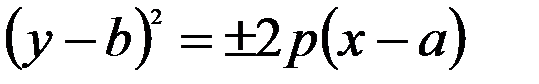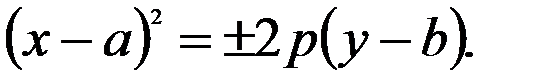
Задача № 6. Визначити координати вершини і величину параметра параболи, рівняння якої: 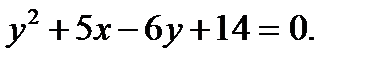Знайти також координати її фокуса і рівняння директриси параболи

Питання для самоперевірки знань, умінь

1. Що називається колом? Що таке центр кола, радіус кола?
2. Що називається еліпсом? Пояснити, чому еліпс є лінією другого порядку?
3. Що таке ексцентриситет еліпса?
4. Як пов’язаний еліпс з колом?

5. Що називається гіперболою? Осі гіперболи, фокуси, вершини.

6. Канонічне рівняння гіперболи. Спряжені гіперболи.

1. Яка гіпербола називається рівносторонньою?
2. Ексцентриситет гіперболи.
3. Рівняння асимптот гіперболи.
4. Що таке парабола? Вершина параболи, фокус, параметр.
5. Що називається директрисою параболи? Рівняння директриси параболи.
6. Як визначити вершину параболи та її параметр, якщо задано рівняння параболи?

 

Висновок__________________________________________________

 

Перевірив викладач ___________ Оцінка__________Дата ___________