Головну, лінійно залежну від Δх, частину приросту Δy функції y=f(x), тобто величину 
, називають диференціалом функції і назначають dy або d(f(x)). Отже, 
.
Диференціал аргументу дорівнює його приросту dх= Δх. Тому 
.
Отже, щоб знайти диференціал функції y=f(x), слід знайти похідну 
цієї функції і помножити цю похідну на диференціал аргументу dx.
Диференціал використовують для наближених обчислень:
- Для дуже малих значень Δх
, тобто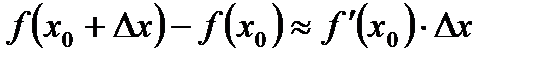 
. - Для знаходження наближених значень функцій використовують формулу:
.
Задача № 1. Обчислити диференціал функції 
при x =π/4 і dx=0,03.
Задача № 2. Знайти наближене значення приросту функції 
в точці 
Задача № 3.
а) Обчислити наближене значення функції 
при x =2,01
б) Знайти наближене значення 
в) Знайти наближене значення 
