Важной задачей статистики является разработка методики статистической оценки социальных явлений, которая осложняется тем, что многие социальные явления не имеют количественной оценки.
Оценка связей социальных явлений осуществляется на основе расчета и анализа специальных коэффициентов: ассоциации, контингенции, взаимной сопряженности, эластичности.
· Для определения тесноты связи двух качественных признаков, каждый из которых состоит только из двух групп, применяются коэффициенты ассоциации (Касс) и контингенции (Кконт).
Для их вычисления строится таблица (табл.2), которая показывает связь между двумя явлениями, каждое из которых должно быть альтернативным, т.е. состоящим из двух качественно отличных друг от друга значений признака (плохой, хороший; светлый, темный….):
Таблица 2
| а | b | a + b |
| c | d | c + d |
| a + c | b + d | a + b + c + d |
Коэффициент ассоциации вычисляется по формуле:
Касс = 
Коэффициент контингенции вычисляется по следующей формуле:
Кконт = 
Коэффициенты ассоциации и контингенции изменяются в пределах от (-1) до (+1), причем коэффициент контингенции всегда меньше коэффициента ассоциации.
Связь между зависимыми явлениями или процессами считается подтвержденной, если Касс > 0,5 или Кконт > 0,3.
· Коэффициенты взаимной сопряженности Пирсона (КП) и Чупрова (КЧ) применяются для определения тесноты связи в том случае, если каждый из качественных признаков состоит более, чем из двух групп.
Коэффициенты определяются по следующим формулам соответственно:
КП = 
КЧ = 
, где:
- показатель взаимной сопряженности,
к1 - число значений (групп) первого признака,
к2 - число значений (групп) второго признака.
Для расчета коэффициента взаимной сопряженности необходимо построить вспомогательную таблицу (табл.3):
Таблица 3
| у x | всего | |||
| ….. ….. ….. | ..… ….. ….. | nxy | nx nx nx | |
| итого | ny | ny | ny | n |
- определяется как сумма отношений квадратов частот каждой клетки таблицы к произведению итоговых частот соответствующего столбца и строки минус 1;
= 
Чем ближе величины КП и КЧ к 1, тем связь теснее или выше.
· С целью расширения возможностей экономического анализа статистической модели экономического процесса или явления используются частные коэффициенты эластичности (Эхi), определяемые по формуле:
, где:
ai - коэффициент регрессии при соответствующем факторном признаке,
- среднее значение соответствующего факторного признака,
- среднее значение результативного признака.
Коэффициент эластичности показывает, на сколько процентов в среднем изменится значение результативного признака при изменении факторного признака на 1%.
Решение типовых задач
9.3.1. Имеются данные о стоимости основных фондов и выпуску продукции по 10 компаниям:
| название компаний | стоимость основных фондов, млн. руб. | выпуск продукции, млн. руб. |
| А | ||
| «Звезда» «Атлант» «Фиас» «Антарис» «Перспектива» «Рамекс» «Алмаз» «Колобок» «Сапфир» «Норд» | 2,4 4,0 3,6 4,0 4,5 4,6 5,6 6,5 7,0 5,0 | |
| итого | 47,2 |
Вычислите коэффициент корреляции по стоимости основных фондов и выпуску продукции компаний.
Решение:
Составим расчетную таблицу для подготовки вычисления коэффициента корреляции, приняв стоимость основных фондов за факторный признак (х), а выпуск продукции за результативный признак (у):
| название компаний | cтоимость основных фондов, млн. руб. (х) | выпуск продукции, млн. руб. (у) | xy | x 2 | y 2 |
| А | |||||
| «Звезда» «Атлант» «Фиас» «Антарис» «Перспектива» «Рамекс» «Алмаз» «Колобок» «Сапфир» «Норд» | 2,4 4,0 3,6 4,0 4,5 4,6 5,6 6,5 7,0 5,0 | 14,4 32,0 32,4 40,0 45,0 50,6 67,2 84,5 98,0 75,0 | 5,8 16,0 13,0 16,0 20,2 21,2 31,4 42,2 49,0 25,0 | ||
| итого | 47,2 | 539,1 | 239,8 |
= 
=
= 
Таким образом, связь между стоимостью основных фондов и выпуском продукции прямая и высокая.
9.3.2. Имеются следующие данные об уровнях издержек обращения и выработке на одного работника, т.е. производительность труда по предприятиям региона за квартал:
| № п/п | средняя выработка на одного работника, тыс. руб.(х) | уровень издержек обращения, % к товарообороту (y) |
| 40,4 | 4,54 | |
| 43,1 | 4,42 | |
| 45,2 | 4,19 | |
| 47,0 | 4,23 | |
| 51,4 | 3,88 | |
| 51,7 | 4,00 | |
| 53,9 | 4,04 | |
| 55,2 | 4,01 |
Постройте уравнение взаимосвязи признаков, влияющих на издержки обращения, и сделайте прогноз работы новых предприятий с выработкой на одного работника 60 тыс. руб.; 50 тыс. руб. и 40 тыс. руб.
Решение:
1. Для подтверждения положений логического (качественного) анализа о наличии прямой зависимости между уровнем издержек обращения и средней выработкой нанесем исходные данные (эмпирические) на график корреляционного поля и сделаем выводы о форме связи:
Из графика видно, что связь является линейной и обратной. Точки расположены по направлению из верхнего левого угла в правый нижний:
с увеличением выработки снижается уровень издержек обращения.
2. Для определения тесноты связи между изучаемыми признаками вычислим линейный коэффициент корреляции.
Для вычисления линейного коэффициента корреляции произведем необходимые расчеты в таблице, так как для расчета r и построения уравнения регрессии (связи) требуются одни и те же показатели.
Расчетная таблица для определения параметров уравнения регрессии:
| № п/п | cредняя выработка одного работника, тыс. руб. x | уровень издержек обращения % к товарообо-роту, y | xy | x² | y² |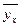 
|
| 40,4 | 4,54 | 183,4 | 1632,16 | 20,61 | 4,47 | |
| 43,1 | 4,42 | 190,5 | 1857,61 | 19,54 | 4,37 | |
| 45,2 | 4,19 | 189,4 | 2043,0 | 17,56 | 4,29 | |
| 47,0 | 4,23 | 198,2 | 2209,0 | 17,89 | 4,22 | |
| 51,4 51,7 | 3,88 4,00 | 199,4 206,8 | 2641,96 2672,89 | 15,05 16,0 | 4,05 4,04 | |
| 53,9 | 4,04 | 217,8 | 2905,21 | 16,32 | 3,96 | |
| 55,2 | 4,01 | 221,4 | 3047,04 | 16,08 | 3,91 | |
| Итого | 387,9 | 33,31 | 1607,5 | 1900.8,87 | 139,05 | 33,31 |
Линейный коэффициент корреляции для парной зависимости исчисляется по следующей формуле:
Абсолютная величина линейного коэффициента корреляции r = - 0,90, что свидетельствует о высокой тесноте связи между изучаемыми признаками, а знак "минус" при коэффициенте - об обратной связи.
3. В целях синтезирования модели в зависимости от уровня издержек обращения и средней выработки определим уравнение прямолинейной связи и нанесем полученную при этом теоретическую линию регрессии на ранее построенный график корреляционного поля.
4. Уравнение прямой линии имеет вид:
где:
- индивидуальные значения результативного признака;
x - индивидуальные значения факторного признака;
- параметры уравнения регрессии.
Способом наименьших квадратов решим систему нормальных уравнений, находя параметры 
и 
:
n aо + a1∑x=∑y,
aо∑x + a1 ∑x²=∑xy 
подставляем значения из расчетной таблицы:
8 aо +387,9 a1 =33,31
387,9 aо + 19008,87 a1 =1607,5
делим каждое уравнение на коэффициенты при а0 (первое уравнение делим на 8, а второе - на 387,9)и получаем:
ао + 48,49 a1 = 4,16
ао + 49,0 a1 = 4,14
вычитаем из второго уравнения первое и получаем:
0,51 a1 = - 0,02.
а1 = -0,039.
подставляем значение a1 в первое уравнение и находим коэффициент а0:
ао + 48,49(-0,039) = 4,16;
ао - 1,89=4,16;
ао = 6,05.
Уравнение корреляционной связи принимает вид:
Свободный член aо характеризует уровень издержек обращения, не зависящий от выработки на одного работника. Коэффициент регрессии a1 уточняет связь между у и х. Он показывает, на сколько единиц увеличивается результативный признак при измерении факторного признака на единицу в пределах установленной вариации. При увеличении выработки на 1 млн. руб. уровень издержек обращения снижается на 0,039% к обороту.
5. Так как уравнение регрессии составлено на основе фактической информации по данным о восьми предприятиях за квартал, то можно исчислить по нему теоретические уровни, т.е. в уравнение 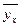= 6,05 - 0,039 х вместо значений х будем подставлять фактические данные о выработке каждого из предприятий:
№1 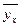= 6,05 - 0,039*40,4 = 4,47;
№2 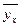= 6,05 - 0,039*43,1 = 4,37 и т.д. (графа 7 расчетной таблицы).
В итоге получим сумму 33,31, которая соответствует графе 3 и свидетельствует о правильности выполненных расчетов.
Полученные значения наносим на ранее построенный график корреляционного поля - это будет теоретическая (сглаженная) прямая линия.
6. Используя полученную информационную математическую модель, определим возможное значение уровня издержек обращения для открываемых в регионе новых предприятий:
· с выработкой на одного работника 60 тыс. руб.:
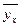= 6,05 - 0,039*60 = 3,71%,
т.е. уровень издержек при этом составит 3,71% к товарообороту за квартал при прочих равных условиях.
· с выработкой на одного работника 50 тыс. руб.:
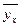= 6,05 - 0,039*50 = 4,1%,
· с выработкой на одного работника 40 тыс. руб.:
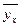= 6,05 - 0,039*40 = 4,49%.
9.3.3. Определите при помощи корреляционного отношения тесноту связи между числом обслуживаемых станков и средней выработкой одного рабочего:
| рабочие | дневная выработка рабочего | отклонение индиви-дуальных значений признака от общей средней
| сумма квадратов отклонений индивидуальных значений признака от общей средней
| |||
| на 8 станках | на 11 станках | на 8 станках | на 11 станках | на 8 станках | на 11 станках | |
| А | ||||||
| -14 -6 -11 -9 -10 | +8 +12 +6 +14 +10 | |||||
| итого |
Решение:
Определим среднюю выработку рабочего на 8 станках:
дет.
Определим среднюю выработку рабочего на 11 станках:
дет.
Общая средняя выработка всех рабочих равна:
дет.
Вычислим общую дисперсию (
), характеризующую общую вариацию под влиянием всех факторов:
Межгрупповая дисперсия (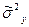
), х арактеризующая факторную вариацию, т.е. различия в выработке, обусловленные неодинаковым числом обслуживаемых станков, определяется по формуле:
= 
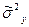дет.
Рассчитаем корреляционное отношение по следующей формуле:
h = 
или 96,4%
Следовательно, 96,4% всей вариации выработки объясняется тем, что часть рабочих работали на 8 станках, а часть рабочих работали на 11 станках и только 3,6% вариации (100% - 96,4%) является результатом действия прочих случайных факторов, не положенных в основание группировки.
9.3.4. По данным о сумме активов, кредитных вложений и величине собственного капитала коммерческих банков одного из регионов Российской Федерации на 01.01.2010 года постройте множественное уравнение связи. Связь предполагается линейной:
| номер банка | сумма активов, млн.руб. (у) | кредитные вложения, млн.руб. (х1) | собственный капитал, млн.руб. (х2) |
| итого |
По полученным данным рассчитайте коэффициент эластичности взаимосвязи признаков.
Решение:
Уравнение множественной регрессии:
Система нормальных уравнений имеет вид:
Построим расчетную таблицу для определения параметров уравнения регрессии:
| но-мер бан-ка | сумма акти-вов, млн. руб. (у) | кре-дит-ные вло-же-ния, млн. руб. (х1) | собс-твен-ный капи-тал, млн. руб. (х2) | ух1 | 
| у2 | х1х2 | 
| ух2 |
|
| ∑ |
Подставим полученные значения в систему уравнений:
7 а0 + 867 а1 +104 а2 = 14757
8671 а0 + 14266159 а1 + 1510415 а2 = 21956214
1046 а0 + 1510415 а1 + 175876 а2 = 2534726.
Отсюда: а0 = - 443,4; а1 = 0,0368; а2 = 16,77
Уравнение множественной регрессии имеет вид:
- 443,4 + 0,0368 х1 + 16,77 х2.
Произведенные расчеты показали, что с увеличением кредитных вложений на 1 млн. рублей и собственного капитала коммерческих банков на
1 млн. рублей стоимость их активов возрастает соответственно в среднем на 0,0358 млн. рублей и 16,77 млн. рублей.
Коэффициент эластичности (Эхi) определяется по формуле:
Подставляя значения признаков определим влияние каждого факторного признака на результативный признак отдельно:
.
Это означает, что при увеличении кредитных вложений и собственного капитала на 1% стоимость активов в среднем возрастает соответственно на 0,02% и 1,19%.
9.3.5. Исследовалась социально-демографическая характеристика потребления сигарет женщинами в зависимости от их семейного положения в одном из регионов Российской Федерации.
Результаты обследования характеризуются следующими данными
(тыс. чел.):
| группы курящих женщин | семейное положение | всего | |
| замужем | не замужем | ||
| курит сигареты не курит сигареты | 10,0 2,5 | 14,5 4,5 | 24,5 7,0 |
| итого | 12,5 | 19,0 | 31,5 |
Рассчитайте коэффициенты ассоциации и контингенции.
Решение:
Касс = = 
= 0,108
Кконт 
Так как Касс < 0,5 и Кконт < 0,3, то потребление сигарет женщинами не зависит от их семейного положения.
9.3.6. Исследовалась зависимость между оценкой уровня жизни респондентов г.Ярославля и формой собственности предприятия, на котором они работают:
| форма собственности предприятия | оценка уровня жизни респондентов | итого | |||
| вполне удовлетво-рительно | скорее удовлетво-рительно | скорее не удовлетво-рительно | совсем не удовлетво-рительно | ||
| государственная | |||||
| муниципальная | |||||
| смешанная российская | |||||
| частная | |||||
| итого |
Определите коэффициенты взаимной сопряженности Пирсона и Чупрова.
Решение:
Для определения коэффициентов необходимо сделать вспомогательные расчеты: 
=0,636 + 0,249 + 0,047 + 0,100 = 1,032
= 1,032 – 1 = 0,032
Коэффициент взаимной сопряженности Пирсона определяется по формуле:
КП = = 
Коэффициент взаимной сопряженности Чупрова определяется по формуле:
КЧ = 
Так как коэффициенты взаимной сопряженности КП и КЧ по своим значениям далеки от единицы, то можно сказать, что оценка уровня жизни респондентов не зависит от типа предприятия, на котором они работают.
9.3.7. Имеются данные зависимости наличияотдельной квартиры от семейного положения человека:
| семейное положение | наличие отдельной квартиры | отсутствие отдельной квартиры | всего |
| семейные | 300 (а) | 115 (b) | 415 (a + b) |
| одинокие | 15 (с) | 70 (d) | 85 (c + d) |
| всего | 315 (а + с) | 185 (b + d) |
Вычислите коэффициенты ассоциации и контингенции зависимости данных явлений.
Решение:
Коэффициент ассоциации рассчитывается по следующей формуле:
Касс = = 
Коэффициент контингенции определяется по формуле:
Кконт = = 
Так как полученный Касс > 05, а коэффициент контингенции Кконт > 0,3, значит между семейным положением и обеспеченностью отдельной квартирой существует прямая умеренная связь.
