Задача 1.
По данным группировки 40 предприятий потребительской кооперации по величине балансовой прибыли и объему продукции постройте уравнение связи:
| балансовая прибыль, тыс. руб. (у) | объем продукции, тыс. руб. (х) | |||||
| 100-200 | 200-300 | 300-400 | 400-500 | 500-600 | итого (fy) | |
| 10-20 | ||||||
| 20-30 | ||||||
| 30-40 | ||||||
| 40-50 | ||||||
| 50-60 | ||||||
| итого (fx) |
Задача 2.
Имеются следующие данные о производительности труда портних швейной фабрики, выполняющих одинаковые операции:
| группы портних по стажу работы | число портних | дневная производительность труда, шт. | дисперсия производительности труда в группе |
| до 5 лет | 5,3 | ||
| 5-10 лет | 1,8 | ||
| более 10 лет | 1,1 |
Определите степень тесноты связи между уровнем производительности труда портних и стажем их работы.
Задача 3.
По данным о сумме активов и кредитных вложений коммерческих банков одного из регионов Российской Федерации на 01.01.2011 года определите направление и тесноту взаимосвязи между признаками, выделив кредитные вложения факторным признаком, а сумму активов – результативным признаком):
| номер банка | кредитные вложения, млн. руб. | сумма активов, млн. руб. |
| итого |
Задача 4.
Изобразите графически в корреляционном поле следующие данные о зависимости объема продаж облигаций на ММВБ 01.01.2011 г. и доходности к погашению:
| группы серий по объему продаж, млрд. руб. (х) | группы серий по доходности к погашению, % (у) | всего серий | |||
| 42 - 49 | 49 - 56 | 56 - 63 | 63 - 70 | ||
| 3 - 61 61 – 117 117 – 187 187 – 231 231 – 292 292 - 339 | |||||
| итого |
Рассчитайте средние величины групп (
) и постройте эмпирическую линию регрессии.
Задача 5.
Для оценки степени тесноты связи между уровнем выработки рабочих и стажем их непрерывной работы была рассчитана величина корреляционного отношения, оказавшая равной 0,85 при объеме выборки равном 100 (п = 100).
Определите величину средней внутригрупповой дисперсии, если известно, что общая дисперсия выработки рабочих составляет 5,9.
Задача 6.
Взаимосвязь между стоимостью активной части основных фондов и затратами на производство работ по 35 строительным фирмам представлена следующей таблицей:
| затраты на производство строительно-монтажных работ, % к стоимости активной части основных фондов | стоимость активной части основных фондов, млн. руб. | всего фирм | |||
| 50-100 | 100-150 | 150-200 | 200-250 | ||
| 1 - 6 6 - 11 11 - 16 16 - 21 21 - 26 | |||||
| итого |
Постройте в корреляционном поле эмпирическую линию регрессии.
Задача 7.
Имеются данные о связи между четырьмя показателями, характеризующими экспорт технологий и услуг технического характера по 10 областям Российской Федерации в 2010 году (млн. евро):
| номер области | число соглашений | стоимость предмета соглашения | чистая стоимость предмета соглашения | поступления по соглашениям |
| 0,51 3,29 0,11 3,69 0,51 5,10 0,52 1,75 4,38 3,37 | 0,51 3,28 0,11 3,69 0,51 5,06 0.51 1,74 4.31 3,35 | 0,42 0,18 0,11 2,38 O,51 2,04 0,52 0,28 3,31 0.29 |
Определите вид корреляционной зависимости между показателями числа соглашений и стоимости предмета соглашения по экспорту технологий и услуг, найдите параметры уравнения регрессии. Определите направление и тесноту связи.
Задача 8.
Имеются следующие данные о работниках потребительской кооперации в одном из регионов Российской Федерации:
| группы работников по стажу работы | число работников в группе | средняя месячная заработная плата, руб. | дисперсия месячной заработной платы в группе |
| до 5 лет 5 лет и более |
Определите степень тесноты связи между стажем работы и размером заработной платы работников.
Задача 9.
Имеются данные о связи между средней взвешенной ценой и объемом продаж облигаций на ММВБ 01.01.2011 г.:
| номер серии | средняя взвешенная цена, тыс. руб. (х) | объем продаж, млрд. руб. (у) |
| A B C D E F G H I J | 73,29 81,38 80,21 59,43 88,24 79,32 76,58 77,05 72,86 74,12 | 80,3 259,9 84,2 301,4 68,7 63,5 234,1 71,6 67,3 312,5 |
Составьте линейное уравнение регрессии. Вычислите параметры и рассчитайте линейный коэффициент корреляции.
Сформулируйте выводы.
Задача 10.
По 20 предприятиям легкой промышленности получена математическая модель, отражающая зависимость выпуска продукции (у) за месяц от размера основного капитала (х):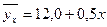 
.
Кроме этого, по всей совокупности предприятий имеются следующие данные:
1) средняя стоимость основного капитала на одно предприятие -
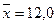млн. руб;
2) средний размер выпуска продукции на одно предприятие –
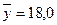млн. руб.;
3) среднее квадратическое отклонение по стоимости основного капитала -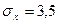 
млн. руб.;
4) среднее квадратическое отклонение по размеру выпуска продукции -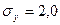 
млн. руб.
Определите степень тесноты связи между размером выпуска продукции и стоимостью основного капитала указанных предприятий легкой промышленности.
Задача 11.
Зависимость между объемом произведенной продукции и балансовой прибылью по 10 предприятиям характеризуется следующими данными:
| номер предприятия | объем реализованной продукции, млрд. руб. | балансовая прибыль, млрд. руб. |
| 567,6 479,2 485,4 499,6 431,9 488,7 533,4 457,6 412,8 495,3 | 157.6 120,8 64,3 59,0 48,7 69,4 98,9 43,6 105,1 111,9 |
Определите вид корреляционной зависимости. Постройте уравнение регрессии, рассчитайте параметры уравнения, вычислите тесноту связи.
Сформулируйте выводы.
Задача 12.
Имеются следующие данные о зависимости между объемом продаж облигаций на ММВБ и доходностью к их погашению:
| группы серий по объему продаж, млрд. руб. (х) | группы серий по доходности к погашению, % (у) | всего серий | |||
| 43 - 50 | 50 - 57 | 57 - 64 | 64 - 71 | ||
| 2 - 59 59 - 112 112 - 177 177 - 214 214 - 286 286 - 340 | |||||
| итого |
Определите вид корреляционной зависимости между объемом продаж облигаций на ММВБ и доходностью к их погашению.
Найдите параметры уравнения регрессии, определите тесноту связи.
Сформулируйте выводы.
Задача 13.
Имеются следующие данные о стоимости основных фондов и среднесуточной переработке сырья на предприятиях региона:
| стоимость основных фондов, тыс. руб. | среднесуточная переработка сырья, кг | итого | |||
| 200 - 400 | 400 -600 | 600 - 800 | 800 - 1000 | ||
| 300-400 400-500 500-600 600-700 700-800 | |||||
| итого |
Определите вид корреляционной зависимости, найдите параметры уравнения регрессии определите тесноту связи.
Сформулируйте выводы.
Задача 14.
По следующим данным постройте линейное уравнение регрессии:
а0 = 3,5; rxy = 0,85;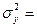 
36; 
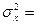49.
Задача 15.
В результате опроса, проведенного в 2010 году Всероссийским центром изучения общественного мнения по отношению к решениям, принимаемым правительством Российской Федерации, мужчин и женщин, получены следующие результаты:
| пол | положи-тельное | отрица-тельное | безраз-личное | итого | частоты | итого | ||
| положи-тельное | отрица-тельное | безраз-личное | ||||||
| женщины | 0,125 | 0,8025 | 0,0725 | |||||
| мужчины | 0,125 | 0,75 | 0,125 | |||||
| итого | 0,125 | 0,775 | 0,100 |
Определите коэффициент взаимной сопряженности и сделайте вывод об отношении населения к решениям, принимаемым правительством страны, в зависимости от пола опрошенных людей.
Задача 16.
В результате обследования работников предприятия получены следующие данные:
| образование | удовлетворены своей работой | не удовлетворены своей работой | итого |
| высшее и среднее | |||
| незаконченное среднее | |||
| итого |
Оцените тесноту связи между уровнем образования и удовлетворенностью своей работой с помощью коэффициентов ассоциации и контингенции.
____
??? ВОПРОСЫ ДЛЯ САМОКОНТРОЛЯ
1. Основные задачи изучения и измерения связи между явлениями?
2. Характеристика функциональной связи явлений и процессов?
3. Понятие корреляционной связи и ее сущность?
4. Виды связей по своему направлению?
5. Характеристика прямолинейной и криволинейной связей, а также их
математическое выражение?
6. Статистические методы установления связей между явлениями?
7. Для каких целей при установлении связи между явлениями применяют
аналитические группировки?
8. Корреляционное отношение, его исчисление и характеристика?
9. Сущность и назначение корреляционного анализа?
10.Определение теоретического значения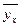 
способом наименьших квадратов?
11.Уравнение регрессии и характеристика его коэффициентов?
12.Определение линейного коэффициента корреляции?
13.Коэффициент эластичности, его сущность и определение?
14.Когда применяются коэффициенты ассоциации и контингенции и порядок
их вычисления?
15.В каких случаях применяются коэффициенты взаимной сопряженности
Пирсона и Чупрова и порядок их исчисления?
