В общем случае работа A, совершаемая силой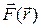 
по перемещению частицы из точки B 1(x 1, y 1, z 1) в точку B 2(x 2, y 2, z 2), определяется с помощью криволинейного интеграла:
(45)
где 
– скалярное произведение векторов силы 
и элементарного перемещения 
.
Расчет мгновенной P и средней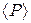 
мощности выполняется по формулам:
(46) 
(47)
где δA – элементарная работа, производимая силой за время dt,
A – полная работа силы за время t.
Если при прямолинейном перемещении частицы работа совершается силой 
не зависящей от координат, то формула (45) упрощается и принимает вид:
(48)
где a – угол между векторами силы и перемещения 
При вращении абсолютно твердого тела вокруг неподвижной оси Oz внешняя сила, создающая момент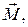 
совершает работу:
(49)
где Mφ – проекция вектора 
на направление вектора угловой скорости, Mφ = ± Mz. Знак работы зависит от знака Mj.
Если момент сил относительно оси Mz постоянен, а начало отсчета угла поворота совпадает с началом действия силы (
= 0), то
(50)
Потенциальная энергия частицы массой m, которая находится вблизи поверхности Земли на высоте h, измеренной от произвольно выбранного нулевого уровня, рассчитывается согласно уравнению
. (51)
При условии, что потенциальная энергия недеформированного (x = 0) тела принимается равной нулю, потенциальная энергия стержня или пружины при их малом растяжении или сжатии вычисляется по выражению:
(52)
где x – смещение точек деформированных тел от положения равновесия;
k – коэффициент упругости (жесткость) пружины или стержня.
Потенциальная энергия гравитационного взаимодействия двух частиц массами m 1 и m 2, расстояние между которыми r, определяется по формуле:
(53)
Напомним, что взаимосвязь консервативной силы с потенциальной энергией устанавливается выражением
(54)
Многие задачи легко решить, воспользовавшись теоремой об изменении кинетической энергии: приращение кинетической энергии системы частиц (твердого тела) равно сумме работ всех внешних и внутренних сил и моментов этих сил, действующих на частицы системы (твердое тело):
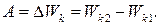(55)
Коэффициент полезного действия (КПД) механизма определяется отношением полезной (A пол) и совершенной механизмом (A сов) работ:
(56)
Кинетическая энергия частицы массой m, движущейся со скоростью 
а также кинетическая энергия абсолютно твердого тела массой m, движущегося поступательно со скоростью определяется по формуле:
(57)
Кинетическая энергия абсолютно твердого тела (АТТ), вращающегося вокруг неподвижной оси Oz с угловой скоростью 
, определяется по формуле:
(58)
где Iz – момент инерции тела относительно оси Oz.
Кинетическая энергия АТТ при его плоском движении может быть вычислена как сумма кинетической энергии поступательного и вращательного движений тела по формуле:
(59)
где v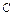 
– скорость движения центра масс тела;
I 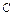– момент инерции тела относительно оси вращения, проходящей через центр масс.
Полная механическая энергия тела, движущегося во внешнем потенциальном поле сил, равна сумме его кинетической и потенциальной энергий:
(60)
В отсутствие диссипативных сил к механической системе применим закон сохранения механической энергии: механическая энергия замкнутой консервативной системы тел остается постоянной, при взаимодействиях тел она может переходить из кинетической энергии в потенциальную и обратно.
В общем случае, в том числе при наличии диссипативных сил (например, сил трения), когда механическая энергия может переходить в другие виды энергии, в частности во внутреннюю, выполняется общефизический закон сохранения энергии: во всех процессах, происходящих в природе, энергия ниоткуда не возникает, никуда не исчезает, а лишь переходит из одной формы в другую.
Задачи
51.(1) Автомобиль массой 1,25 т движется вверх по наклонному участку дороги с постоянной скоростью 36 км/ч. Длина участка дороги равна 150 м, угол ее наклона к горизонтали составляет 15°. Коэффициент сопротивления равен 0,051. Найти работу равнодействующей всех сил, действующих на автомобиль, и работу каждой силы в отдельности, считая эти силы постоянными.
52.(2) Две частицы массой 2,7 кг каждая, находящиеся первоначально на расстоянии 14 см друг от друга, начинают движение навстречу друг другу вследствие гравитационного взаимодействия. Какова работа гравитационной силы за время, прошедшее от начала движения до момента, когда расстояние между частицами стало равным 2,0 см?
53.(2) Тело массой 5,0 кг бросили с земли вертикально вверх со скоростью 5,0 м/с. С какой скоростью тело упало на землю, если сила сопротивления воздуха на всем пути совершила работу, равную -25 Дж?
54.(3) Сила тяги локомотива линейно возрастает от 33 МН до 66 МН на пути длиной 1,2 км. Какова работа силы тяги за это время?
55.(3) К однородному покоящемуся шару массой 2,1 кг и радиусом 4,2 см в точке, наиболее удаленной от оси вращения, совпадающей с осью симметрии, приложили касательную силу 22 Н, перпендикулярную оси вращения. Найти работу этой силы за 11 с от начала вращения шара. Трением на оси пренебречь.
56.(2) Найти кинетическую энергию велосипеда (с велосипедистом), движущегося со скоростью 9,3 км/ч. Масса велосипеда вместе с велосипедистом равна 80 кг, причем на колеса приходится масса 3,0 кг. Колеса считать обручами. Скольжения нет.
57.(2) Определить работу силы тяжести при падении тела массой 3,7 кг с высоты, равной половине радиуса Земли, на ее поверхность.
58.(2) Камень бросили с Земли со скоростью 12 м/с вверх под углом к горизонту. Найти модуль скорости камня на высоте 4,5 м над Землей.
59.(2) Пружина жесткостью 530 Н/м была первоначально сжата силой 140 Н. Затем к пружине приложили дополнительную сжимающую силу. Определить работу дополнительной силы, если пружина под ее действием оказалась сжатой еще на 2,5 см.
60.(3) Шар и обруч одинаковой массы скатываются без скольжения с наклонной плоскости высотой 0,25 м. Во сколько раз будут отличаться значения скоростей центров шара и обруча у основания наклонной плоскости?
