| Лекция 2. | Понятия о дифференциальных уравнениях, их классификация. Физические задачи, приводящие к дифференциальным уравнениям. Дифференциальные уравнения первого порядка. Задача Коши. Формулировка теоремы существования и единственности решения задачи Коши. Частное и общее решение. Основные классы уравнений, интегрируемых в квадратурах (уравнения с разделенными и разделяющимися переменными). |
| Уравнения, интегрируемые в квадратурах (однородное, линейное, Бернулли, в полных дифференциалах). | |
| Лекция 3. | Дифференциальные уравнения высших порядков. Задача Коши. Основные понятия. Интегрирование некоторых уравнений, допускающих понижение порядка. Линейные уравнения второго порядка, однородные и неоднородные. Теоремы о структуре общего решения. |
| Решение линейных уравнений второго порядка с постоянными коэффициентами. Уравнения с правой частью специального вида. | |
| Метод вариации произвольных постоянных как метод нахождения общего решения неоднородного уравнения. Приложения к описанию линейных моделей*. | |
| Нормальная система дифференциальных уравнений. Матричная запись системы. Геометрический смысл решения. Фазовая плоскость (пространство), фазовая кривая. Задача Коши. Решение систем линейных уравнений с постоянными коэффициентами*. | |
| Раздел 11. Числовые и функциональные ряды. Ряды Фурье. | |
| Лекция 4. | Числовые ряды. Сумма и сходимость ряда. Свойства сходящихся рядов. Необходимый признак сходимости ряда с положительными членами. Достаточные признаки сходимости. Признаки сравнения. |
| Признаки Даламбера, Коши, интегральный признак Коши. | |
| Знакопеременные и знакочередующиеся ряды. Теорема Лейбница. Абсолютная и условная сходимость*. | |
| Функциональные ряды, область сходимости. Степенные ряды. Теорема Абеля. Радиус и интервал сходимости. Интегрирование и дифференцирование степенных рядов*. | |
| Ряды Тейлора и Маклорена. Достаточное условие разложимости функции в ряд Тейлора. Разложение в ряд Маклорена некоторых элементарных функций. Применение рядов (приближенное вычисление значений функции, интегрирование функции и дифференциальных уравнений*). | |
Ряды Фурье. Разложение периодической функции с периодом 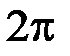 и и  в ряд Фурье. Ряд Фурье для четных и нечетных функций. Периодическое продолжение функций четным и нечетным образом. Применение тригонометрических рядов Фурье в приближенных вычислениях*. в ряд Фурье. Ряд Фурье для четных и нечетных функций. Периодическое продолжение функций четным и нечетным образом. Применение тригонометрических рядов Фурье в приближенных вычислениях*.
| |
| IV семестр | |
| Раздел 12. Теория вероятностей | |
| Лекция 1. | Предмет теории вероятностей. Случайные события и их виды. Различные подходы к определению вероятности: классический, статистический, аксиоматический. |
| Элементы комбинаторики. Алгебра событий. Правило сложения вероятностей. Правило умножения вероятностей. | |
| Формула полной вероятности. Формула Байеса. Повторные испытания. Схема Бернулли. Формула Бернулли. | |
| Понятие случайной величины. Виды случайных величин. Дискретные случайные величины. Ряд распределения. Функция распределения, ее свойства. Некоторые законы распределения. Математическое ожидание и дисперсия дискретной случайной величины. | |
| Лекция 2. | Непрерывные случайные величины. Функция распределения, плотность распределения, их взаимосвязь и свойства. Математическое ожидание и дисперсия. Типовые распределения. Нормальный закон распределения. Понятие о различных формах закона больших чисел*. Центральная предельная теорема Ляпунова*. |
| Раздел 13. Основные понятия и методы математической статистики. Статистические методы обработки экспериментальных данных. | |
| Лекция 3. | Основные понятия математической статистики. Генеральная совокупность и выборка. Вариационный ряд. Гистограмма, эмпирическая функция распределения, выборочные средняя и дисперсия. |
| Статистические оценки числовых характеристик. Точечные оценки: Общие свойства: несмещенность, состоятельность, эффективность, достаточность. Методы получения точечных оценок неизвестных параметров распределения: метод максимального правдоподобия. | |
| Лекция 4. | Интервальные оценки. Доверительный интервал и доверительная вероятность. Построение доверительного интервала для математического ожидания и дисперсии нормально распределенной случайной величины. Статистическая проверка статистических гипотез. Общая постановка задачи. Виды гипотез. Критическая область, уровень значимости и мощность критерия. |
| Ошибки первого и второго рода. Непараметрические гипотезы. Проверка гипотезы о законе распределения по критерию Пирсона. Параметрические гипотезы. Проверка гипотез о параметрах нормально распределенной генеральной совокупности. Понятие о критериях согласия. Проверка непараметрической гипотезы по критерию Пирсона. Статистическая и корреляционная зависимости. Уравнение регрессии. Две основные задачи теории корреляции. |
Примечание. Вопросы, помеченные в содержании лекций значком *, выносятся на самостоятельное
изучение.






