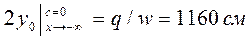При исследовании плоского фильтрационного потока, подчиняющегося закону Дарси, можно использовать теорию функций комплексного переменного. Совместим плоскость комплексного переменного z = x+iy с основной плоскостью течения.
Для каждого плоского фильтрационного потока можно найти характеристическую функцию течения, или комплексный потенциал F(z), который является функцией комплексного переменного z. В функции F(z) можно отделить действительную часть от мнимой
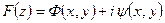 (IV.21)
(IV.21)
где Ф(x, у) — потенциал скорости; ψ(x, у) —функция тока. Эти функции связаны между собой уравнениями Коши — Римана.
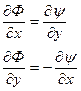 (IV.22)
(IV.22)
и подчиняется уравнению Лапласа
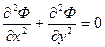 ,
, 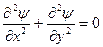 (IV.23) Уравнение
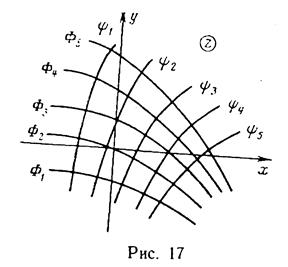
(IV.23) Уравнение 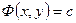 определяет собой семейство эквипотенциалей, совпадающих с изобарами, так как
определяет собой семейство эквипотенциалей, совпадающих с изобарами, так как 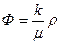 , а
, а 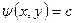 - семейство линий тока. Эквипотенциали и линии тока взаимно ортогональны (рис.17).
- семейство линий тока. Эквипотенциали и линии тока взаимно ортогональны (рис.17).
Проекции скорости фильтрации на координатные оси находят по формулам
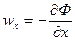 ,
,  (IV.24)
(IV.24)
а модуль скорости фильтрации
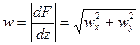 (IV.25)
(IV.25)
Время движения частицы жидкости вдоль линии тока s можно определить по формуле
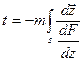 (IV.26)
(IV.26)
где 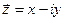 — сопряженное с z комплексное переменное.
— сопряженное с z комплексное переменное.
Если какой-либо сложный плоский фильтрационный поток можно представить как результат наложения нескольких простейших потоков, то характеристическая функция сложного потока равна по принципу суперпозиции алгебраической сумме характеристических функций простейших потоков.
Задача 38
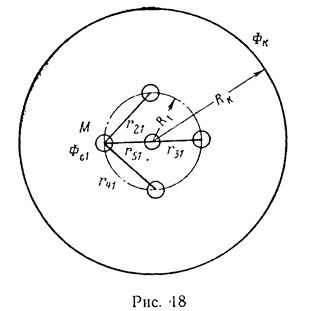 Определить дебит батареи из четырех скважин, расположенных вдали от контура питания, и одной скважины, находящейся в центре (рис. 18), если известно, что все скважины находятся в одинаковых условиях; радиус батареи R1 = 200 м, расстояние до контура питания Rk = 10 км, радиус скважины гс = 0,1 м, мощность пласта h = 10 м, потенциал на контуре питания Фk = 40 см2/с, потенциал на скважинах Фс = 30 см2/с.
Определить дебит батареи из четырех скважин, расположенных вдали от контура питания, и одной скважины, находящейся в центре (рис. 18), если известно, что все скважины находятся в одинаковых условиях; радиус батареи R1 = 200 м, расстояние до контура питания Rk = 10 км, радиус скважины гс = 0,1 м, мощность пласта h = 10 м, потенциал на контуре питания Фk = 40 см2/с, потенциал на скважинах Фс = 30 см2/с.
Решение. Будем исходить из формулы для потенциала при работе группы скважин
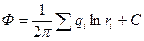 (IV.27)
(IV.27)
Учитывая, что скважины расположены вдали от контура питания, в точке, помещенной па контуре питания, получим
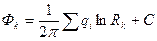 (IV.28)
(IV.28)
Помещая точку М на забой первой скважины и учитывая, что 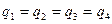 ,будем иметь
,будем иметь
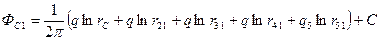 (IV.29)
(IV.29)
Вычитая из (IV.28) (IV.29) и заменяя (см. рис. 18)
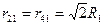 ,
, 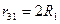 ,
, 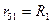
получим
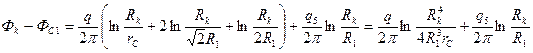 (IV.30)
(IV.30)
Помещая точку 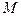 на забой центральной скважины, определим
на забой центральной скважины, определим 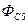 :
:
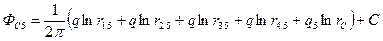 (IV.31)
(IV.31)
Вычитая из (IV.28) (IV.31) и учитывая, что
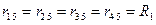
получим
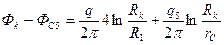
Подставив в (IV.30) и (IV.31) исходные данные
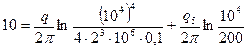
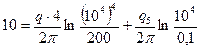
и решив полученную систему уравнений относительно 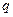 и
и 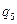 найдем
найдем
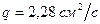 ,
, 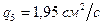
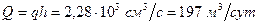
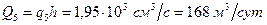
Задача 39
Круговой нефтяной пласт радиусом Rk =15 км, мощностью h = 8м эксплуатируется пятью скважинами радиусом rc =7,5 см, из которых четыре расположены в вершинах квадрата со стороной d = 150 м, а пятая — в центре (см. рис. 18). Контурное давление рk = 10,78 МПа (110 кгс/см2), скважины работают с одинаковым забойным давлением рс = 8,82 МПа (90 кгс/см2).
Коэффициент проницаемости пласта k = 0,6 Д, динамический коэффициент вязкости нефти μ = 1,1 мПа·с
Определить дебиты скважин и отношение дебитов Q5/Q1.
Ответ: Q1 = 161 м3/сут; Q5 =130 м3/сут; Q5/Q1 = 0,812.
Задача 40
Найти значения потенциалов на скважинах, расположенных снмметричнр на расстоянии 2σ = 300 м относительно центра кругового контура питания радиуса Rk = 5 км, если известно, что дебит одной составляет 200 т/сут, а другой — 300 т/сут, потенциал на контуре питания Фk = 50 см2/с, радиус скважины rс = 0,1 м, мощность пласта h = 10 м, плотность нефти ρ = 850 кг/м3.
Указание. Считать, что контур питания одинаково удален от каждой из интерферирующих скважин.
Ответ: ФC1 = 43,5 см2/с; ФC2 = 41,8 см2/с
Задача 41
Определить, при каком постоянном забойном давлении работала скв. 1 с радиусом гс = 0,1 м в круговом пласте радиуса Rk=10 км, если при введении скв. 2 с таким же радиусом, расположенной на расстоянии 2σ = 150 м от первой и работающей сзабойным давлением pc2 = 6,82 МПа (70 кгс/см2), скв. 1 была полностью заглушена. Давление на контуре питания рk = 9,8 МПа (100 кгс/см2).
Решение. Считая скважины достаточно удаленными от контура питания и применяя принцип суперпозиции, запишем выражение для потенциала результирующего течения в произвольной точке М (рис. 19).
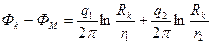
Помещая точку М на контур первой скважины, получим
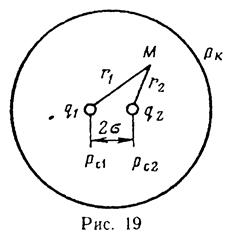
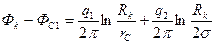
помещая ее на контур второй скважины, найдем
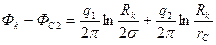
Так как скв.1 полностью заглушена, то ее дебит 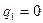 и уравнения приобретают вид
и уравнения приобретают вид
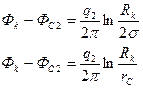
отсюда, исключая дебит 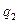 определим потенциал
определим потенциал 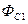 .
.
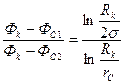
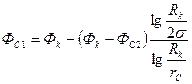
Переходя от потенциалов к давлениям, окончательно найдём
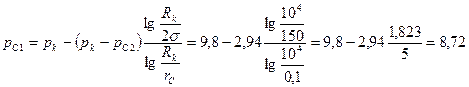 МПа
МПа
Задача 42
Совершенная скважина расположена в водяном пласте вблизи прямолинейного контура питания. Разность статического и динамического уровней ∆H = 8 м, коэффициент проницаемости k = 2Д, динамический коэффициент вязкости μ =1 сП, радиус скважины
rc = 10см и мощность пласта h = 12 м. Найти дебит скважины при двух значениях расстояния от контура питания до скважины: 1) a = 100 м, 2) а = 200 м. Представить графически расположение изобар для случая 1) при условии, что статический уровень
Hk = 40 м.
Решение. Дебит скважины вблизи прямолинейного контура питания определяется по формуле
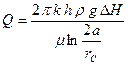
В случае 1)
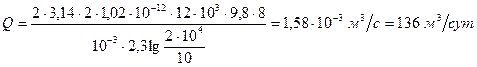
В случае 2)
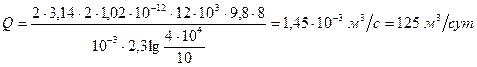
Используя метод отображения источников и стоков, получим результирующий потенциал в точке
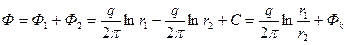
Переходя от потенциала к давлению и заменяя
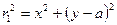 ,
, 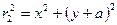
получим закон распределения давления
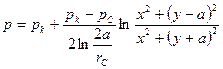
откуда найдём уравнение изобары
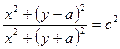
или
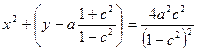
т.е. изобары представляют собой окружности с радиусом 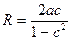 и центрами в точках с координатами
и центрами в точках с координатами 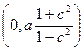
 Для построения изобар найдем давления на контуре питания и на забое скважины
Для построения изобар найдем давления на контуре питания и на забое скважины
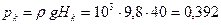 МПа
МПа
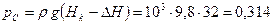 МПа
МПа
И представим уравнение изобары в виде
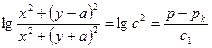
где
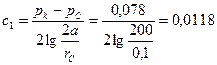 МПа
МПа
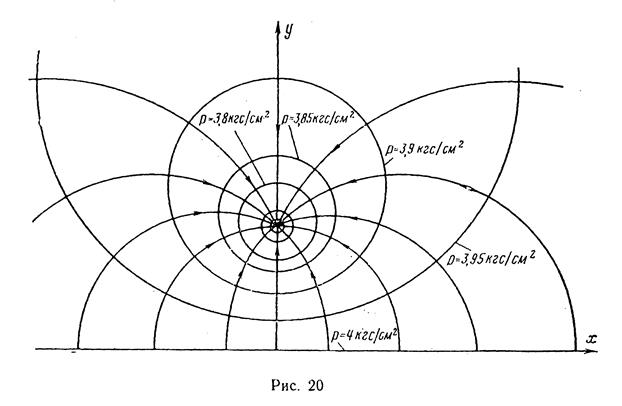
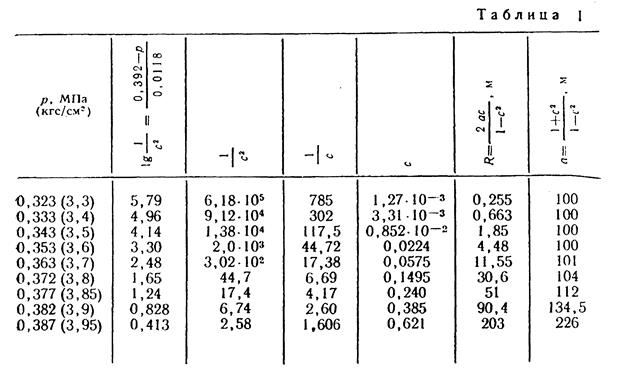
Построим изобары с давлениями 0,323 МПа (3,3 кгс/см2); 0,333 (3,4); 0,343 (3,5); 0,353 (3,6); 0,363 (3,7); 0,372 (3,8); 0,377 (3,85); 0,382 (3,9); 0,387 (3,95). Для этих давлений определим 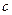 ,
, 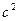 , R (табл. 1) и координаты центров изобар (рис. 20).
, R (табл. 1) и координаты центров изобар (рис. 20).
 Задача 43
Задача 43
Назовем эффектом взаимодействия Е отношение суммарного дебита всех интерферирующих скважин к суммарному дебиту того же числа скважин без учета их взаимодействия.
Найти изменение эффекта взаимодействия в зависимости от числа скважин, эксплуатирующих залежь радиусом Rk = 5000 м; радиус скважины rс =10 см; скважины работают при постоянной депрессии.
Сопоставить следующие случаи:
а) две скважины находятся ка расстоянии d = 100 м;
б) три скважины расположены в вершинах равностороннего треугольника со стороной d= 100 м;
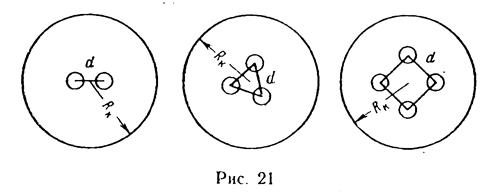
в) четыре скважины — в вершинах квадрата со стороной d = 100 м (рис. 21).
Решение. Считая, что скважины расположены равномерно по окружности, концентричной с контуром питания, используем формулу дебита одной скважины круговой батареи
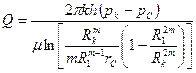
которую можно упростить в условиях рассматриваемой задачи, так как 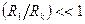 , и представить в виде
, и представить в виде
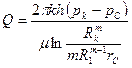
Дебит одиночной скважины в круговом пласте определяется по формуле Дюпюи
Дебит одиночной скважины в круговом пласте определяется по формуле Дюпюи
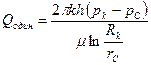
Эффект взаимодействия равен
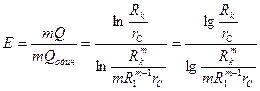
В случае а)
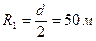 ,
, 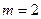
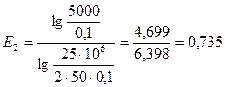
б) радиус батареи из трех скважин 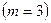 , расстояние между которыми
, расстояние между которыми 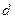 , равен
, равен 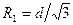 ; в этом случае
; в этом случае
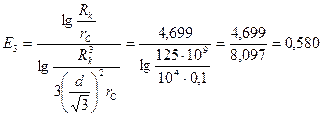
в) радиус батареи из четырех скважин, расположенных в вершинах квадрата со стороной 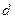 ,составляет
,составляет 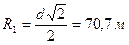 .
.
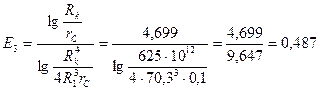
По полученным данным, и учитывая, что при 
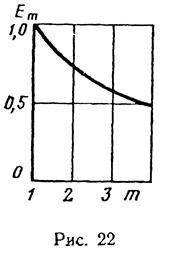
 , построим график изменения эффекта взаимодействия Ет в зависимости от числа скважин т (рис. 22).
, построим график изменения эффекта взаимодействия Ет в зависимости от числа скважин т (рис. 22).
Задача 44
В круговом пласте радиуса Rk = 200 м работает эксцентрично расположенная скважина радиусом rс =10 см (рис. 23).
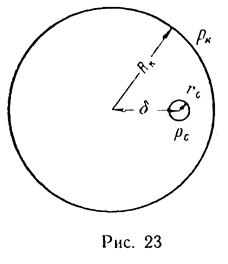
Найти изменение дебита в зависимости от расположения скважины (эксцентриситета δ) по отношению к дебиту скважины, расположенной в центре.
Решение. Дебит эксцентрично расположенной скважины определяется по формуле
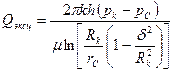
Отношение 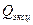 к
к
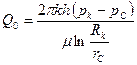
равно
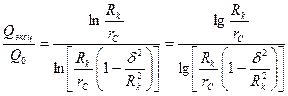
Значения 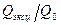 в зависимости от
в зависимости от 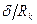 приведены ниже:
приведены ниже:
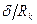 ……………0,1 0,3 0,5 0,7 0,8 0,9 0,98
……………0,1 0,3 0,5 0,7 0,8 0,9 0,98
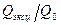 ………1,000 1,013 1,038 1,097 1,153 1,280 1,735
………1,000 1,013 1,038 1,097 1,153 1,280 1,735
Задача 45
В круговом пласте радиуса Rk = 150 м с мощностью h = 10 м и коэффициентом проницаемости k = 0,5 Д расположена скважина радиусом rc = 10 см. При ∆ p = рk — рс = 1,18 МПа (12 кгc/см2) дебит нефти с динамическим коэффициентом вязкости μ = 2 мПа·с при центральном расположении скважины равен 223 м3/сут.
 Как необходимо изменять депрессию∆ p,чтобы при изменении положения скважины относительно центра пласта дебит оставался постоянным?
Как необходимо изменять депрессию∆ p,чтобы при изменении положения скважины относительно центра пласта дебит оставался постоянным?
Решение. Из формулы дебита эксцентрично расположенной скважины выразим депрессию
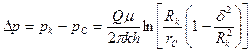
и подставим данные задачи
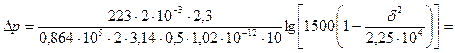
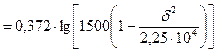 МПа
МПа
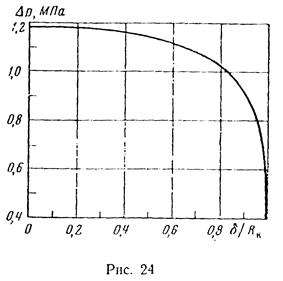
В зависимости от различных значений эксцентриситета δ получаем соответствующие значения депрессии ∆ р (рис.24).
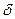 , м…………… 0 15 30 45 60 75
, м…………… 0 15 30 45 60 75
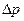 , МПа……… 1,180 1,180 1,173 1,166 1,151 1,134
, МПа……… 1,180 1,180 1,173 1,166 1,151 1,134
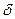 , м……………………… 90 105 120 135 149
, м……………………… 90 105 120 135 149
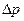 , МПа………………… 1,107 1,071 1,015 0,912 0,483
, МПа………………… 1,107 1,071 1,015 0,912 0,483
Задача 46
Вывести формулу дебита скважины круговой батареи радиуса R, состоящей из т скважин, расположенной в центре кругового пласта радиуса Rk, концентрично контуру питания.
Подсчитать дебит при следующих данных: R = 150 м, т = 6, Rк = 3000 м, rc = 0,1 м, рk= 11,76 МПа (120 кгс/см2), рс = 9,8 МПа (100 кгс/см2), коэффициент проницаемости k = 0,2 Д, мощность пласта h = 10 м, динамический коэффициент вязкости нефти μ = 2 мПа·с. Сравнить дебит одной скважины батареи с дебитом одной скважины в центре пласта.
Решение. Используя принцип суперпозиции, запишем результирующий потенциал на забое первой скважины
 (IV.32)
(IV.32)
где r1j — расстояние между центрами первой и j-той скважин. Как видно из чертежа (см. рис. 13),
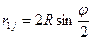 (IV.33)
(IV.33)
где
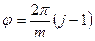
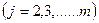
Потенциал на контуре питания
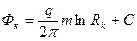 (IV.34)
(IV.34)
вычтем из (IV.34) (IV.32), получим
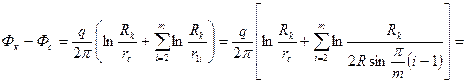
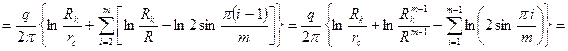
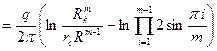 (IV.35)
(IV.35)
Преобразуем выражение
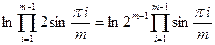 (IV.36)
(IV.36)
Известно (5), что
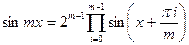
Выделив первый сомножитель, равный sin x, из произведения и разделив на него правую и левую части равенства, получим
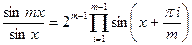
При 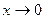 левая часть принимает значение т, поэтому
левая часть принимает значение т, поэтому
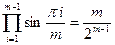 (IV.37)
(IV.37)
Подставляя (IV.37) в (IV.35), учитывая (IV.36), найдем
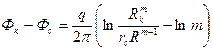
откуда
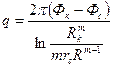
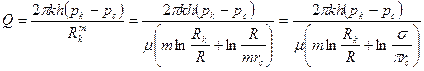
Подставляя исходные данные, получим

Дебит отдельной скважины, расположенной в центре пласта, составлял бы
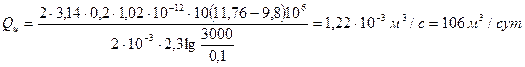
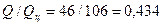
Задача 47
Определить дебиты скважин двух круговых батарей с радиусами R 1 = 1000 м и R2 = 600 м, расположенных концентрично в круговом пласте с радиусом контура питания Rk = 3500 м. Скважины радиусом rc = 10 см эксплуатируются при постоянных забойных давлениях pc1 = 9,8 МПа (100 кгс/см2), рс2 = 9,31 МПа (95 ктс/см2), давление на контуре питания рк = 12,25 МПа (125 кгс/см2), мощность пласта h = 10м, коэффициент проницаемости пласта k = 0,2 Д, динамический коэффициент вязкости нефти μ = 5 мПа·с. Число скважин в батареях m1= 10, m2 =6.
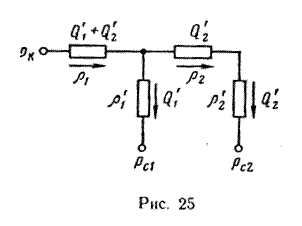
Решение. Используя метод Ю. П. Борисова, составим схему эквивалентных фильтрационных сопротивлений (рис. 25).
Определим внешние и внутренние фильтрационные сопротивления:
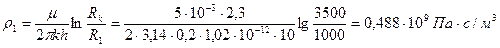
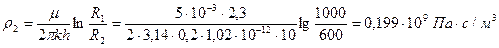
Для определения внутренних фильтрационных сопротивлений найдем половины расстояний между скважинами первой и второй батарей
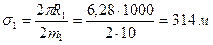
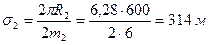
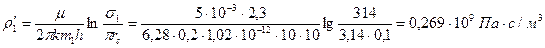
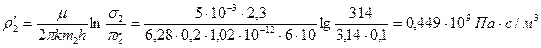
Используя законы Ома и Кирхгофа, напишем уравнение для участка цепи между контуром питания и забоем скважины первой батареи
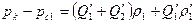
и аналогично между контуром питания и забоем скважины второй батареи
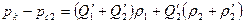
В полученную систему уравнений подставим данные
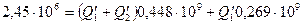
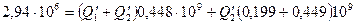
решая уравнения относительно 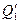 и
и 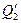 , найдем
, найдем

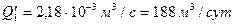
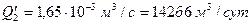
Учитывая, что 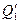 и
и 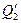 — суммарные дебиты первой и второй батарей, найдем дебиты одной скважины
— суммарные дебиты первой и второй батарей, найдем дебиты одной скважины
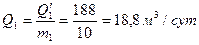
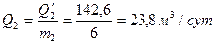
Задача 48
Определить дебиты скважин, расположенных тремя кольцевыми батареями. Давление иа контуре питания рк =16,7 МПа, забойные давления на всех эксплуатационных скважинах одинаковы и равны 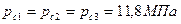 . Радиусы батарей R1 = 4000 м, R2 = 3500 м, R3 = 3000 м. Радиус скважин
. Радиусы батарей R1 = 4000 м, R2 = 3500 м, R3 = 3000 м. Радиус скважин 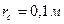 , радиус контура области питания Rk = 20 км. Расстояние между скважинами в батареях
, радиус контура области питания Rk = 20 км. Расстояние между скважинами в батареях 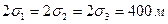 , мощность пласта h = 10 м, коэффициент проницаемости k = 1Д, динамический коэффициент вязкости нефти μ = 3 мПа·с.
, мощность пласта h = 10 м, коэффициент проницаемости k = 1Д, динамический коэффициент вязкости нефти μ = 3 мПа·с.
Указание. Задачу решать методом эквивалентных фильтрационных сопротивлений Ю. П. Борисова.
Ответ: Q1 = 57,9 м3/сут; Q2 = 22,2 м3/сут; Q3 =10,4 м3/сут.
Задача 49
Определить забойные давления скважин, расположенных в круговом пласте радиуса Rk = 10 км двумя концентричными кольцевыми батареями с радиусами R1 = 2000 м, R2 = 1200 м. Число скважин в батареях т1 = 30, т 2=16; дебит одной скважины первой батареи Q1 = 80 м3/сут, второй — Q2 = 70 м3/сут; радиус скважины rс = 10 см, мощность пласта h =15 м, кэффициент проницаемости пласта k = 0,8 Д, динамический коэффициент вязкости жидкости μ = 8 сП, давление на контуре питания пласта рк =14,7 МПа (150 кгс/см2).
Ответ: рс, = 11,9 МПа (121,5 кгс/см2); рс2 =11,7 МПа (119,1 кгс/см2).
Задача 50
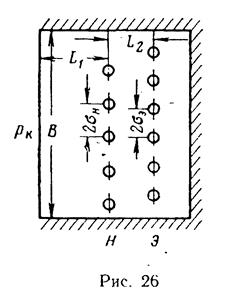
В полосообразной залежи имеется один ряд эксплуатационных и один ряд нагнетательных скважин, расположенный между контуром питания и эксплуатационными скважинами (рис. 26). Определить необходимое количество нагнетаемой жидкости 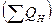 , давление нагнетания рн и утечку жидкости за контур питания
, давление нагнетания рн и утечку жидкости за контур питания 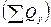 (или количество поступающей жидкости от контура питания), чтобы суммарный дебит эксплуатационных скважин составлял
(или количество поступающей жидкости от контура питания), чтобы суммарный дебит эксплуатационных скважин составлял 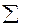 Qэ =1000 м3/сут. Ширина залежи равна В = 5000 м, мощность пласта h = 10 м, расстояниеот контура питания до ряда нагнетательных скважин L1 = 1500 м, расстояние между рядами скважин L2 = 600 м, расстояние между нагнетательными скважинами 2 σH = 300 м, между эксплуатационными скважинами 2 σэ = 400 м; все скважины гидродинамически несовершенны, приведенный радиус составляет r'с =0,1 см, давление на контуре питания рк = 11,76 МПа (120 кгс/см2), давление па забое эксплуатационных скважин рс = 7,84 МПа (80 кгс/см2), коэффициент проницаемости пласта k = 0,5Д, динамический коэффициент вязкости нефти μ = 4мПа·с.
Qэ =1000 м3/сут. Ширина залежи равна В = 5000 м, мощность пласта h = 10 м, расстояниеот контура питания до ряда нагнетательных скважин L1 = 1500 м, расстояние между рядами скважин L2 = 600 м, расстояние между нагнетательными скважинами 2 σH = 300 м, между эксплуатационными скважинами 2 σэ = 400 м; все скважины гидродинамически несовершенны, приведенный радиус составляет r'с =0,1 см, давление на контуре питания рк = 11,76 МПа (120 кгс/см2), давление па забое эксплуатационных скважин рс = 7,84 МПа (80 кгс/см2), коэффициент проницаемости пласта k = 0,5Д, динамический коэффициент вязкости нефти μ = 4мПа·с.
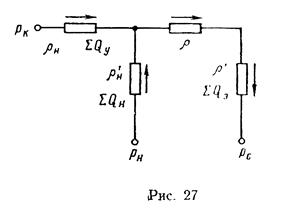
Решение. Составим схему фильтрационных сопротивлений, отвечающую нашей задаче (рис. 27), и найдем фильтрационные сопротивления, проводя расчет для суммарных дебитов рядов.
Внешние сопротивления равны:
между контуром питания и нагнетательным рядом
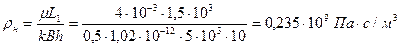
между рядами скважин
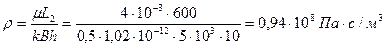
Для определения внутренних сопротивлений найдем число эксплуатационных (тэ) и нагнетательных (тн) скважин:
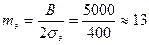
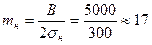
точка
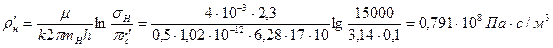
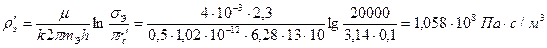
Согласно законам Кирхгофа, считая, что жидкость поступает в пласт от контура, составим уравнения:
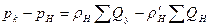
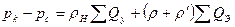
кроме того
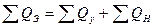
Из второго уравнения находим
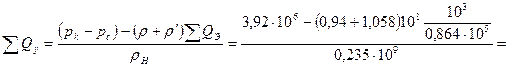
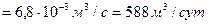
из третьего — закачиваемый дебит
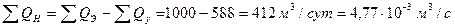
а из первого — давление нагнетания рн
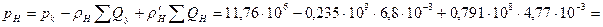
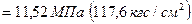
Так как 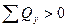 , то в действительности имеет место приток жидкости в пласт, а не утечка за контур питания.
, то в действительности имеет место приток жидкости в пласт, а не утечка за контур питания.
Задача 51
Используя данные предыдущей задачи, определить давление нагнетания 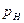 количество нагнетаемой жидкости
количество нагнетаемой жидкости 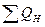 и величину утечки за контур питания
и величину утечки за контур питания 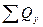 , если поменять местами ряды эксплуатационных и нагнетательных скважин (т. е. рассмотреть случай заводнения со стороны непроницаемой границы) и принять давление на контуре питания рк = 9,8 МПа (100 кгс/см2).
, если поменять местами ряды эксплуатационных и нагнетательных скважин (т. е. рассмотреть случай заводнения со стороны непроницаемой границы) и принять давление на контуре питания рк = 9,8 МПа (100 кгс/см2).
Ответ: рн= 10,19 МПа (104 кгс/см2); 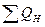 = 619 м3/сут;
= 619 м3/сут; 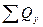 = 383 м3/сут.
= 383 м3/сут.
Задача 52
Совершенная скважина радиуса rс = 10 см работает в пласте, ограниченном двумя прямолинейными непроницаемыми границами, расположенными под утлом 90° друг к другу (рис. 28). Расстояния до границ равны а =150 м, b = 300 м, расстояние до контура питания Rk = 8,0 км. Давление на контуре питания pk= 11,76 МПа (120 кгс/см2), давление на забое скважины pc = 9,8 МПа (100 кгс/см2), мощность пласта h=12 м, динамический коэффициент вязкости жидкости μ = 3 мПа·с, коэффициент проницаемости k = 700мД. Найти дебит скважины.
Решение. Продолжим непроницаемые границы вверх и влево до кругового контура питания радиусом Rк и отобразим скважину-сток относительно них без изменения знака дебита. В результате отображения получим в круговом пласте четыре скважины-стока, из которых одна — реальная и три — фиктивные. При этом гидродинамическая картина течения в пласте при отсутствии непроницаемых границ при одновременной работе четырех скважин-стоков будет совпадать с гидродннамической картиной при наличии непроницаемых границ, так как эти границы являются линиями тока. Считая, что контур питания расположен на достаточно большом расстоянии от скважин, результирующий потенциал в некоторой точке пласта можно записать в виде суммы потенциалов, возбуждаемых каждым стоком в неограниченном пласте,
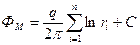
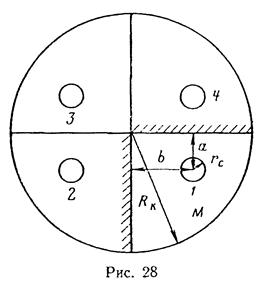
Поместим точку М на контур скважины, тогда
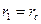
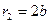
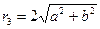
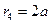
Помещая точку М на контур питания, получим

а вычитая, найдем
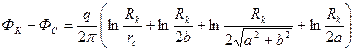
откуда
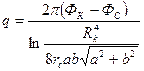
или
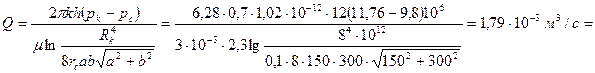
Задача 53
Определить дебит скважины, работающей в пласте, ограниченном двумя прямолинейными непроницаемыми границами, расположенными под углом 60° друг к другу. Расстояние от точки пересечения непроницаемых границ до скважины r =200 м, расстояние до одной из границ а = 50 м, радиус контура питания Rk = 5 км (рис. 29). Мощность пласта h = 10 м, коэффициент проницаемости пласта k = 0,3 Д, динамический коэффициент вязкости жидкости μ = 2 мПа·с, депрессия ∆р = = 2,45 МПа (25 кгс/см2), радиус скважины rс =0,1 м.
Решение. Продолжим непроницаемые границы и отобразим реальную скважину-сток относительно границ, сохраняя для дебита тот же знак. В результате получим два стока-изображения— № 2 и № б: появление стока-изображения № 6 нарушает условие непроницаемости границы ОА, а наличие стока № 2 нарушает условие на границе ОB, поэтому их надо в свою очередь отразить: №6 - относительно границы ОА, № 2 — относительно ОВ. При этом появляются стоки-изображения № 3 и № 5, из которых № 3 нарушает непроницаемость границы  а № 5 - границы
а № 5 - границы 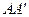 их изображения относительно этих границ совпадают и дают сток-изображение № 4.
их изображения относительно этих границ совпадают и дают сток-изображение № 4.
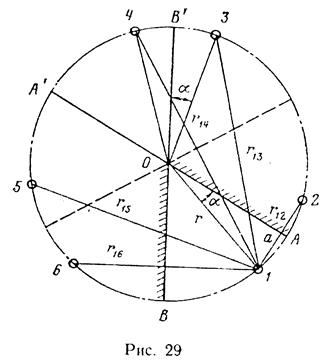 Таким образом, задача о фильтрации в клине сводится к задаче о фильтрации в круговом пласте радиуса Rk, в котором работают одновременно реальная скважина-сток и пять стоков-изображений, расположенных по окружности радиуса r.
Таким образом, задача о фильтрации в клине сводится к задаче о фильтрации в круговом пласте радиуса Rk, в котором работают одновременно реальная скважина-сток и пять стоков-изображений, расположенных по окружности радиуса r.
Применяя принцип суперпозиции, запишем результирующий потенциал на забое реальной скважины:

где
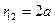 ,
, 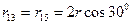 ,
, 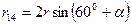
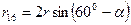
а угол α определяется из соотношения sin α = а / r = 0,25, α = 14°30' (см. рис. 29).
Потенциал на контуре питания, который считаем удаленным от группы взаимодействующих скважин, получим в виде
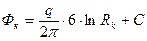
разность потенциалов
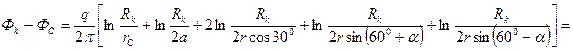
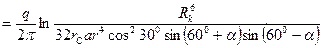
откуда
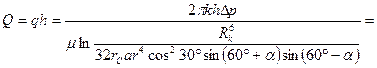
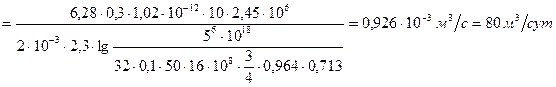
Задача 54
В пласте с эллиптическим контуром питания работает прямолинейная цепочка, составленная из m = 10 равноотстоящих друг от друга скважин радиусом rс = 0,1 м. Расстояние между соседними скважинами цепочки 2σ = 300 м. Минимальное расстояние от центра залежи до контура питания (малая полуось эллипса) L = 5 км. Мощность пласта h = 10 м, коэффициент проницаемости k = 800 мД, динамический коэффициент вязкости жидкости µ = ЗмПа•с, давление на контуре питания рк = 11,76 МПа (120 кгс/см2), давление на забое скважин рс = 9,8 МПа (100 кгс/см2). В пласте имеет место установившаяся фильтрация однородной жидкости по закону Дарси.
Определить дебиты крайних и центральных скважин и сопоставить их с дебитом скважины бесконечной прямолинейной цепочки.
Решение. Дебит одной скважины конечной прямолинейной цепочки в эллиптическом пласте определяется по формуле В.Т.Мироненко.
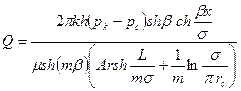
где β находится из уравнения
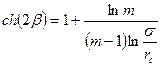
х — координата центра скважины (см. рис. 14).
Подставляя данные задачи, найдем
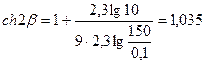
откуда 2β = 0,246, β = 0,132,
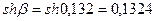 ,
, 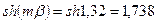
Для определения 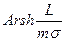 — воспользуемся формулой
— воспользуемся формулой
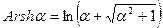
и получим
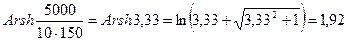
Для центральных скважин x1 = ± 150 м, поэтому
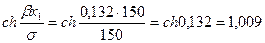
и дебит
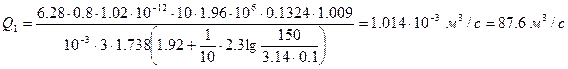
Для крайних скважин 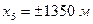 , поэтому
, поэтому
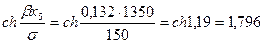
и дебит равен
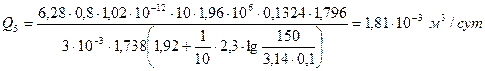
Дебит одной скважины бесконечной цепочки в пласте с двусторонним контуром питания, расположенным на расстоянии L=5 км от цепочки, определяется по формуле
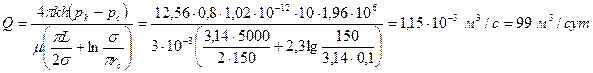
Задача 55
Определить, каким плоским фильтрационным потокам соответствуют следующие характеристические функции (комплексные потенциалы):
1. 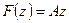
2. 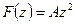
3. 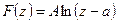
4. 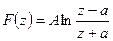
где А и а — действительные постоянные числа.
Решение. Вкачестве примера рассмотрим случаи 2 и 4. Для этих случаев найдем потенциалы скорости фильтрации и функции тока, уравнения изобар и линий тока, модули скоростей фильтрации и построим семейства изобар и линий тока. Для случая 2.

Приравнивая действительную часть потенциалу скорости фильтрации Ф, а мнимую часть — функции тока Ψ, получим
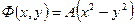
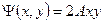
Уравнение семейства эквипотенциалей получим, полагая
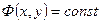
т.е.
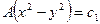 (IV.38)
(IV.38)
а уравнение семейства линий тока, полагая
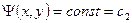
т.е.
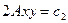 (IV.39)
(IV.39)
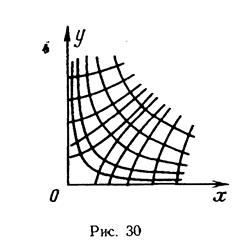
Уравнение (IV.38) определяет собой семейство гипербол, асимптотами которых являются биссектрисы координатных углов, а уравнение (IV.39)—семейство гипербол с асимптотами, совпадающими с осями координат (рис. 30).
Найдем составляющие скорости фильтрации wx и 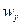 :
:
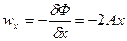
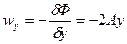
и модуль скорости фильтрации
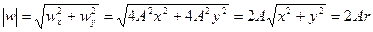
Представим для случая 4 комплексные числа z — а и z + a: в полярных координатах (см. рис. 31):
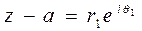
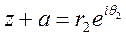
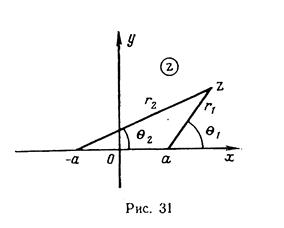
Тогда комплексный потенциал
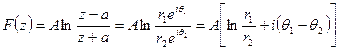
Отсюда
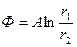
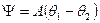
и уравнения семейства эквипотенциалей и линий тока можно записать в виде
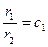
или
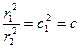 (IV.40)
(IV.40)
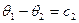 (IV.41)
(IV.41)
Перейдем к декартовым координатам и определим, какие кривые описываются уравнениями (IV.40) и (IV.41). Как видно из чертежа (см. рис. 31),
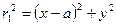
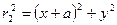
и уравнение (IV.40) принимает вид
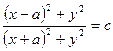
или
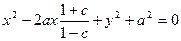
Дополняя первые два слагаемых до квадрата разности, получим
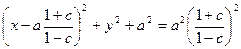
или
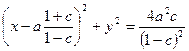
что является уравнением окружности с центром в точке с координатами
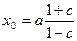 ,
, 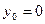
и радиус 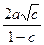
Как видно из чертежа,
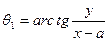
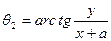
что после подстановки в уравнение (IV.41) дает
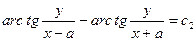
Используя формулу тангенса разности двух углов, запишем
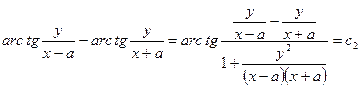
или
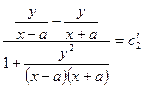
Последнее уравнение можно привести к виду
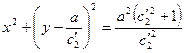
откуда видно, что оно описывает окружность с центром 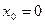 ,
,  и радиусом
и радиусом
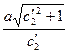
Если нанести на рисунок эквипотенциали и линии тока (рис. 32), то можно увидеть, что данная характеристическая функция
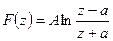
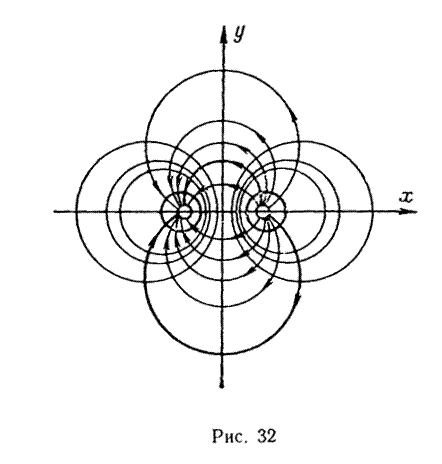
соответствует фильтрационному потоку в неограниченной плоскости при наличии источника и стока, расположенных на оси х в точках с координатами + а и — а.
Модуль скорости фильтрации определим по формуле
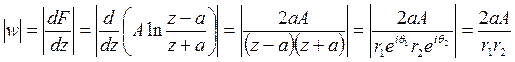
Задача 56
Эксплуатационная скважина работает в пласте, в котором до ее пробуривания имелся напорный плоскопараллельный поток жидкости со скоростью фильтрации w = 0,001 см/с.
Дебит скважины 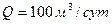 , мощность пласта h=10 м. Изобразить графически линии тока результирующего течения.
, мощность пласта h=10 м. Изобразить графически линии тока результирующего течения.
Решение. Используя принцип суперпозиции, запишем характеристическую функцию для фильтрационного потока как сумму характеристической функции, отвечающей плоскопараллельному потоку в направлении оси х и равной (—wz), и характеристической функции плоскорадиального потока со стоком в начале координат 
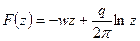
Представляя комплексную переменную z в декартовых и полярных координатах
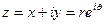
отделим действительную часть от мнимой
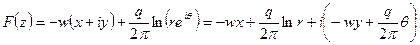
и запишем выражение для функции тока
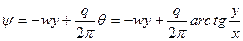
Уравнение линий тока имеет вид
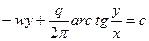
Подставляя исходные данные в системе СГС, получим
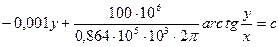
или
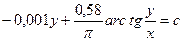
Запишем последнее уравнение в виде
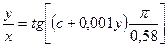
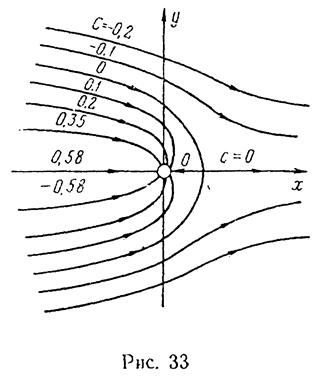
Рассчитаем несколько линий тока, придавая постоянной с различные значения. Результаты расчетов сведены в табл. 2 и представлены на рис. 33.
Значению 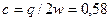 соответствует линия тока
соответствует линия тока 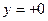 ,
, 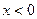 . В нижней полуплоскости картина линий тока симметрична относительно оси х, только соответствующие линии тока характеризуются значениями с с обратными знаками.
. В нижней полуплоскости картина линий тока симметрична относительно оси х, только соответствующие линии тока характеризуются значениями с с обратными знаками.

Как видно из графика, линия тока со значением с = 0 является нейтральной линией, ограничивающей область засасывания, т. е. область, в которой жидкость поглощается скважиной. Наибольшая ширина области засасывания равна