При больших давлениях уравнение состояния реального газа отличается от уравнения Клапейрона и имеет вид
 (VIII.27)
(VIII.27)
где z = z(pr, Tr) — коэффициент сверхсжимаемости газа, учитывающий отклонение реального газа от идеального и зависящий от приведенных давления и температуры


и определяемый по графику (рис. 55). Здесь 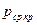 и
и  — соответственно среднекритическое давление и среднекритнчеcкая температура. Так как природный газ состоит из различных компонентов (метан, этан, пропан и др.). то предварительно нужно вычислить значения
— соответственно среднекритическое давление и среднекритнчеcкая температура. Так как природный газ состоит из различных компонентов (метан, этан, пропан и др.). то предварительно нужно вычислить значения 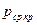 и
и  по формулам
по формулам


где nj — содержание j -го компонента в газе, об. %;  и
и  — критическое давление и температура j -го компонента соответственно.
— критическое давление и температура j -го компонента соответственно.
Динамический коэффициент вязкости природного (реального) газа зависит от давления и температуры. Считая процесс изотермическим, нужно учитывать зависимость µ(p). На основании экспериментальных исследований построены графики, по которым с точностью до 6% можно найти значения дмнамического коэффициента вязкости природного газа при различных давлениях и температурах в зависимости от относительной плотности по воздуху (рис. 56).
Для определения массового дебита реального газа или закона распределения давления нужно записать закон Дарси для бесконечно малого элемента пласта и, учитывая зависимость µ (р) и формулу (VIII.27), проинтегрировать его графоаналитическим методом (см. задачи 83, 84). Если давление в пласте меняется в небольшом интервале, то можно аппроксимировать зависимость p/µ(p)z(p) простой алгебраической функцией, взять интеграл аналитически и получить аналитическое выражение для дебита и закона распределения давления.

Задача 75
Определить проницаемость песка, если через трубу диаметром d = 200 мм и длиной l = 12 м, заполненную этим песком, пропускался воздух вязкостью 0,018 мПа•с при перепаде давления, равном 4,41•104 Па (0,45 кгс/см2); избыточные давления в начале и в конце трубы составляют p1 =0,98•105 Па (1 кгс/см2), р2 = 0,539•105 Па (0,55 кгс/см2). Средний расход воздуха, приведенный к атмосферному давлению, равен 250 см3/с. Атмосферное давление принять равным рат = 0,98•105 Па, температуру t = 20°C.
Ответ: k = 21,5 Д.

Задача 76
Сравнить распределение давления в пласте в случаях установившейся плоскорадиалыюй фильтрации газа и несжимаемой жидкости по закону Дарси при одинаковых граничных условиях: rс = 0,1 м, рс = 50 кгс/см2, Rк = 750 м, рк=100 кгс/см2.
Решение. Определим, какая часть (в процентах) депрессии  теряется при движении несжимаемой жидкости и газа в пласте на расстоянии r—rс.
теряется при движении несжимаемой жидкости и газа в пласте на расстоянии r—rс.

Из закона распределения давления в несжимаемой жидкости

получим

Из закона распределения давления газа

найдем

Задаваясь различными значениями  , подсчитаем δж и δг и результаты представим на рис. 57 и ниже.
, подсчитаем δж и δг и результаты представим на рис. 57 и ниже.


Задача 77
В пласте имеет место установившаяся плоскорадиальная фильтрация газа по закону Дарси. Абсолютное давление на контуре питания рк = 9,8 МПа (100 кгс/см2), давление на забое скважины рс = 6,86 МПа (70 кгс/см2), приведенный к атмосферному давлению и пластовой температуре объемный расход газа Qат = 8·105 м3/сут. Радиус контура питания Rk = 750 м, радиус скважины rс = 0,1 м, мощность пласта h = 10 м, пористость m = 20%. Определить давление, скорость фильтрации и среднюю скорость движения газа на расстоянии r = 50 м от скважины.
Ответ: р = 9,02 МПа; w = 3,32·10-5 м/с; v = 1,66·10-4 м/с.
Задача 78
Определить расстояние 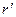 от возмущающей газовой скважины до точки пласта, в которой давление равно среднеарифметическому от забойного давления рс = 70 кгс/см2 и давления на контуре питания pk =100 кгс/см2. Расстояние до контура питания Rk = 1000 м, радиус скважины rc =10 см.
от возмущающей газовой скважины до точки пласта, в которой давление равно среднеарифметическому от забойного давления рс = 70 кгс/см2 и давления на контуре питания pk =100 кгс/см2. Расстояние до контура питания Rk = 1000 м, радиус скважины rc =10 см.
Ответ: 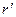 = 6,76 м.
= 6,76 м.
3адача 79
Определить объемный приведенный к атмосферному давлению и массовый дебиты совершенной газовой скважины, считая, что фильтрация происходит по закону Дарси, если мощность пласта h = 25 м, коэффициент проницаемости пласта k = 250 мД, динамический коэффициент вязкости газа μ = 0,014 мПа·с, плотность газа в нормальных условиях ρат = 0,650 кг/м3, радиус скважины rc = 0,1 м расстояние до контура питания Rк = 900 м, абсолютные давления на забое скважины рс = 2,94 МПа и на контуре питания рк = 3,92 МПа, газ считать идеальным.
Ответ: Qm = 607 т/сут; Qат = 0,935·106 м3/сут.
Задача 80
Известно, что в пласте происходит установившаяся плоскорадиальная фильтрация газа по закону Дарси. Радиус контура питания Rk = 1000м, радиус скважины rс = 0,1 м, абсолютное давление газа на контуре питания рк =100 кгс/см2, давление на забое скважины рс = 92 кгс/см2. Определить средневзвешенное по объему пласта давление  .
.
Решение. При установившейся плоскорадиальной фильтрации газа по закону Дарси давление в каждой точке пласта определяется по формуле

Для нахождения средневзвешенного пластового давления газа  выделим на расстоянии r от скважины кольцевой элемент пласта шириной dr. Объем порового пространства этого элемента равен
выделим на расстоянии r от скважины кольцевой элемент пласта шириной dr. Объем порового пространства этого элемента равен

Объем порового пространства всего пласта равен

Давление


Если правую и левую части полученного равенства разделим на pk и введем обозначения  и
и  , то получим
, то получим

Заменим
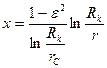
тогда

Если |x|<1, то  можно разложить в ряд.
можно разложить в ряд.
Известно, что

Разложим  в ряд, удержав первые два члена ряда.
в ряд, удержав первые два члена ряда.

Тогда

Интегрируя, подставляя пределы и пренебрегая членами, содержащими  ,получим
,получим

Подсчитаем среднее пластовое давление по данным задачи

откуда 
Как видно, при установившейся плоскорадиальной фильтрации газа средневзвешенное пластовое давление  близко к контурному давлению
близко к контурному давлению  .
.
Задача 81
Показать, что при установившемся прямолинейно-параллельном движении газа в пористой среде в условиях напорного режима распределение давления в пласте не описывается законом фильтрации, выраженным в виде одночленной степенной формулы вида (II.11).
Решение. Из принципа однородности размерностей следует, что
 ,
,
где x —координата, взятая вдоль линии тока по движению газа. Отсюда массовый расход
 .
.
Обозначив

и введя функцию Лейбензона
 ,
,
Получим дифференциальное уравнение
 ,
,
откуда
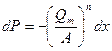 .
.
Проинтегрировав полученное уравнение с учетом граничных условий
x=0; P=P к; x=l; P=P г;
 ,
,
получим
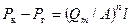 ,
,
откуда
.
Интегрируя по х от 0 до х и по Р от Рк до Р, получим

 ,
,
или
 .
.
Переходя от функции Лейбензона к давлению, получим окончательно закон распределения давления
 ,
,
не зависящий от значения п, характеризующего закон фильтрации.
Задача 82
Найти коэффициенты А и В уравнения индикаторной кривой по данным испытания газовой скважины, приведенным в табл.3.

Решение. Возьмем уравнение индикаторной линии в виде двучленной формулы (VIII.26)
 ,
,
где
 ,
,
и перепишем его в виде
 .
.
Коэффициенты А и В найдем по способу наименьших квадратов, для чего подсчитаем значения Dр2, Dp2/Qат, Q ат2и их суммы и результаты занесем в табл. 4.


 .
.

Кроме того, найдем
SQат = 5,475×105 м3/сут.
и
(SQат)2 = 29,97×1010 м6/сут2.
Обозначим через хi и yi значения Q aт и Dp2 /Qaт при i -том замере. Для каждого замера мы имеем уравнение
 . (VIII.28)
. (VIII.28)
Сложив почленно уравнения (VIII.28) для i =l, 2,..., п (где п — число испытаний), получим
 . (VIII.29)
. (VIII.29)
Умножим правую и левую части уравнения (VI 11.28) на xi

и просуммируем полученные уравнения
 . (VIII.30)
. (VIII.30)
Система уравнений (VIII.29) и (VIII.30) служит для определения неизвестных А и В, которые найдем по формулам Крамера
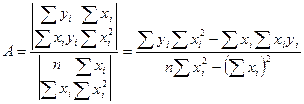 ,
,
 .
.
Учитывая, что
xi = (Q ат) i,
 ,
,
xiyi = (Dp 2) i ,
получим формулы для А и В ввиде
 ,
,

Подставляя исходные данные, найдем численные значения А и В
 ,
,
 .
.
Задача 83
Природный газ имеет следующий состав:

Определить дебит Qат газовой скважины, учитывая свойства реального газа, и сравнить его с дебитом Q' aтдля идеального газа.
При решении использовать график зависимости коэффициента сверхсжимаемости z от приведенных температуры и давления и график зависимости динамического коэффициента вязкости m от давления и плотности газа при температуре пласта t = 38° С.
Статическое давление на забое скважины, принимаемое за контурное, p к = 150 кгс/см2, динамическое — р с = 100 кгс/см2, коэффициент проницаемости k = 0,1 Д, мощность пласта h = 10 м, радиус контура области дренирования R к = 1 км, радиус: скважины r с = 10 см.
Решение. При линейной фильтрации и установившемся движении газа массовый дебит скважины определяется по формуле-Дарси
 . (VIII.31)
. (VIII.31)
Интегрируя и учитывая, что r и m являются функциями давления, получим
 (VIII.32)
(VIII.32)
Из уравнения состояния реального газа p/r = zRT имеем
 (VIII.33)
(VIII.33)
Подставляя в интеграл (VIII. 32) выражение (VI 11.33), запишем
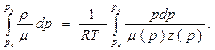
Для того чтобы найти численное значение интеграла, разбиваем диапазон изменения давления на шесть интервалов и аппроксимируем интеграл
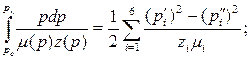 (VIII.34)
(VIII.34)
здесь pi’ и р i" —крайние значения давлений в i -том интервале; zi и mi — значения коэффициента сверхсжимаемости z(p) и динамического коэффициента вязкости m(р) при давлении рi = (рi'+ рi") / 2.
С учетом выражения (VIII.34) получим формулу для дебита в виде
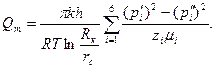 (VIII.35)
(VIII.35)
Значения zi определим из графика z = z(pr, Tr), для чего найдем приведенные давление и температуру в каждом интервале по формулам
рr = p / p ср.кр,
Т r = Т / Т ср.кр,
где
 ,
,
 ,
,
a nj — объемное (молярное) содержание j -го компонента в газе (табл. 5); Snj =100

По данным табл. 5
Р ср.кр = 45,69 кгс/см2, Тср.кр = 222,2 К,

Относительную плотность газа по воздуху определяем по данным последней графы табл. 5.

Значения m2 - найдем по графику зависимости m от относительной плотности газа  = 0,667 и от давления рi - при t = 38° С (см. рис. 56).
= 0,667 и от давления рi - при t = 38° С (см. рис. 56).
Определим члены суммы, входящей в выражение (VIII.35) •(табл. б).

Приведенный к атмосферному давлению объемный дебит реального газа равен
 .
.

Так как z ат= 1, то

Считая газ идеальным и принимая вязкость m = 0,0175 cП (значение, соответствующее среднему значению давления газа в пласте р= (100+ 150)/2= 125 кгс/см2), получим

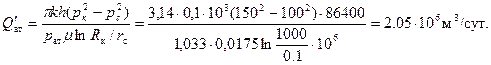
Как видно из полученных данных, в условиях рассматриваемой задачи дебит скважины с учетом реальных свойств газа больше дебита идеального газа на 28%.
Задача 84
В пласте происходит плоскорадиальная установившаяся фильтрация газа по закону Дарси. Найти распределение давления в пласте с учетом реальных свойств газа.
Состав газа приведен в условии задачи 83, давление на контуре питания рк = 150 кгс/см2, давление на забое скважины рс = 100 кгс/см2, радиус контура питания Rк = 1000 м, радиус скважины rс = 0,1 м, температура газа в пласте t = 38° С, коэффициент проницаемости пласта k = 0,1 Д, мощность пласта h = 10 м.
Решение. Для проскорадиалыюй фильтрации реального газа по закону Дарси массовый дебит равен
 (VIII.36)
(VIII.36)
Из уравнения состояния реального газа р/r = z (р, T)RT найдем зависимость r от p
 .
.
При атмосферном давлении
z (p ат, Т) = 1

Учитывая последнее равенство, найдем

Подставляя значение r в дифференциальное уравнение (Vlll.36), разделяя переменные и интегрируя по р от р до рк и по r от r до Rк, получим

или
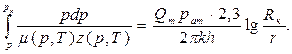 (VIII.37)
(VIII.37)
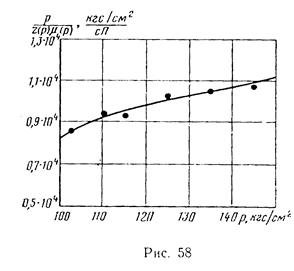
Далее решаем задачу графоаналитическим методом. Используя данные табл. 6 задачи 83, найдем значения подынтегральной функции
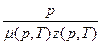
при температуре Т = 273°+38° = 311 К (табл. 7) и построим ее график (рис. 58).

Задаваясь различными значениями р (100  £ р £150
£ р £150  ), подсчитаем значения
), подсчитаем значения

как площади, заключенной между кривой, осью абсцисс и ординатами р = р и р = рк (табл. 8).


Зная из задачи 83, что Q ат = 2,83×106м3/сут = 32,75 м3/с, находим значения 
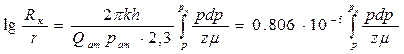
и по ним — отношения Rк/r и расстояния r (cм. табл. 8). На рис. 59 приведен график зависимости р от lg(r/rс) по данным табл. 8.
Задача 85
 Определить приведенный дебит газовой скважины, если природный газ имеет следующий состав (табл. 9).
Определить приведенный дебит газовой скважины, если природный газ имеет следующий состав (табл. 9).
Давление на контуре питания рк = 100  , давление на забое скважины рс = 50
, давление на забое скважины рс = 50  , проницаемость пласта k = 0,12 Д, мощность пласта h = 8 м, радиус контура питания Rк = 750 м, радиус скважины rс = 10 см, температура пласта t = 38° С.
, проницаемость пласта k = 0,12 Д, мощность пласта h = 8 м, радиус контура питания Rк = 750 м, радиус скважины rс = 10 см, температура пласта t = 38° С.
Указание. При решении воспользоваться методикой задачи 83.
Ответ. Qат = 1,77-106 м3/сут.
Задача 86
Совершенная скважина расположена в центре кругового пласта радиуса Rк =10 км, мощность пласта в среднем равна h = 15 м, коэффициент проницаемости k = 400 мД, коэффициент динамической вязкости пластовой жидкости m = 1,02 мПа×с, коэффициент сжимаемости жидкости bж = 4,64 • 10-10 Па-1, давление на контуре питания рк = 11,76 МПа, забойное давление рс = 7,35МПа, радиус скважины rс = 0,1 м. Фильтрация происходит при водонапорном режиме по закону Дарси.
Определить различие в объемном суточном дебите скважины, подсчитанном с учетом сжимаемости жидкости и при условии, что жидкость несжимаема.
Решение. Формулу дебита скважины с учетом сжимаемости можно получить из формулы Дюпюи, заменяя объемный расход Q расходом Qm, а давление р функцией Лейбензона Р.

Для жидкости, подчиняющейся закону Гука с уравнением состояния r =  функция Лейбензона
функция Лейбензона

а

Раскладывая ех в ряд и ограничиваясь тремя членами разложения
(ех = 1 + х +  ),
),
получим


Давления в последней формуле абсолютные. Если положить р0 = р ат то можно записать формулу для Qm через избыточные давления рк и рс

Разность между объемным дебитом с учетом сжимаемости и дебитом, определяемым по формуле Дюпюи, равна:

что составляет от дебита, определяемого по формуле Дюпюи

величину

Следовательно, при установившемся режиме фильтрации дебит можно определить по формулам для несжимаемой жидкости.






