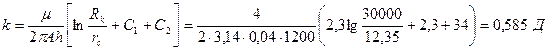Скважина называется гидродинамически совершенной, если она вскрывает пласт на всю мощность и забои скважины открытый, т. е. вся вскрытая поверхность забоя является фильтрующей поверхностью. Поток жидкости к совершенной скважине — плоский фильтрационный поток.
Если скважина с открытым забоем вскрывает пласт не на всю мощность, а только на некоторую величину b, или если скважина сообщается с пластом через отдельные отверстия, то фильтрация жидкости или газа будет пространственной (трехмерной), а скважина — гидродинамически несовершенной.
Различают три вида несовершенства скважин:
1) скважина гидродинамически несовершенная по степени вскрытия пласта — это скважина с открытым забоем, вскрывшая пласт не на всю мощность;
2) скважина гидродинамически несовершенная по характеру вскрытия пласта — скважина, вскрывающая пласт от кровли до подошвы, но сообщающаяся с пластом через отверстия в колонне труб, в цементном кольце или в специальном фильтре;
3) скважина гидродинамически несовершенная как по степени вскрытия пласта, так и по характеру вскрытия.
Дебит скважины, несовершенной по степени вскрытия, можно определить по формуле М. Маскета, если радиус пласта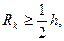 
(V.1)
где
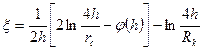(V.2)
и относительное вскрытие пласта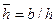 
.
Функция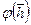 
имеет следующее аналитическое выражение:
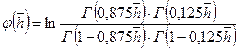(V.3)
где Г — интеграл Эйлера второго рода или иначе, гамма-функция, для которой имеются таблицы в математических справочниках; 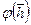представлена графически на рис. 34.
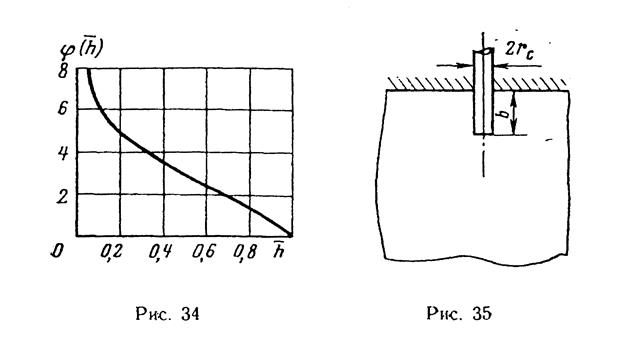
Для скважины в пласте бесконечной мощности (рис. 35) можно найти дебит при помощи формулы Н. К. Гиринского
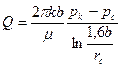(V.4)
Дебит скважины гидродинамически несовершенной как по степени, так и по характеру вскрытия пласта можно подсчитать по формуле
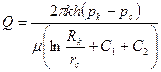(V.5)
где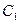 
— безразмерная величина, определяющая дополнительное фильтрационное сопротивление, обусловленное несовершенством скважины по степени вскрытия пласта; С2 — безразмерная величина, определяющая дополнительное фильтрационное сопротивление, вызванное несовершенством скважины по характеру вскрытия пласта.
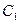и С2 находятся из графиков В. И. Щурова, построенных по данным исследования притока жидкости к скважинам с двойным видом несовершенства на электролитических моделях,
Величина 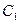представлена на рис. 36 в зависимости от параметров a = h/Dc и .
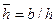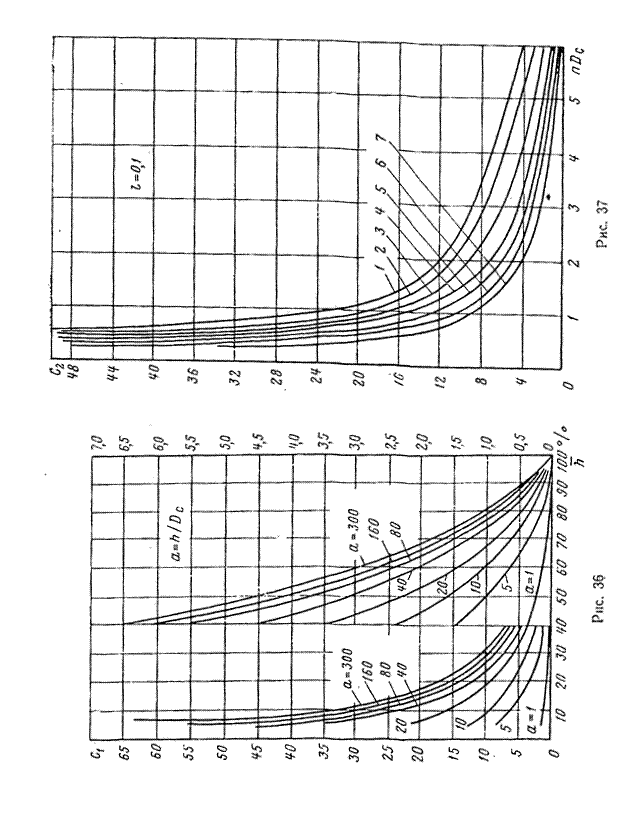
На рис. 37, 38, 39 дана зависимость С2 от трех параметров:
, 
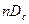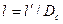и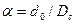 
где п — число перфорационных отверстий на 1 м; Dc — диаметр скважины в м; Г — глубина проникновения пуль в породу; d0 — диаметр отверстий.
Соответствие между кривыми и значениями параметра 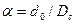видно из следующих данных:
Формулу (V.5) можно записать иначе, введя в нее приведенный радиус скважины
(V.6)
т. е. радиус такой совершенной скважины, дебит которой равен дебиту несовершенной скважины,
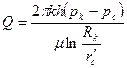(V.7)
Иногда гидродинамическое несовершенство скважин учитывается при помощи коэффициента совершенства скважины
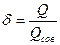(V.8)
где Q — дебит несовершенной скважины;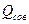 
— дебит совершенной скважины в тех же условиях.
Коэффициент совершенства скважины δ и величина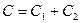 
связаны между собой зависимостью
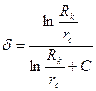(V.9)
или
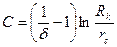(V.10)
В литературе приводятся графики δ, которые можно использовать для оценки С.
3адача 57
Пласт мощностью h = 50 м вскрыт скважиной радиусом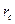 
=12,35 см на малую глубину b = 0,4 м. Расстояние до контура питания 
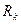=1 км, коэффициент проницаемости пласта k = 0,4 Д, динамический коэффициент вязкости нефти µ = 2мПа•с, давление на контуре питания рк =9,8 МПа (100 кгс/см2),. давление на забое скважины рс = 7,84 МПа (80 кгс/см2).
Найти дебит скважины по приближенному решению Чарного и сопоставить с дебитом, определенным по формуле Маскета.
Указание. На некотором расстоянии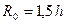 
от оси скважины провести мысленно цилиндрическую поверхность, соосную со скважиной (рис. 40).
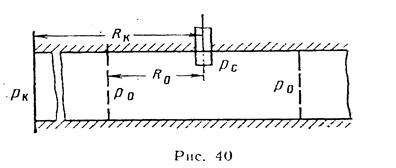
Фильтрационный поток между контуром питания 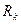и цилиндрической поверхность радиуса 
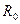считать практически плоскорадиальным с давлением р0 на границе.
Поток между вспомогательной поверхностью радиуса 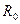и скважиной рассматривать как радиально-сферический к скважине с полусферическим забоем, радиус Rc которого определяется из условия
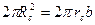
Ответ:
; 
; 
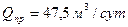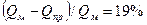
Задача 58
Гидродинамически несовершенная скважина вскрывает пласт мощностью 20 м на глубину 10 м. Радиус скважины 10 см, радиус контура питания 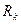= 200 м.
Каково превышение фактического дебита, определенного по формуле Маскета, над дебитом в случае строго плоскорадиального потока к скважине с частичным вскрытием пласта?
Решение. Дебит, определенный по формуле Маскета, равен
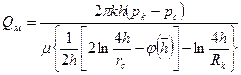
где
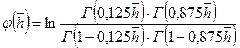
Дебит в случае строго плоскорадиального потока к скважине с частичным вскрытием пласта определяется по формуле Дюпюи в предположении, что мощность пласта равна вскрытию b:
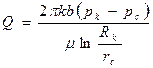
Отношение дебитов
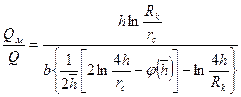
Подсчитаем значение функции 
, для чего найдем значения гамма-функции по таблицам, используя свойство гамма-функции
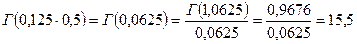
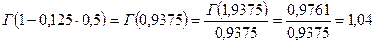
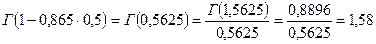
Отсюда
Отношение
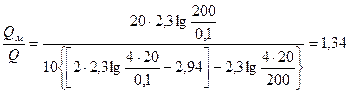
Дебит, определенный по формуле Маскета, оказывается на 34% больше, чем дебит, определенный без учета притока к скважине из нижней части пласта мощностью h — b.
Задача 59
Используя решения Маскета и графики В. И. Щурова, определить коэффициент С1, учитывающий несовершенство скважины по степени вскрытия. Известно, что скважина диаметром dc = 203 мм вскрывает пласт мощностью h = 25 м на глубину b = 5 м. Расстояние до контура питания 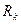=1000 м.
Ответ: по Маскету C1 = 15,1. По Щурову C1 = 15,0.
Задача 60
Используя график В. И. Щурова, найти коэффициенты C1и C2, определяющие дополнительные фильтрационные сопротивления, обусловленные несовершенством скважины, соответственно по степени и по характеру вскрытия, а также приведенный радиус скважины 
, считая, что нефть притекает к скважине диаметром dc = 24,7 см, несовершенной как по степени, так и по характеру вскрытия. Мощность пласта h =12 м, вскрытие пласта b =7м, число прострелов на 1 м вскрытой мощности пласта n = 17 отв./м, глубина проникновения пуль в породу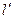 
= 6,25 см, диаметр отверстия do =l.l см.
Ответ: C1 = 2,3; С2 = 2,3; = 0,123 см.
Задача 61
Определить коэффициент совершенства скважины, несовершенной по характеру вскрытия. Забой скважины обсажен и перфорирован при помощи кумулятивного перфоратора, число круглых отверстий на 1 м n=10, диаметр отверстия do =16 мм, длина канала 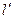=100 мм, радиус скважины 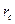=10 см, расстояние до контура питания 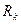= 500 м.
Ответ: δ = 0,825.
Задача 62
Определить коэффициент C1, учитывающий дополнительное фильтрационное сопротивление, приведенный радиус и коэффициент совершенства δ гидродинамически несовершенной по степени вскрытия скважины радиусом 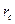= 0,1 м, находящейся в пласте с круговым контуром питания. Мощность пласта h =16 м, мощность вскрытой части пласта b = 9,6 м, радиус контура питания 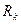=1км.
Ответ: C1 = 2,4; =0,907 см; δ = 0,793.
Задача 63
Какому коэффициенту С, определяющему дополнительное фильтрационное сопротивление, обусловленное гидродинамическим несовершенством скважины, соответствует δ = 0,75? Радиус скважины 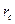= 0,1 м, радиус контура питания 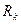=1 км. Определить также приведенный радиус скважины.
Ответ: С =3,067; =0,466 см.
Задача 64
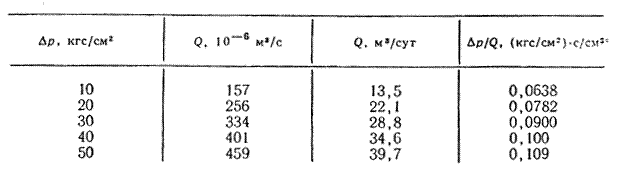Скважину исследовали по методу установившихся отборов, изменяя диаметр штуцера и замеряя забойное давление глубинным регистрирующим манометром. Результаты замеров приведены ниже.
Определить коэффициент проницаемости, если мощность пласта h =12 м, вскрытие пласта b = 7 м, диаметр скважины dc = 24,7см, число прострелов на один метр вскрытой мощности пласта n = 8, глубина проникновения пуль в породу 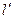= 0 диаметр пулевого канала d =l,l см, половина расстояния до соседних скважин σ = 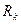= 300 м, динамический коэффициент вязкости жидкости µ = 4 сП.
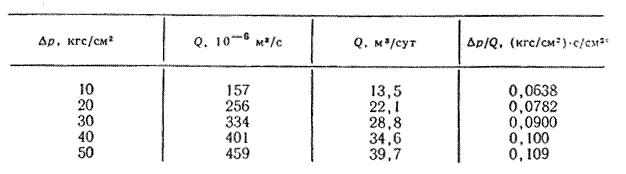
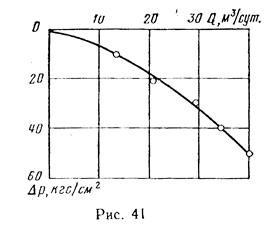
Решение. Из данных исследования видно, что зависимость между Q и Δр нелинейная, т. е. индикаторная линия не будет прямой (рис. 41). Используя двучленную формулу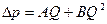 
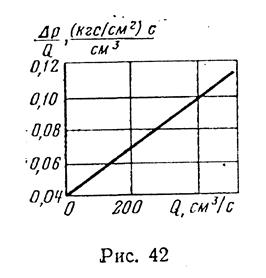
и приведенные данные, построим график зависимости 
от Q (рис 42). Из графика по точке пересечения прямой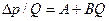 
с осью (осью ординат) найдем значение А = 0 04 (кгс/см2) с/см3, а по тангенсу угла наклона прямой к оси абсцисс (Q)— В =0,00015 (кгс/см2) с2/см6.
Коэффициент проницаемости найдем по полученному значению А из формулы
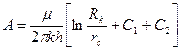
Значения С1 и С2 найдем с помощью графиков Щурова. Определим параметры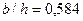 
, 
, 
, 
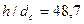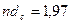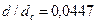и по их значениям —С1 = 2,3 и С2 = 34; при этом найдем коэффициент проницаемости.
