IV. Установившаяся плоская фильтрация

ЖИДКОСТИ. ИНТЕРФЕРЕНЦИЯ СКВАЖИН.

СВЯЗЬ ПЛОСКОЙ ЗАДАЧИ ТЕОРИИ

ФИЛЬТРАЦИИ С ТЕОРИЕЙ ФУНКЦИЙ

КОМПЛЕКСНОГО ПЕРЕМЕННОГО

 

В самом общем случае давление и скорость фильтрации за­висят от трех координат точки в пласте. Если давление и ско­рость фильтрации зависят только от двух координат, то в каждой плоскости, перпендикулярной к третьей оси, поле ско­ростей и давлений будет одинаковым. В этом случае фильтра­ционный поток называется плоским. Плоский фильтрационный поток имеет место при работе одной или нескольких гидроди­намически совершенных (эксплуатационных и нагнетательных) скважин в однородном горизонтальном пласте постоянной мощ­ности. Именно такие потоки будут рассмотрены в настоящем разделе.

 

Потенциал точечного стока и источника на плоскости.

Принцип суперпозиции

 

Назовем точечным стоком па плоскости точку, поглощаю­щую жидкость. Сток можно рассматривать как гидродинами­чески совершенную эксплуатационную скважину бесконечно малого радиуса в пласте единичной мощности. Точечный источ­ник — это точка, выделяющая жидкость (аналог нагнетатель­ной скважины). Заменяя источники и стоки скважинами ко­нечного диаметра, мы практически не допускаем никакой ошибки, поэтому будем в дальнейшем отождествлять скважины с источниками и стоками.

При работе в бесконечном пласте одной скважины-стока фильтрация будет плоскорадиальной и давление в точке на расстоянии rот центра скважины определяется по формуле

(IV.1)

где q=Q/h — дебит скважины-стока, приходящийся на едини­цу мощности пласта; С — постоянная интегрирования.

Назовем потенциалом скорости фильтрации Ф выражение Ф = kp/μ. Переходя от давления к потенциалу, получим значе­ние потенциала в точке на расстоянии rот центра скважины

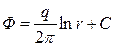(IV.2)

Дебиту источника (нагнетательной скважины) приписыва­ется знак минус.

При совместной работе в пласте нескольких скважин ре­зультирующий потенциал в любой точке пласта М равен ал­гебраической сумме потенциалов Ф₁, Ф₂,..., обусловленных работой каждой отдельной скважины.

(IV.3)

Скорости фильтрации при этом складываются геометрически (рис. 10, а, б). Это называется принципом суперпозиции или сложения течений.

 

Используя принцип суперпозиции, можно приближенно рас­считывать дебиты или забойные потенциалы (а следовательно, и забойные давления) для группы скважин, работающих в пласте с весьма удаленным контуром питания. Потенциал Ф_к на контуре питания считается известным, а расстояние от контура питания до всех скважин — одно и то же и приблизитель­но равно R_к.

Помещая мысленно точку М последовательно на забой каждой скважины, где Ф_м = Ф_сi, получим из общего уравнения (IV.3) систему п уравнений (п — число скважин). Постоянная интегрирования находится из условия на контуре питания. Окончательно система уравнений для определения дебитов или забойных потенциалов примет вид

(IV.4)

…………………………………………………………

здесь r_ij — расстояние между центрами i -той и j -той скважин.

Принцип суперпозиции можно использовать, если скважины работают в пласте, ограниченном контуром питания той или мной формы, или непроницаемыми границами (линии выклинивания, сбросы), но для выполнения тех или иных условий на границах приходится вводить фиктивные скважины за преде­лами пласта, которые создают в совокупности с реальными скважинами необходимые условия на границах.

При этом задача сводится к рассмотрению одновременной работы реальных и фиктивных скважин в неограниченном пласте. Этот метод называется методом отображения источни­ков и стоков. Он широко применяется не только в подземной гидравлике и гидродинамике, но и при решении задач теории электричества, магнетизма и электропроводности.

Так, если эксплуатационная скважи­на находится в пласте с прямолинейным контуром питания на расстоянии а от контура, то ее надо зеркально отобра­зить относительно контура, т. е. поме­стить фиктивную скважину с другой сто­роны от контура на расстоянии а (рис. 11) и считать ее дебит отрицательным (скважина — источник). При этом потенциал в любой точке М равен

на контуре питания r₁ = r₂ и Ф = С=Ф_к, а дебит скважины определяется по формуле

(IV.5)

Метод отображения источников и стоков используется так­же в задачах 52, 53 для нахождения дебита скважины, рабо­тающей в пласте, ограниченном пересекающимися прямолиней­ными непроницаемыми границами. При помощи этого метода можно определить дебит скважины, эксцентрично расположен­ной в круговом пласте

(IV.6)

где δ — расстояние от центра скважины до центра кругового пласта (эксцентриситет).

 

Интерференция скважин

 

Дебит каждой скважины бесконечной цепочки, расположен­ной на расстоянии L от прямолинейного контура питания (рис. 12), выражается формулой

 

 

(IV.7)

где σ - половина расстояния между скважинами. Если L ≥ σ, то приближенно можно принять, что

и тогда

(IV.8)

Дебит одной скважины кольцевой батареи, состоящей из п скважин, в круговом пласте радиуса R_к (рис. 13) имеет вид

где R₁ — радиус батареи; r_с — радиус скважин.

Если число скважин батареи велико (больше пяти или ше­сти), то (R₁/R_к)²ⁿ ≤ 1 и этим выражением можно пренебречь по сравнению с единицей; если, кроме того, заменить

то получим приближенную формулу

(IV. 10)

Формулы (IV.7) и (IV.9) можно вывести, используя метод отображения.

Если в пласте эллипти­ческой формы работает п равноотстоящих друг от друга скважин (рис. 14), то дебит одной скважины определяется по формуле, предло­женной В. Т. Мироненко [11] (IV.11)

 

где β находится из уравнения

(IV. 12).

х — координата центра скважины; L — малая полуось эллипса; σ — половина расстояния между скважинами.