Коэффициенты проницаемости и фильтрации

 

Закон фильтрации Дарси устанавливает линейную зависи­мость между объемным расходом несжимаемой жидкости и по­терей напора, приходящейся на единицу длины, и имеет вид

(I.9)

где и - полные напоры в начальном и конечном сечениях образца пористой среды (скоростные на­поры отброшены вследствие их малости); l — длина образца; ω — площадь поперечного сечения (рис. 3); с — коэффициент фильтрации, зависящий как от свойств пористой среды, так и от свойств фильтрующейся жидкости.

Учитывая, что (H1-H2)/l = i — гидравлический уклон, (1.9) можно записать так:

Q = ciω (I.10)

деля обе части последнего равенства на ω, получим

w = ci. (I.11)

Способность пористой среды пропускать сквозь себя жид­кости и газы называется проницаемостью. Это свойство характеризуется коэффициентом проницаемости k. В отличие от коэффициента фильтрации с коэффициент проницаемости k зависит только от свойств пористой среды.

При решении задач нефтя­ной подземной гидравлики удобнее записывать закон Дарси, пользуясь коэффици­ентом проницаемости:

(I.12)

или

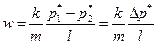
где p₁* = ρgz₁ + p₁ p₂* = ρgz₂ + p₂ — давления, приведенные к плоскости отсчета геометрических высот.

Закон Дарси в дифференциальной форме имеет вид

(I.13)

 

где s — координата вдоль линии тока.

Коэффициенты проницаемости и фильтрации связаны соот­ношением

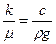(1.14)

Коэффициент проницаемости имеет размерность площади, а коэффициент фильтрации — размерность скорости.

На практике проницаемость нефтяных и газовых пластов измеряется единицами, называемыми дарси (Д). За единицу проницаемости 1 Д принимают проницаемость такой пористой среды, при фильтрации через образец которой площадью 1 см², длиной 1 см при перепаде давления в 1 кгс/см² (98 000 Па) расход жидкости вязкостью 1 сП (1 мПа∙с) составляет 1 см³/с. Величина, равная 0,001 Д, называется миллидарси (мД), 1 Д= 1,02∙10^-8 см² = 1,02.10^{-12 м2}.

Проницаемость реальных пластов изменяется от нескольких миллидарси до нескольких дарси.

 

 

Задача 1

 

Определить пористость ячейки фиктивного грунта (по Слихтеру) в случае, когда угол грани ромбоэдра θ =90° (рис. 4)

Ответ: m = 47,6%.

 

Задача 2

 

Показать, что пористость т и просветность п фиктивного грунта не зависят от диаметра частиц, слагающих грунт. Рассмотреть случай, когда угол грани ромбоэдра θ = 90 ° (рис.4).

Решение. Рассмотрим основ­ную ячейку фиктивного грунта по Слихтеру. Пористость этого элемента

 

откуда следует, что пористость m не зависит от диаметра.

Аналогично для просветности

 

 

 

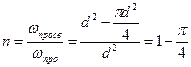
Задача 3

 

Определить удельную поверхность песка (поверхности пес­чинок, заключенных в 1 м³ песчаного пласта), пористость ко­торого m = 25% и эффективный диаметр песчинок d_э =0,2 мм. Найти также число частиц в единице объема пласта, принимая их форму сферической.

Ответ:

 

 

Задача 4

 

Определить пористость фиктивного грунта (по Слихтеру) при наиболее плотной укладке шаровых частиц, соответствующей значению острого угла грани ромбоэдра θ = 60° (рис. 5).

Решение. Объем основной ячейки фиктивного грунта

Значение sin α найдем следующим образом:

из

из

из

 

Подставляя h и ω, полу­чим

Объем скелета ячейки равен объему одной шаро­вой частицы

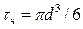
Пористость фиктивного грунта при θ = 60° будет

Задача 5

 

Определить эффективный диаметр песчинок d_э по способу Крюгера — Цункера для песка следующего механического со­става:

 

Диаметр частиц 0 – 0,05 0,05 – 0,1 0,1 – 0,2 0,2 – 0,3 0,3 – 0,5 0,5 – 1,0

мм

Δ g_i,, вес. % 6,9 38,6 44,2 6,3 3,3 0,7

Ответ: d_э = 0,09 мм.

 

 

Задача 6

 

Сопоставить число частиц диаметром d, заключенных в 1 м³ фиктивного грунта, при наиболее свободном расположе­нии частиц (θ = 90°) и при их наиболее тесном расположении (θ = 60°).

Решение. Обозначим число частиц в 1 м³ грунта при θ = 90° через N, а при θ = 60° —через N₁. Тогда

 

 

 

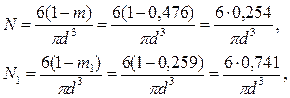
Задача 7

 

Построить кривую механического состава грунта и опреде­лить эффективный диаметр грунта по способу Газена, исполь­зуя следующие данные.

 

Диаметр частиц 0 – 0,05 0,05 – 0,1 0,1 – 0,2 0,2 – 0,3 0,3 – 0,5 0,5 – 1,0

мм

Δg_i,, вес. % 1,5 5,3 7,2 40,1 35,7 10,2

Ответ: d_э = 0,11 мм.

 

Задача 8

 

Определить коэффициент проницаемости пористой среды (в дарси), если известно, что коэффициент фильтрации с = = 0,3∙10^-4 см/с, а кинематический коэффициент вязкости фильтрующейся жидкости v = 10^-6 м²/с. Фильтрация жидкости происходит но закону Дарси.

Ответ: k = 30 мД.

 

Задача 9

 

Определить коэффициент фильтрации, если известно, что площадь поперечного сечения образца песчаника ω = 30 см², длина образца l = 15 см, разность давлений на входе жидкости в образец и на выходе Δ p = 19,6кПа (0,2 кгс/см²), плотность жидкости ρ = 1000 кг/м³ и расход равен 5 л/ч.

Ответ: с = 3,47∙10^-3 см/с.

 

Задача 10

 

Определить скорость фильтрации и среднюю скорость дви­жения нефти у стенки гидродинамически совершенной скважи­ны и на расстоянии r = 75 м, если известно, что мощность пла­ста h = 10 м, коэффициент пористости m = 12%, радиус скважи­ны r_с = 0,1 м, массовый дебит скважины Q_m = 50 т/сут и плот­ность нефти ρ = 850 кг/м³.

Ответ: w_с = 1,09∙10^-4 м/с; υ_с = 0,91∙10^-3 м/с; w = 1,45∙10^-7 м/с; υ = 1,21∙10^-6 м/с.

 

Задача 11

 

Определить объемный дебит Q_c и скорость фильтрации газа w_c у стенки гидродинамически совершенной скважины, если известно, что приведенный к атмосферному давлению и пластовой температуре объемный дебит газа Q_at = 10⁶ м³/сут, радиус скважины r_с = 0,1 м, мощность пласта h = 20 м, абсо­лютное давление газа на забое р_с = 4,9 МПа (50 кгс/см²).

Ответ: Q_c = 0,239 м³/с; w = 0,019 м/с.

 

Задача 12

 

Определить коэффициент пористости, зная, что скорость движения через образец, определяемая при помощи индикато­ра, равна υ = 3∙10^-2 см/с, коэффициент проницаемости k = 0,2 Д, вязкость жидкости μ = 4 мПа∙с и разность давлений Δ р = 2 кгс/см² при длине образца l = 15 см.

Ответ: m = 22%.

 

Задача 13

 

Определить среднее значение скорости фильтрации у входа жидкости в гидродинамически несовершенную по степени вскрытия скважину, если мощность пласта h = 25 м, относи­тельное вскрытие пласта 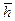= 0,6, радиус скважины r_с = 0,1 м_г дебит жидкости Q = 250 м³/сут.

Ответ: w = 0,0308 см/с.

 

Задача 14

 

Определить коэффициенты проницаемости и фильтрации для цилиндрического образца пористой среды диаметром d = 5 см, длиной l = 20 см, если разность давлений на концах образца составляет 300 мм рт. ст., расход жидкости Q = 1,70 л/ч, динамический коэффициент вязкости жидкости μ = 5 мПа∙с, плотность ее ρ = 0,85 г/см³. Найти также скорость фильтрации.

Ответ: k = 5,9 Д; с= 10^-3см/с; w = 0,024 см/с.

 

Задача 15

 

Определить скорость фильтрации и среднюю скорость дви­жения при плоскорадиалыюй фильтрации газа к скважине в точке на расстоянии r = 150м от центра скважины, если дав­ление в этой точке равно р = 7,84 МПа (80 кгс/см²), мощность пласта h = 12 м, пористость его m = 20%, а приведенный к ат­мосферному давлению и пластовой температуре дебит Q _ат = 2∙10⁶ м³/сут, р _ат = 0,1 МПа.

Ответ: w = 0,262∙10^-4 м/с; υ = l,31∙10^-4 м/с.