Итак, первый тип решающихся с помощью НРА задач – это нахождение определенных условных процентов. Однако, как мы уже заметили, интерпретация результатов регрессионного анализа не сводится к интерпретации отдельных коэффициентов уравнения регрессии. Выше, в начале нашего рассмотрения этого подхода, мы говорили о том, что основная цель его использования в любой науке состоит в получении возможности определенного рода прогноза. Попытаемся проинтерпретировать модели номинального регрессионного анализа с соответствующей точки зрения.
Вернемся к модели общего вида:
Y1 = f1 (Х1, Х2,..., Хn) =
= f1 (
, 
,..., 
, 
, 
,..., 
,..., 
, 
,..., 
)
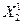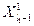Сначала предположим, что мы используем линейные модели.
По тому, какие из коэффициентов уравнения регрессии принимают наибольшие значения, можно судить о тех сочетаниях значений независимых признаков, которые в наибольшей мере детерминируют наличие у респондентов единичного значения зависимого. Другими словами, можно осуществлять поиск взаимодействий. Здесь явно просматривается связь с теми задачами, на решение которых направлены рассмотренные выше алгоритмы типа AID (напомним, более или менее подробно мы рассмотрели алгоритмы THAID и CHAID в п. 2.5.3.2 и 2.5.3.3 соответственно). Это – второй тип задач. Опишем способы их решения более подробно.
Пусть Х1 – как выше, национальность с градациями (русский, грузин, чукча), Х2 – место проживания с градациями (город, село, кочевье), Y – дихотомическая переменная, отвечающая профессии “торговец”. И если при подсчете уравнения линейной номинальной регрессии, к примеру, окажется, что сравнительно большими являются коэффициенты при дихотомических переменных 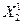(отвечающей свойству “быть грузином”) и (жить в городе), то это будет означать, что именно эти два свойства в совокупности определяют тот или иной уровень доли торговцев в изучаемой группе респондентов. Представляется очевидным сходство этих выводов с теми, которые позволяют получать алгоритмы THAID и CHAID.
Еще более надежными станут выводы подобного рода, если мы будем использовать нелинейные модели. Сразу подчеркнем, что в номинальном регрессионном анализе гораздо легче решается проблема выбора модели, чем в “числовом” варианте этого анализа. Так, здесь резко сокращается круг тех многочленов, среди которых имеет смысл искать интересующие нас закономерности. В частности, ни к чему вставлять в искомое уравнение степени рассматриваемых переменных, поскольку для любого дихотомического признака любая его степень равна самому признаку (так как 02 = 0, 12 = 1). А вот произведения переменных имеет смысл включить. Эти произведения отвечают тем самым взаимодействиям, о которых шла речь выше.
Например, если доля торговцев среди изучаемых респондентов определяется долей горожан-грузин, то мы, несомненно, это выявим путем включения в уравнения произведения вида 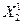´ (обозначения – как выше).
Ясно, что произведения трех дихотомических переменных будут отвечать “трехмерным” взаимодействиям и т.д.
Третий тип задач связан с возможностью осуществлять прогноз несколько иного вида. Поясним это на примере. Вернемся к соотношению (12). В силу его очевидных арифметических свойств, можно сказать, что коэффициенты –0,1 и 0,6 означают вклад, соответственно, свойств “быть русским” (Х1) и “быть грузином” (Х2) в долю торговцев (Y) среди респондентов изучаемой совокупности. Однако проинтерпретировать смысл этого вклада трудно при дихотомических переменных. Поэтому часто прибегают к следующим рассуждениям, опирающимся на довольно сильные модельные предположения. Полагают, что указанное уравнение справедливо не только для того случая, когда Х1 и Х2 – дихотомические переменные, характеризующие отдельных респондентов, но для такой ситуации, когда в качестве единиц наблюдения фигурируют группы людей, а Х1 и Х2 – доли, соответственно, русских и грузин в этих группах. В таком случае смысл уравнения становится ясным: если доля русских увеличивается в группе, скажем, на 10%, то доля торговцев увеличивается на (–0,1)´10% =–1% (т.е. уменьшается на 1%). Если же доля грузин в совокупности увеличивается на 10%, то доля торговцев увеличивается на (0,6)´10 % = 6%.
Заметим, что класс решаемых с помощью техники номинального регрессионного анализа задач может быть расширен за счет использования приемов, широко применяющихся во всем мире при анализе статистического материала, но не рассмотренных в настоящем учебнике. Мы имеем в виду т.н. обобщенные линейные модели (generalized linear model, GLM), в частности, логистическую регрессию, использование т.н. логит-моделей. Коротко опишем суть подхода, уделив особое внимание тому случаю, когда Y – дихотомическая номинальная переменная. То, о чем пойдет речь, можно найти в работах [Agresti, 1996. Ch.4; Demaris, 1992. Ch.4; Menard, 1995].
Напомним, что линейное регрессионное уравнение чаще всего имеет следующий вид:
m = a + b1X1 + b2X2+ … + bkXk.
Левая часть этого уравнения обычно связывается со случайной компонентой рассматриваемой линейной модели. Эта компонента говорит о том, что объясняемая переменная Y является случайной величиной с математическим ожиданием m. О правой части говорят как о систематической компоненте линейной модели. При этом понятие линейности зачастую расширяется: допускается, что одни xi могут выражаться через другие. Например, наличие переменной вида x3 = x1 x2 говорит о взаимодействии между x1 и x2 в процессе их воздействия на Y. Наличие переменной вида x3 = 
свидетельствует о криволинейности воздействия x1 на Y.
Очень важным элементом рассматриваемой модели является форма связи между случайной и систематической компонентами модели. Выше мы говорили о сложности выбора этой формы. Но при этом полагали, что разные виды зависимости можно отразить с помощью преобразования правой части модели. Однако имеет смысл преобразовывать и левую часть. Так, в литературе по анализу данных принято называть связующей функцией (link function) такую функцию g, для которой справедливо соотношение
g(m) = a + b1x1 + b2x2+ … + bkxk.
Если g – тождественная функция (g(m) = m, identity link), то только что написанное соотношение превращается в обычную регрессию. Если же g – это логарифм (log link), то получаем то, что называется логлинейной моделью:
log(m) = a + b1x1 + b2x2+ … + bkxk.
Преимущество использования логлинейной модели заключается в том, что она дает возможность свести изучение сложных взаимодействий между независимыми переменными (т.е. подбор таких произведений х-ов, которые делают адекватной реальности используемую модель; выше мы говорили о важности и трудности решения этой задачи) к поиску коэффициентов линейной зависимости (поскольку логарифм произведения равен сумме логарифмов).
Особую важность имеет т.н. логит-связь (logit link), когда функция g является функцией вида:
Обобщенная линейная модель при использовании такой связи называется логит-моделью (logit model). Эта модель играет большую роль в тех случаях, когда Y – дихотомическая переменная. Используя введенные выше обозначения (р – доля единичных значений Y, а q = (1–р) – доля нулевых значений того же признака) можно сказать, что здесь
Другими словами, функция g является логарифмом отношения преобладания. Ниже для простоты будем предполагать, что у нас только один признак X. Уравнение вида
называется логистической регрессионной функцией. Важность ее изучения представляется очевидной (скажем, для приведенного в предыдущих параграфах примера она позволяет выявить причины изменения соотношения читающих и не читающих данную газету).
Не менее очевидной является важность изучения и т.н. линейной вероятностной модели
р(X) = a + bх
(применительно к тому же примеру, здесь речь идет об изменении доли читающих газету). Заметим, что, когда независимых переменных много, подобного рода уравнения совпадают с теми, которые обычно связываются с логлинейным анализом (там в качестве значений независимой переменной выступают частоты многомерной таблицы сопряженности).
Описанные модели являются очень полезными для социолога. Для интерпретации полученных с их помощью результатов можно использовать описанные в п. 2.6.4 приемы. Отличие будет состоять в трактовке того, что стоит в левой части найденного регрессионного уравнения. Эта трактовка определяется тем, что было только что сказано нами. Ясно, что использование упомянутых моделей расширяет круг решаемых с помощью НРА задач.
Приложения к части II
Приложение I
