≥льк≥сть об'Їкт≥в Ч 357. ƒл€ 348 об'Їкт≥в (що становить 97,48% в≥д загальноњ сукупност≥) в≥доме значенн€ ознаки Ђзадоволен≥сть умовами прац≥ї. ƒл€ ≥нших об'Їкт≥в сукупност≥ (в даному раз≥ њх 9) значенн€ ц≥Їњ ознаки нев≥доме (наприклад, ≥нформац≥€ з≥брана методом опитуванн€, ≥ де€к≥ прац≥вники п≥дприЇмства не захот≥ли в≥дпов≥дати на поставлене питанн€). јнал≥з таблиц≥ св≥дчить, що задоволених умовами прац≥ Ч 45 (12,60% в≥д загальноњ сукупност≥ та 12,93% в≥д к≥лькост≥ прац≥вник≥в, €к≥ в≥дпов≥ли на поставлене запитанн€). ѕереважна б≥льш≥сть прац≥вник≥в повн≥стю або частково не задоволена умовами прац≥.
¬ одновим≥рн≥й таблиц≥ часто перший або другий стовпчики в≥дсутн≥ (тобто в таблиц≥ зазначають або сам≥ значенн€, або њх коди);
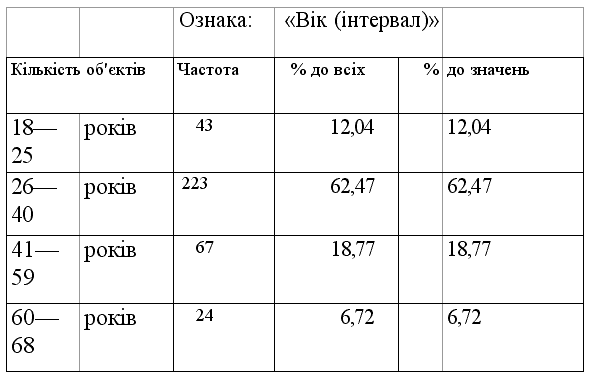
Ќеможливо перел≥чити вс≥ можлив≥ значенн€ ознак, заданих у метричних шкалах. ќтже, неможливо ≥ безпосередньо побудувати одновим≥рну таблицю. «а таких обставин ус≥ можлив≥ значенн€ ознаки розбивають на ≥нтервали, а пот≥м будують таблицю. “ак, дл€ сукупност≥ прац≥вник≥в даного п≥дприЇмства вс≥ значенн€ ознаки Ђв≥кї перебувають м≥ж в≥ком наймолодшого роб≥тника (припустимо, 18 рок≥в) та в≥ком найстаршого роб≥тника (припустимо, 68). –оз≥б'Їмо њх на 4 ≥нтервали: в≥д 18 до 25 рок≥в, в≥д 26 до 40 рок≥в, в≥д 41 до 59 рок≥в та в≥д 60 до 68 рок≥в. “од≥ одновим≥рна таблиц€, що демонструЇ структуру сукупност≥ прац≥вник≥в за в≥ком, матиме такий вигл€д:
“аблиц€ 8
казники вар≥ац≥њ ознак. ƒл€ к≥льк≥сних ознак Ч це дисперс≥€, середнЇ квадратичне в≥дхиленн€, коеф≥ц≥Їнт вар≥ац≥њ. ƒл€ €к≥сних ознак розроблен≥ спец≥альн≥ ≥ндекси €к≥сноњ вар≥ац≥њ. „им б≥льше значенн€ в≥дпов≥дного показника вар≥ац≥њ, тим розс≥€н≥ш≥ навколо середнього значенн€ реальн≥ значенн€ ознаки, а отже, тим з б≥льшою обережн≥стю потр≥бно оперувати ≥з середн≥м значенн€м при побудов≥ зм≥стових висновк≥в.
ћеж≥ вар≥ац≥њ також дають змогу оц≥нити, наск≥льки однор≥дною за певною ознакою Ї сукупн≥сть. якщо сукупн≥сть за певною ознакою неоднор≥дна, може постати потреба под≥лити цю сукупн≥сть на к≥лька однор≥дних за ц≥Їю ознакою частин та анал≥зувати кожну з них окремо. ѕрипустимо, що вивчаЇтьс€ задоволен≥сть умовами прац≥ на певному п≥дприЇмств≥. « лог≥чних м≥ркувань або за результат≥в попередн≥х досл≥джень в≥домо, що зароб≥тна плата прац≥вника впливаЇ на його задоволен≥сть умовами прац≥. Ќехай коеф≥ц≥Їнт вар≥ац≥њ зароб≥тноњ плати дл€ вс≥Їњ сукупност≥ прац≥вник≥в дор≥внюЇ 0,7. “од≥ необх≥дно под≥лити всю сукупн≥сть прац≥вник≥в на групи, приблизно однаков≥ за р≥внем зароб≥тноњ платн≥ (щоб у кожн≥й груп≥ коеф≥ц≥Їнт вар≥ац≥њ зарплати був нижчим в≥д 0,4), та анал≥зувати задоволен≥сть умовами прац≥ окремо у кожн≥й з них.
” ц≥й таблиц≥ в≥дсутн≥й стовпчик, в €кому зазначен≥ коди ≥нтервал≥в, а оск≥льки в≥домий в≥к ус≥х прац≥вник≥в (Ї в≥дпов≥дн≥ значенн€ дл€ вс≥х об'Їкт≥в), тому трет≥й ≥ четвертий стовпчики зб≥гаютьс€. ћетрична ознака розбита у дан≥й таблиц≥ на р≥зн≥ за розм≥ром (нер≥вном≥рн≥) ≥нтервали. ј нер≥дко доц≥льно розбивати весь д≥апазон значень на ≥нтервали однаковоњ довжини (р≥вном≥рн≥ ≥нтервали).
ƒл€ полегшенн€ анал≥зу великоњ к≥лькост≥ таблиць та забезпеченн€ можливост≥ пор≥вн€нн€ к≥лькох з них обчислюють узагальнююч≥ характеристики р€д≥в розпод≥лу. Ќайчаст≥ше використовують характеристику ЂсереднЇ значенн€ ознакиї. ƒл€ к≥льк≥сноњ ознаки обчислюють њњ середнЇ арифметичне значенн€ щодо вс≥х об'Їкт≥в сукупност≥. ƒл€ €к≥сних ознак такою узагальнюючою характеристикою р€ду Ї Ђмодаї Ч значенн€, що найчаст≥ше зустр≥чаЇтьс€ в одновим≥р-н≥й таблиц≥.
оеф≥ц≥Їнт зв'€зку м≥ж двома ознаками. орел€ц≥йний ≥ регрес≥йний анал≥з
ќдним з важливих завдань анал≥зу Ї встановленн€ та оц≥нка взаЇмозв'€зк≥в м≥ж окремими ознаками дл€ певноњ сукупност≥ об'Їкт≥в. ÷ю роботу починають з побудови корел€ц≥йних таблиць (таблиць спр€женост≥ двох ознак, двовим≥рними таблиц€ми). ¬они дають змогу впор€дковувати ≥нформац≥ю про розпод≥л сукупност≥ об'Їкт≥в за двома ознаками. “ак≥ таблиц≥ мають пр€мокутну форму. ≥льк≥сть р€дк≥в у них дор≥внюЇ к≥лькост≥ можливих значень одн≥Їњ ознаки, а к≥льк≥сть стовпчик≥в Ч к≥лькост≥ можливих значень другоњ ознаки. ” таблиц≥ 9 у кл≥тинц≥ на перетин≥ другого р€дка ≥ третього стовпчика знаходитьс€ число 42 (в центр≥ кл≥тинки) Ч к≥льк≥сть роб≥тниць (значенн€ ознаки Ђстатьї Ч Ђж≥ночаї), що незадоволен≥ умовами прац≥ (значенн€ ознаки Ђзадоволен≥сть умовами прац≥ї Ч Ђнезадоволенийї).
“аблиц€ 9
ƒвовим≥рна таблиц€ (ознаки Ђ—татьї та Ђ«адоволен≥сть умовами прац≥ї)
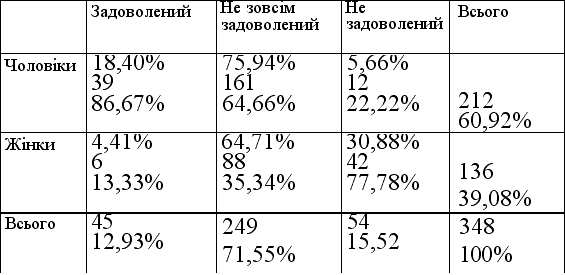
р≥м того, двовим≥рна таблиц€, €к правило, м≥стить ще один додатковий стовпчик ≥ ще один додатковий р€док Ч так зван≥ марг≥нальн≥ стовпчик ≥ р€док. ” таблиц≥ марг≥нали позначен≥ словом Ђ¬сьогої. ожна кл≥тинка марг≥нального стовпчика м≥стить суму чисел в≥дпов≥дного р€дка, тобто к≥льк≥сть об'Їкт≥в, що мають в≥дпов≥дне значенн€ першоњ ознаки (незалежно в≥д того, €кого значенн€ дл€ цих об'Їкт≥в набуваЇ друга ознака), а також в≥дсоток, €кий становить це число щодо загальноњ к≥лькост≥ об'Їкт≥в. “ак, з марг≥нального стовпчика таблиц≥ бачимо, що на п≥дприЇмств≥ працюЇ 136 ж≥нок (39,08% загальноњ к≥лькост≥ працюючих). ћарг≥нальний р€док м≥стить в≥дпов≥дн≥ суми стовпчик≥в таблиц≥.
” кожн≥й кл≥тинц≥ таблиц≥, €к правило, записують в≥дсоток стосовно в≥дпов≥дного значенн€ в марг≥нальному стовпчику (цей в≥дсоток записують вище в≥д самого числа) та в≥дсоток стосовно в≥дпов≥дного значенн€ в марг≥нальному р€дку (записують нижче в≥д числа). якщо знову повернутис€ до кл≥тинки в другому р€дку третього стовпчика таблиц≥, побачимо, що к≥льк≥сть незадоволених умовами прац≥ ж≥нок (таких на п≥дприЇмств≥ 42) становить 30,88 % в≥д загальноњ к≥лькост≥ ж≥нок (всього на п≥дприЇмств≥ 136 ж≥нок) та 77,78% в≥д загальноњ к≥лькост≥ незадоволених умовами прац≥ (всього умовами прац≥ на п≥дприЇмств≥ не задоволен≥ 54 прац≥вники).
„исла в таблиц≥ св≥дчать, що серед ж≥нок в≥дсоток незадоволених умовами прац≥ на п≥дприЇмств≥ значно вищий, н≥ж серед чолов≥к≥в. ќтже, Ї п≥дстави дл€ г≥потези, що стать прац≥вника та його задоволен≥сть умовами прац≥ взаЇмопов'€зан≥.
¬м≥нн€ читати двовим≥рн≥ таблиц≥ приходить з досв≥дом. Ќелегко знаходити законом≥рност≥ в досить великих за розм≥ром таблиц€х. р≥м того, далеко не завжди зв'€зок м≥ж ознаками простежуЇтьс€. “ому на практиц≥ на€вн≥сть зв'€зку м≥ж двома ознаками встановлюють за допомогою так званого критер≥ю %2, €кий базуЇтьс€ на анал≥з≥ частот, записаних у кл≥тинках таблиц≥. ÷е даЇ змогу д≥йти висновк≥в про те, чи можна висувати та анал≥зувати г≥потезу про на€вн≥сть зв'€зку м≥ж двома ознаками.
«астосовуючи зазначений критер≥й, необх≥дно обчислити коеф≥ц≥Їнт х≥-квадрат за формулою (формула залежить в≥д частот у кл≥тинках таблиц≥ та марг≥нальних частот), а одержане значенн€ пор≥вн€ти з табличним (критичним). ѕри цьому сл≥д мати на уваз≥ певний р≥вень значущост≥ (ймов≥рн≥сть прийн€тт€ хибного р≥шенн€) Ч в соц≥олог≥њ, €к правило, 0,05 або 0,01. р≥м того, табличне значенн€ залежить в≥д к≥лькост≥ ступен≥в свободи, що визначають за к≥льк≥стю р€дк≥в ≥ стовпчик≥в таблиц≥. ќтже, дл€ заданого р≥вн€ значущост≥ та к≥лькост≥ ступен≥в свободи необх≥дно знайти в таблиц≥ критичне значенн€ ≥ пор≥вн€ти його з обчисленим. якщо обчислене значенн€ б≥льше в≥д критичного, то факт ≥снуванн€ зв'€зку можна вважати встановленим.
—илу зв'€зку можна оц≥нити обчисленн€м та анал≥зом коеф≥ц≥Їнт≥в спр€женост≥ (ѕ≥рсона, „упрова, рамера). «наченн€ цих коеф≥ц≥Їнт≥в перебувають в ≥нтервал≥ в≥д нул€ до одиниц≥ та мають такий зм≥ст: чим ближче значенн€ до одиниц≥, тим т≥сн≥ший зв'€зок. якщо обидв≥ ознаки, м≥ж €кими вивчають зв'€зок, мають лише по два значенн€ (тобто ф≥ксують на€вн≥сть або в≥дсутн≥сть даноњ ознаки в об'Їкт≥), то дл€ таких Ђчотирикл≥тинковихї таблиць обчислюють коеф≥ц≥Їнти асоц≥ац≥њ та контингенц≥њ.
якщо певному значенню одн≥Їњ величини в≥дпов≥даЇ сукупн≥сть значень другоњ, то м≥ж цими двома величинами ≥снуЇ корел€ц≥йний зв'€зок. ¬≥н ви€вл€Їтьс€ тод≥, коли на досл≥джуване €вище впливаЇ не один, а багато чинник≥в. Ќаприклад, стаж впливаЇ на продуктивн≥сть прац≥, але не остаточно визначаЇ њњ, бо залежить в≥д р≥вн€ осв≥ти, в≥ку, квал≥ф≥кац≥њ прац≥вника та ≥нших фактор≥в. ќск≥льки €вища сусп≥льного житт€ складн≥ та багатофакторн≥, зв'€зок м≥ж ознаками в соц≥олог≥њ практично завжди корел€ц≥йний.
якщо кожному значенню одн≥Їњ ознаки в≥дпов≥даЇ сукупн≥сть значень другоњ ознаки, близько розм≥щених б≥л€ свого середнього значенн€ (тобто вс≥ значенн€ сукупност≥ не дуже в≥др≥зн€ютьс€ в≥д свого середнього арифметичного), то такий корел€ц≥йний зв'€зок вважають сильн≥шим. ≥льк≥сно силу корел€ц≥йного зв'€зку оц≥нюють за допомогою коеф≥ц≥Їнт≥в корел€ц≥њ.
ƒл€ к≥льк≥сних ознак часто використовують коеф≥ц≥Їнт ѕ≥рсона (г), €кий оц≥нюЇ силу зв'€зку за л≥н≥йноњ корел€ц≥њ (тобто в припущенн≥, що значенн€ одн≥Їњ ознаки пов'€зан≥ з в≥дпов≥дними середн≥ми другоњ ознаки л≥н≥йною залежн≥стю). ¬с≥ значенн€ коеф≥ц≥Їнта корел€ц≥њ ѕ≥рсона належать ≥нтервалу в≥д -1 до 1. «нак коеф≥ц≥Їнта показуЇ напр€м зв'€зку: додатне значенн€ св≥дчить про Ђпр€мийї зв'€зок (зростанн€ одн≥Їњ ознаки зумовлюЇ зростанн€ другоњ), в≥д'Їмне значенн€ Ч про Ђзворотнийї зв'€зок, а значенн€ Ђќї Ч про в≥дсутн≥сть л≥н≥йного корел€ц≥йного зв'€зку. Ќаприклад, зв'€зок м≥ж зароб≥тною платою роб≥тника та к≥льк≥стю виготовлених ним деталей Ч пр€мий, а м≥ж зароб≥тною платою та к≥льк≥стю бракованих деталей Ч зворотний. ѕри г =1 або г = -1 маЇмо функц≥ональний зв'€зок м≥ж ознаками (тобто кожному значенню одн≥Їњ ознаки в≥дпов≥даЇ одне значенн€ другоњ ознаки ≥ ц≥ значенн€ пов'€зан≥ л≥н≥йною залежн≥стю). ќтже, чим дал≥ значенн€ коеф≥ц≥Їнта ѕ≥рсона в≥д нул€ (чим б≥льша його абсолютна величина), тим т≥сн≥ший л≥н≥йний корел€ц≥йний зв'€зок ≥снуЇ м≥ж ознаками. јле €кщо г = 0, то це означаЇ в≥дсутн≥сть лише л≥н≥йного зв'€зку, а не в≥дсутн≥сть зв'€зку м≥ж ознаками взагал≥: зв'€зок може ≥снувати, але нел≥н≥йний. ƒл€ оц≥нюванн€ сили нел≥н≥йного зв'€зку використовують корел€ц≥йне в≥дношенн€, що набуваЇ значенн€ м≥ж 0 та 1 (0 означаЇ в≥дсутн≥сть зв'€зку, 1 Ч функц≥ональний зв'€зок).
ƒл€ ознак, заданих у пор€дкових шкалах, обчислюють рангов≥ коеф≥ц≥Їнти корел€ц≥њ (—п≥рмена та ендела), €к≥ також набувають значенн€ м≥ж -1 та 1 та ≥нтерпретуютьс€ так само, €к ≥ коеф≥ц≥Їнт корел€ц≥њ ѕ≥рсона.
¬становленн€ корел€ц≥њ м≥ж двома ознаками ще не означаЇ встановленн€ причинного зв'€зку м≥ж ними. ÷е лише св≥дченн€ того, що одна з ознак частково спричинила ≥ншу або обидв≥ ознаки ≥ Ї насл≥дком де€ких сп≥льних дл€ них причин. «ауважимо, що к≥льк≥сна оц≥нка корел€ц≥йних зв'€зк≥в не може зам≥нити спец≥альних знань, але може допомогти досл≥дников≥ в≥дкинути несуттЇв≥ зв'€зки, ч≥тк≥ше окреслити напр€м пошук≥в, пор≥вн€ти вплив р≥зних чинник≥в тощо. р≥м того, коеф≥ц≥Їнти частковоњ корел€ц≥њ дають змогу оц≥нити зв'€зок м≥ж двома ознаками, усуваючи вплив одн≥Їњ або к≥лькох ≥нших ознак. якщо п≥сл€ усуненн€ впливу третьоњ ознаки коеф≥ц≥Їнт корел€ц≥њ м≥ж двома ознаками зб≥льшуЇтьс€, то трет€ ознака послаблюЇ зв'€зок, а €кщо зменшуЇтьс€, то саме ц€ трет€ ознака певною м≥рою спричин€Ї на€вн≥сть цього зв'€зку (тобто зв'€зок, можливо, Ї лише насл≥дком впливу ц≥Їњ третьоњ ознаки). ќбчислити коеф≥ц≥Їнти частковоњ корел€ц≥њ досить складно через коеф≥ц≥Їнти корел€ц≥њ ѕ≥рсона. ќбс€г обчислень зростаЇ з к≥льк≥стю тих ознак, вплив €ких бажають усунути. —илу сп≥льного зв'€зку сукупност≥ ознак даЇ змогу оц≥нити коеф≥ц≥Їнт множинноњ корел€ц≥њ.
ћетоди регрес≥йного анал≥зу забезпечують не т≥льки оц≥нку сили зв'€зку м≥ж двома ознаками, а й встановленн€ виду цього зв'€зку у вигл€д≥ р≥вн€нн€ (р≥вн€нн€ регрес≥њ), що описуЇ залежн≥сть м≥ж середн≥м значенн€м одн≥Їњ ознаки (залежноњ, повед≥нку €коњ вивчають) та значенн€ми певноњ сукупност≥ ознак (незалежних, вплив €ких на залежну ознаку намагаютьс€ оц≥нити). ” соц≥олог≥чних досл≥дженн€х, €к правило, в≥дбуваЇтьс€ пошук такоњ залежност≥ у л≥н≥йному вигл€д≥ (у вигл€д≥ л≥н≥йного р≥вн€нн€), тому йдетьс€ про р≥вн€нн€ багатовим≥рноњ (множинноњ) л≥н≥йноњ регрес≥њ.
«нанн€ залежност≥ у вигл€д≥ р≥вн€нн€ даЇ змогу не т≥льки по€снювати повед≥нку залежноњ ознаки, а й прогнозувати њњ значенн€ за р≥зних зм≥н значень незалежних ознак. Ќаприклад, на основ≥ анал≥зу фактор≥в, що впливають на р≥вень зароб≥тноњ плати на п≥дприЇмств≥, було побудовано р≥вн€нн€ л≥н≥йноњ регрес≥њ: у = 4,27 xt ■ 1,83 х -9,20. ¬оно описуЇ зв'€зок м≥ж зароб≥тною платою у (залежна ознака, вим≥рюЇтьс€ в гривн€х) ≥ двома незалежними ознаками прац≥вника: стаж Xj (вим≥рюЇтьс€ в роках) та осв≥тн≥й р≥вень х2 (вим≥рюЇтьс€ в роках). јнал≥з цього р≥вн€нн€ наводить на думку, що зростанн€ трудового стажу прац≥вника на один р≥к зумовлюЇ зростанн€ його середньоњ зароб≥тноњ плати на 4,27 грн., а зростанн€ осв≥тнього р≥вн€ на один р≥к Ч зростанн€ середньоњ зароб≥тноњ плати лише на 1,83 грн. ќтже, на даному п≥дприЇмств≥ трудовий стаж суттЇв≥ше впливаЇ на середню зароб≥тну плату прац≥вника, н≥ж його осв≥тн≥й р≥вень. як≥сть р≥вн€нн€ регрес≥њ (наск≥льки точно р≥вн€нн€ регрес≥њ описуЇ зв'€зок м≥ж ознаками) оц≥нюють коеф≥ц≥Їнтом множинноњ корел€ц≥њ.
—уттЇвим дл€ одержанн€ над≥йних, статистично обірунтованих результат≥в Ї оц≥нка значущост≥ статистичних показник≥в. ÷е Ч комплекс математичних процедур, що дають змогу в≥дпов≥сти на низку питань щодо розрахованих статистичних показник≥в ≥ параметр≥в виб≥рковоњ сукупност≥. “ак, обчисливши коеф≥ц≥Їнт корел€ц≥њ м≥ж двома ознаками та одержавши число, що не дор≥внюЇ нулю, ц≥лком лог≥чно постають запитанн€: чи справд≥ цей коеф≥ц≥Їнт суттЇво в≥др≥зн€Їтьс€ в≥д нул€ (а отже, ф≥ксуЇ на€вн≥сть л≥н≥йного корел€ц≥йного зв'€зку), чи ц€ р≥зниц€ випадкова ≥ спричинена лише похибкою нашоњ виб≥рки? ¬≥дпов≥дь на них можна дати, оц≥нивши значущ≥сть в≥дм≥нност≥ коеф≥ц≥Їнта корел€ц≥њ в≥д нул€ ≥ звернувши особливу увагу на обс€г виб≥рки та р≥вень значущост≥ (ймов≥рн≥сть прийн€тт€ хибного р≥шенн€). ÷€ процедура така ж, €к ≥ процедура застосуванн€ критер≥ю х2> ≥ даЇ змогу обчислити за певною формулою критер≥й. ќдержане ж значенн€ пор≥внюЇтьс€ з табличним. Ќа основ≥ результат≥в пор≥вн€нн€ ≥ робитьс€ висновок.
р≥м оц≥нки значущост≥ в≥дм≥нност≥ в≥д нул€ коеф≥ц≥Їнта корел€ц≥њ м≥ж двома ознаками, часто застосовують ≥ процедури оц≥нки значущост≥ р≥зниц≥ м≥ж двома в≥дсотками (наприклад, р≥зниц≥ м≥ж в≥дсотками не-задоволених умовами прац≥ на даному п≥дприЇмств≥ серед ж≥нок ≥ чолов≥к≥в), р≥зниц≥ м≥ж двома середн≥ми (м≥ж середньою зароб≥тною платою на одному та ≥ншому п≥дприЇмствах), двох коеф≥ц≥Їнт≥в корел€ц≥њ. ƒл€ кожноњ такоњ задач≥ ≥снують формула обчисленн€ критер≥ю та статистичн≥ таблиц≥, €кими користуютьс€ дл€ пор≥вн€нн€.
ћетоди багатовим≥рноњ статистики: факторний ≥ кластерний анал≥з
якщо анал≥з даних передбачаЇ використанн€ великоњ к≥лькост≥ взаЇмопов'€заних ознак, доц≥льно застосувати спец≥альн≥ методи та алгоритми багатовим≥рноњ статистики. ÷≥ методи потребують значних обчислень, дл€ ефективного застосуванн€ €ких необх≥дно мати обчислювальну техн≥ку та спец≥альне програмне забезпеченн€. —еред метод≥в багатовим≥рноњ статистики найуживан≥шими Ї факторний та кластерний анал≥з.
—уть факторного анал≥зу пол€гаЇ в тому, що групу сильно скорельованих ознак можна по€снити та описати невеликою к≥льк≥стю прихованих (латентних) фактор≥в, €к≥ безпосередньо не спостер≥гаютьс€, але розкривають значенн€ ознак ц≥Їњ групи. Ќаприклад, за такими ознаками, €к Ђк≥льк≥сть прочитаних книгї, Ђк≥льк≥сть книг у домашн≥й б≥бл≥отец≥ї, Ђк≥льк≥сть в≥дв≥дувань театр≥в ≥ музењвї, приховано фактор, €кий можна було б назвати Ђр≥вень культурного розвитку особистост≥ї. ‘акторний анал≥з даЇ змогу ви€вити ц≥ латентн≥ фактори, описати залежн≥сть м≥ж ними та первинними ознаками, обчислити значенн€ вс≥х побудованих таким чином фактор≥в дл€ кожного об'Їкта. ¬ результат≥ виникаЇ можлив≥сть без значних втрат ≥нформац≥њ перейти в≥д анал≥зу великоњ к≥лькост≥ первинних ознак до анал≥зу пор≥вн€но невеликоњ к≥лькост≥ фактор≥в.
јлгоритми кластерного анал≥зу дають змогу под≥лити сукупн≥сть об'Їкт≥в на однор≥дн≥ за певним формальним критер≥Їм под≥бност≥ групи (кластери). ќсновною властив≥стю цих груп Ї те, що об'Їкти, €к≥ належать одному кластеру, под≥бн≥ш≥ м≥ж собою, н≥ж об'Їкти з р≥зних кластер≥в. “аку класиф≥кац≥ю можна виконувати одночасно за досить великою к≥льк≥стю ознак. Ќаприклад, в≥домо чимало статистичних показник≥в, €к≥ характеризують р≥вень соц≥ально-економ≥чного розвитку адм≥н≥стративних район≥в крањни: к≥льк≥сть населенн€, к≥льк≥сть безроб≥тних, прот€жн≥сть шосейних дор≥г, к≥льк≥сть квадратних метр≥в житла на одну людину тощо. ƒл€ орган≥зац≥њ опитуванн€ необх≥дно згрупувати райони у б≥льш≥ утворенн€ (рег≥они), але варто зробити це так, щоб у кожному такому рег≥он≥ були райони, близьк≥ за своњм соц≥ально-економ≥чним розвитком. ÷е дасть змогу вибрати в такому рег≥он≥ один типовий район ≥ результати опитуванн€ в ньому узагальнити щодо всього рег≥ону. “аке групуванн€ може бути ефективно проведене методом кластерного анал≥зу, оск≥льки у даному раз≥ враховуЇтьс€ та узагальнюЇтьс€ велика к≥льк≥сть показник≥в.
ѕ≥дсумок анал≥зу та ≥нтерпретац≥њ соц≥олог≥чних даних набуваЇ форми документ≥в: зв≥ту за результатами досл≥дженн€, ≥нформац≥йноњ чи анал≥тичноњ дов≥дки. ¬они м≥ст€ть в≥домост≥, висновки та рекомендац≥њ дл€ прийн€тт€ практичних (управл≥нських) р≥шень. ” науково-досл≥дному план≥ Ч це банк соц≥олог≥чних даних наукового анал≥зу.








