“ождества алгебры логики
¬ алгебре логики существует р€д законов и тождественных соотношений, которые примен€ютс€ дл€ преобразовани€ логических выражений. ќни могут быть доказаны путем подстановки в левую и правую части всех наборов аргументов, вход€щих в логическое выражение.
“ождества имеют вид:



 ,
,

 ,
,

 .
.
»з этих тождеств следует:
- если аргумент равен нулю, то его отрицание равно единице и наоборот;
- если хот€ бы один сомножитель равен нулю, то произведение всегда будет равно нулю;
- если хот€ бы одно слагаемое равно единице, то сумма всегда будет равна единице.
«аконы алгебры логики
ѕереместительный закон:
 (2.1)
(2.1)
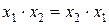 (2.2)
(2.2)
»з этого закона следует, что в выражени€х алгебры логики допустима перестановка мест слагаемых и сомножителей.
—очетательный закон:
 (2.3)
(2.3)
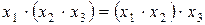 (2.4)
(2.4)
¬ыражени€ (2.3) и (2.4) свидетельствуют о том, что при такой записи функций дизъюнкции и конъюнкции скобки можно опустить.
–аспределительный закон:
 (2.5)
(2.5)
 (2.6)
(2.6)
¬ыражение (2.5) позвол€ет раскрывать скобки и выносить за скобки отдельные аргументы. —праведливость выражени€ (2.6) можно доказать с помощью таблицы истинности.
“аблица 2.1.
| Ќаборы аргументов | Ћева€ часть выражени€ (2.6) | ѕрава€ часть выражени€ (2.6) | |||

| 
| 
| 
| 
| 
|
| 0 0 0 | |||||
| 0 0 1 | |||||
| 0 1 0 | |||||
| 0 1 1 | |||||
| 1 0 0 | |||||
| 1 0 1 | |||||
| 1 1 0 | |||||
| 1 1 1 |
»з таблицы 2.1. следует, что лева€ часть выражени€ (2.6) на всех наборах аргументов равна правой части. “аким образом доказана справедливость данной записи распределительного закона.
«акон инверсии (правило ƒе-ћоргана):
 (2.7)
(2.7)
 (2.8)
(2.8)
ƒл€ доказательства справедливости выражений (2.7) и (2.8) построим таблицы истинности, соответственно таблица 2.2. и таблица 2.3.
“аблица 2.2.
| Ќаборы аргументов | Ћева€ часть | ѕрава€ часть | |||
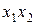
| 
| 
| 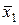
| 
| 
|
| 0 0 | |||||
| 0 1 | |||||
| 1 0 | |||||
| 1 1 |
Ћева€ и права€ части выражени€ (2.7) равны на всех наборах аргументов.
“аблица 2.3.
| Ќаборы аргументов | Ћева€ часть | ѕрава€ часть | |||
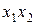
| 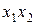
| 
| 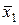
| 
| 
|
| 0 0 | |||||
| 0 1 | |||||
| 1 0 | |||||
| 1 1 |
»з таблицы 2.3. следует, что выражение (2.8) справедливо.
«акон двойного отрицани€:
 .
.
«акон повторени€:
 (2.9)
(2.9)
 (2.10)
(2.10)
¬ыражени€ (2.9) и (2.10) в доказательстве не нуждаютс€.
|
|
|
«акон поглощени€:
 (2.11)
(2.11)
 (2.12)
(2.12)
«акон поглощени€ (2.11) и (2.12) докажем аналитическим путем.
 .
.
 .
.
«акон склеивани€:
 (2.13)
(2.13)
ƒоказательство аналитическое
 . (2.14)
. (2.14)
“еорема разложени€ в р€д функции алгебры
Ћогики
Ћюба€ функци€ алгебры логики может быть разложена в р€д на основании теоремы разложени€. “еорема разложени€ может быть представлена двум€ формами следующим образом:
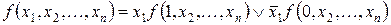 (2.15)
(2.15)
 (2.16)
(2.16)
¬ выражени€х (2.15) и (2.16) функци€ разложена по переменной х 1. “ождества теоремы разложени€ доказываютс€ путем подстановки в левые и правые части тождеств в начале  ,
,  , а затем
, а затем  ,
,  . ¬ обоих случа€х тождества будут одинаковые.
. ¬ обоих случа€х тождества будут одинаковые.
‘ункци€ алгебры логики аналогично может быть разложена по любой из переменных или последовательно по всем переменным.
ѕример 2.1. –азложить функцию  сначала по х 1, а затем по х 2.
сначала по х 1, а затем по х 2.

¬ результате разложени€ заданной функции получили ее стандартную форму.
»з теоремы разложени€ вытекают следующие соотношени€, которые широко используютс€ дл€ упрощени€ функций алгебры логики:
 (2.17)
(2.17)
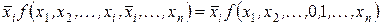 (2.18)
(2.18)
 (2.19)
(2.19)
 (2.20)
(2.20)
ƒокажем справедливость выражени€ (2.17). ƒл€ этого функцию  левой части данного выражени€ разложим по переменной хi и в результате получим
левой части данного выражени€ разложим по переменной хi и в результате получим


 (2.21)
(2.21)
Ћевую и правую части выражени€ (2.21) умножим на хi согласно (2.17) и с учетом тождества  и закона повторени€ получим:
и закона повторени€ получим:


 .
.
јналогично можно доказать соотношени€ (2.18) ¸ (2.20).
—оотношени€ (2.17) ¸ (2.20) позвол€ют сделать следующие выводы:
1. ≈сли в логическом выражении какой-то из аргументов находитс€ в конъюнктивной св€зи с одноименными аргументами или их отрицани€ми, то при упрощении логического выражени€ вместо одноименных аргументов записываетс€ 1, а вместо их отрицани€ 0.
2. ≈сли в логическом выражении отрицание какого-либо аргумента находитс€ в конъюнктивной св€зи с одноименными аргументами или их отрицани€ми, то при упрощении логического выражени€ вместо одноименных аргументов ставитс€ 0, а вместо их отрицаний 1.
3. ≈сли в логическом выражении какой-то из аргументов находитс€ в дизъюнктивной св€зи с одноименными аргументами или их отрицани€ми, то при упрощении логических выражений вместо одноименных аргументов записываетс€ 0, а вместо их отрицаний 1.
4. ≈сли в логическом выражении отрицание какого-либо аргумента находитс€ в дизъюнктивной св€зи с одноименными аргументами или их отрицани€ми, то при упрощении логического выражени€ вместо одноименных аргументов записываетс€ 1, а вместо их отрицаний 0.
ѕример 2.2. ”простить логическое выражение (логическую функцию)  .
.
»спользу€ соотношение (2.17) получим 
 .
.
ѕример 2.3. ”простить логическую функцию 
 .
.
ѕримен€€ соотношение (2.18) получим 
 =
=
 .
.
ѕример 2.4. ”простить логическую функцию 
 .
.
ѕримен€€ соотношение (2.19) получим 
 =
=
 .
.






