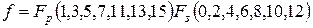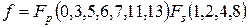јлгебры логики
3.3.1. ћинимизаци€ ‘јЋ с помощью матрицы арно
ћатрица арно представл€ет собой своеобразную таблицу истинности ‘јЋ, котора€ разбита на клетки. оличество клеток матрицы равно 2 n, где n Ц число аргументов ‘јЋ. —толбцы и строки матрицы обозначаютс€ наборами аргументов. ажда€ клетка матрицы соответствует конституэнте единицы ‘јЋ (двоичному числу). ƒвоичное число клетки состоит из набора аргументов строки и столбца. ћатрица арно дл€ ‘јЋ, завис€щей от двух аргументов, представлена в виде таблицы 3.3., от трех аргументов таблицей 3.4. и от четырех аргументов таблицей 3.5.
“аблица 3.3.
| х 2 х 1 | ||
| 0 0 | 0 1 | |
| 1 0 | 1 1 |
“аблица 3.4.
| х 2 х 3 х 1 | ||||
| 0 0 0 | 0 0 1 | 0 1 1 | 0 1 0 | |
| 1 0 0 | 1 0 1 | 1 1 1 | 1 1 0 |
“аблица 3.5.
| х 3 х 4 х 1 х 2 | ||||
| 0 0 0 0 | 0 0 0 1 | 0 0 1 1 | 0 0 1 0 | |
| 0 1 0 0 | 0 1 0 1 | 0 1 1 1 | 0 1 1 0 | |
| 1 1 0 0 | 1 1 0 1 | 1 1 1 1 | 1 1 1 0 | |
| 1 0 0 0 | 1 0 0 1 | 1 0 1 1 | 1 0 1 0 |
летки матриц (таблицы 3.3., 3.4. и 3.5.) пронумерованы дес€тичными эквивалентами двоичных чисел клеток. –€дом расположенные клетки матриц, как по горизонтали, так и по вертикали, содержат соседние двоичные числа. роме этого соседние двоичные числа наход€тс€ во всех столбцах верхней и нижней строк, так же как во всех строках крайних столбцов.
ѕроцесс минимизации ‘јЋ с помощью матрицы арно основан на законе склеивани€ соседних двоичных чисел. ћожно склеивать двоичные числа р€дом расположенных клеток, но рекомендуетс€ склеивать наборы аргументов, которыми обозначены строки и столбцы матриц. –ассмотрим склеивание двоичных чисел клеток первого столбца матрицы (табл. 3.5.).
летки 0 и 4, соответственно двоичные числа 0000 и 0100, результат склеивани€ 0-00.
летки 8 и 12, двоичные числа 1000 и 1100, результат 1-00. ѕолученные импликанты склеиваютс€ между собой, т.к. тире стоит в одном и том же разр€де и двоичные числа импликант €вл€ютс€ соседними, окончательный результат - - 00.
| 0 - 0 0 |
| 1 - 0 0 |
| - - 0 0 |
ќбратим внимание на то, что такой же результат получим, если будем склеивать двоичные числа, которыми обозначены строки матрицы.
летки 0 и 4
| 0 0 |
| 0 1 |
| 0 - |
летки 8 и 12
| 1 1 |
| 1 0 |
| 1 - |
–езультат
| 1 - |
| 0 - |
| - - |
“аким образом, если склеиваютс€ все двоичные числа одного столбца, то пропадают те разр€ды, которыми обозначены строки. јналогично, если будут склеиватьс€ все двоичные числа одной строки, например 4, 5, 7, 6, то пропадают все разр€ды, которыми обозначены столбцы, т.е. результат будет следующий 01- -.
≈сли будут склеиватьс€ двоичные числа только двух любых клеток, то прочерк ставитьс€ вместо того разр€да двоичных чисел строки или столбца, который изменитс€ при переходе клеток из одной строчки в другую (или из одного столбца в другой). Ќапример, склеиваютс€ числа клеток 5 и 13, получим результат -101, или клеток 7 и 6 результат 011-.
|
|
|
ѕри склеивании двоичных чисел восьми р€дом расположенных клеток пропадает три переменные, например дл€ клеток 3, 7, 15, 11, 2, 6, 14, 10 пропадают переменные х 1, х 2, х 3. ѕеременные х 1, х 2 пропадают потому, что склеиваютс€ все клетки столбцов, а х 3 потому, что последние два столбца склеиваютс€ между собой.
ѕрежде, чем рассмотреть примеры минимизации ‘јЋ с помощь матрицы арно, необходимо дать классификацию наборов аргументов, с помощью которых определ€ютс€ функции алгебры логики.
»звестно, что дл€ каждой ‘јЋ имеет место количество наборов аргументов 2 n, где n Ц число аргументов от которых зависит функци€ или логическое выражение.
Ќаборы аргументов дел€тс€ на три вида
1. Ќаборы аргументов, на которых функци€ равна единице, называютс€ рабочими.
2. Ќаборы аргументов, на которых функци€ равна нулю, называютс€ запрещенными.
3. Ќаборы аргументов, на которых функци€ может быть равна или единице, или нулю, называютс€ безразличными.
≈сли заданна€ ‘јЋ не имеет безразличных наборов, то она может быть представлена в буквенном выражении в виде —ƒЌ‘. ѕри наличии в заданной ‘јЋ безразличных наборов, ее представление может иметь следующую форму.
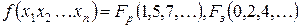 ,
,
где 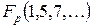 Ц дес€тичные эквиваленты рабочих наборов,
Ц дес€тичные эквиваленты рабочих наборов,
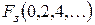 Ц дес€тичные эквиваленты запрещенных наборов.
Ц дес€тичные эквиваленты запрещенных наборов.
Ќаборы аргументов, которых нет среди рабочих и запрещенных, будут безразличными.
ѕример 3.3. ћинимизировать заданную ‘јЋ в виде —ƒЌ‘ с помощью матрицы арно 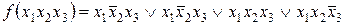 .
.
—ледовательно, функци€ задана только рабочими наборами. ќстальные будут запрещенными. ‘ункци€ зависит только от трех аргументов. —троим матрицу арно и в ее клетках, которые соответствуют рабочим наборам ставим единицы, а в остальных клетках ставим нули.
“аблица 3.5.
| х 2 х 3 х 1 | ||||
 0 0
| ||||
ƒл€ минимизации клетки матрицы, в которых сто€т единицы, объедин€ютс€ в контуры. ¬ контур могут включатьс€ две клетки, четыре или все восемь. ¬ данном примере в контур включены четыре р€дом расположенные клетки одной строки. »мпликантой заданного контура будет 1 - -. –езультат минимизации следующий 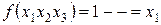 , т.е. произошло сокращение заданной функции в —ƒЌ‘ на 11 букв.
, т.е. произошло сокращение заданной функции в —ƒЌ‘ на 11 букв.
ѕример 3.4. ћинимизировать логическое выражение, заданное рабочими и запрещенными наборами с помощью матрицы арно.
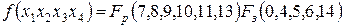
—троим матрицу арно на четыре переменных и заполним клетки единицами и нул€ми соответственно дл€ рабочих и запрещенных наборов.
“аблица 3.6.
| х 3 х 4 х 1 х 2 |
 00 00
| |||
| (1) | ||||
| (1) | (1) | |||
ѕри объединении клеток с единицами в контуры желательно, чтобы в каждый контур включалось наибольшее число клеток из максимально возможного. ƒл€ этого клетки некоторых безразличных наборов используем как клетки рабочих наборов, подставив в них единицы в скобках. ¬ результате получим три контура, содержащие по 4 клетки. ¬ обобщенном коде контура, включающего в себ€ все клетки одной строки, пропадают переменные х 2 х 3 (10 - -). ¬ обобщенном коде контура, включающего все клетки одного столбца пропадают переменные х 1 х 2 (- - 11) и дл€ контура, содержащего по две клетки двух строк пропадают переменные х 2 (при переходе в контуре из одной строки в другую) и х 3 (при переходе из одного столбца в другой). ¬ результате получим минимальную ƒЌ‘ в следующем виде
|
|
|
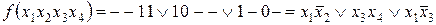 .
.
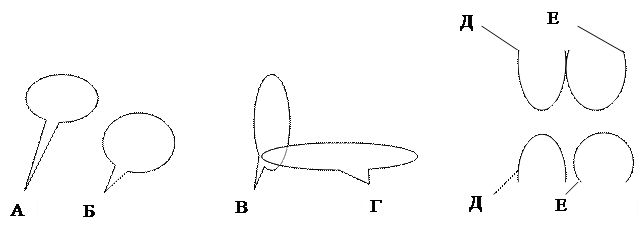
¬озможные варианты объединени€ клеток матрицы арно в контуры показаны на рисунке 3.4.
 х 3 х 4
х 1 х 2 х 3 х 4
х 1 х 2
| ||||||||||||||||


| ј = 0 - 0 - | « = - 0 - 0 | |||||||||||||||
| Ќ | Ѕ = 1 - 1 - | = - - - 1 | ||||||||||||||
| ¬ = - - 0 0 | Ћ = - 1 - - | |||||||||||||||
| √ = 1 0 - - | ћ = - - - 0 | |||||||||||||||
| ƒ = - 0 0 1 | Ќ = - 0 - - | |||||||||||||||
| ≈ = - 0 1 - | ||||||||||||||||
| ∆ = - 1 - 1 |
–ис. 3.1. ¬озможные варианты объединени€ клеток матрицы арно в контуры
3.3.2. ћинимизаци€ функций алгебры логики с помощью матрицы на п€ть переменных
ћатрица минимизации на п€ть переменных строитс€ аналогично матрице арно, т.е. в этой матрице р€дом расположенные столбцы и строки должны быть обозначены соседними двоичными числами наборов переменных
¬ матрице на п€ть переменных (таблица 3.7.) строкам соответствуют наборы переменных х 1 х 2 х 3, а столбцам наборы переменных х 4 х 5. аждой клетке матрицы соответствует п€тиразр€дное двоичное число. ¬ клетках матрицы (табл. 3.7.) проставлены дес€тичные эквиваленты соответствующих двоичных чисел.
“аблица 3.7.
| х 4 х 5 х 1 х 2 х 3 | ||||
|
|
|
ћинимизаци€ ‘јЋ с помощью матрицы на п€ть переменных заключаетс€ в объединении клеток с рабочими наборами (включа€ при необходимости и клетки с безразличными наборами) в контуры и получении дл€ этих контуров соответствующих им обобщенных кодов.
ќсобенность здесь заключаетс€ в том, что в столбцах матрицы на п€ть переменных объедин€ть по четыре клетки в контуры можно только или четыре клетки сверху, или четыре клетки внизу, или четыре клетки посередине. Ќапример, дл€ последнего столбца матрицы контуры могут состо€ть из клеток 2, 6, 14, 10, или 26, 30, 22, 18 или 14, 10, 26, 30.
ѕример 3.6. ћинимизировать с помощью матрицы на п€ть переменных следующее логическое выражение
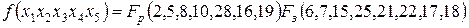
—троим матрицу на п€ть переменных и заполн€ем клетки рабочих наборов единицами, запрещенных Ц нул€ми.
ќбъедин€ем в контуры клетки с рабочими наборами, включа€ в них необходимые клетки безразличных наборов. ƒл€ каждого контура определ€ем обобщенных код.
“аблица 3.8.
х 4 х 5
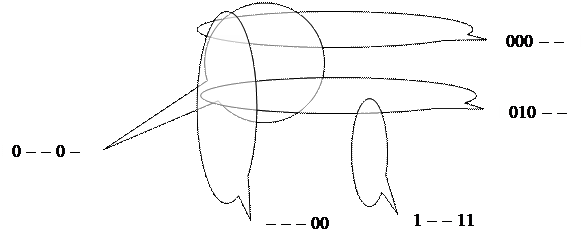 х 1 х 2 х 3 х 1 х 2 х 3
| ||||
| (1) | (1) | (1) | ||
| (1) | ||||
| (1) | (1) | |||
| (1) | (1) | |||
| (1) | (1) | |||
| (1) | ||||
| (1) | (1) | |||
ѕолучаем минимальную ƒЌ‘
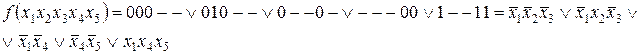
онтрольные вопросы
1. ƒать определение сокращенной ƒЌ‘.
2. „то представл€ет собой тупикова€ ƒЌ‘?
3. ак выбираетс€ минимальна€ ƒЌ‘ из тупиковых ƒЌ‘?
4. ƒл€ чего используетс€ импликантна€ таблица и как она строитс€?
5. ѕо€снить аналитический способ минимизации ‘јЋ вайна-ћак- ласски.
6. ак строитс€ матрица арно на три и четыре переменных?
7. ћинимизировать аналитическим способом следующие логические выражени€, заданные только рабочими наборами

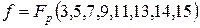
8. ћинимизировать с помощью матрицы арно логические выражени€, заданные рабочими и запрещенными наборами