Функции алгебры логики двух аргументов

И.Д. Долгий

 

 

СИНТЕЗ И АНАЛИЗ

ДИСКРЕТНЫХ УСТРОЙСТВ

 

Ростов-на-Дону

Функции алгебры логики

 

 

Основные понятия и определения

 

В алгебре логики принято сложные высказывания отождествлять с функциями алгебры логики, а простые высказывания с аргументами этих функций. Все высказывания как сложные так и простые могут быть истинными или ложными. Истинные высказывания в числовом выражении равны единице, а ложные нулю.

Таким образом, функцией алгебры логики является такая функция, которая как и ее аргументы, может принимать только два значения 0 или 1.

Все функции алгебры логики определяются на наборах аргументов, число которых равно 2 ⁿ, где n – количество аргументов от которых зависит функция алгебры логики. Под набором аргументов понимается комбинация различных значений аргументов. Если n =1, то количество наборов N будет равно N =2¹=2, т.е. один набор 1 а второй 0. Если n =2, то N =2²=4. Наборы аргументов будут следующие: 00, 01, 10, 11.

На каждом из наборов аргументов функция алгебры логики может принимать значение 0 или 1. Отсюда получается зависимость количества функций М от числа наборов аргументов N

или (от числа аргументов) .

Таким образом, количество функций одного аргумента будет равно , количество функций двух аргументов и т.д.

В настоящее время хорошо изучены и широко используются в теории дискретных устройств только функции одного и двух аргументов.

Функции алгебры логики (ФАЛ) одного

Аргумента

 

Известно, что количество ФАЛ одного аргумента равно четырем. Эти функции представляются следующей таблицей 1.1.

Таблица 1.1.

Нумерация ФАЛ	Наборы аргумента х	Обозначение ФАЛ	Название ФАЛ
f 0				Константа 0
f 1			x	Аргумент х
f 2				Отрицание аргумента х
f 3				Константа 1

 

Из таблицы 1.1. следует, что две функции алгебры логики не зависят от значения аргумента. Функция константа 0 всегда равна 0, а функция константа 1 всегда равна единице при любом значении аргумента х. Функция аргумент х повторяет значение аргумента, функция отрицание аргумента принимает значение противоположное аргументу, т.е. (читается «не икс»).

Все функции алгебры логики могут быть представлены таблицами истинности. Таблица истинности включает в себя все наборы аргументов от которых она зависит и значение функции на каждом наборе. Представим функции одного аргумента таблицами истинности.

Таблица 1.2.

Константа 0

Наборы аргумента

 

 

Таблица 1.4.

Отрицание аргумента

Наборы аргумента

 

Таблица 1.3.

Аргумент х

Наборы аргумента

 

Таблица 1.5.

Константа 1

Наборы аргумента

 

Функции алгебры логики двух аргументов

 

Количество функций двух аргументов равно эти функции представлены в следующей таблице.

Таблица 1.6.

Функции двух аргументов

Аргументы	Наборы аргументов	Аналитическая запись функции	Название функции	Представление ФАЛ двух аргументов в СДНФ
х 1 х 2	0 0 1 1 0 1 0 1
f 0	0 0 0 0		Константа нуля	–
f 1	0 0 0 1		Конъюнкция (логическое произведение)
f 2	0 0 1 0		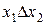Отрицание импликации от х 1 к х 2
f 3	0 0 1 1		Повторение аргумента х 1
f 4	0 1 0 0		Отрицание импликации от х 2 к х 1
f 5	0 1 0 1		Повторение аргумента
f 6	0 1 1 0		Неравнозначность
f 7	0 1 1 1		Дизъюнкция
f 8	1 0 0 0		Отрицание дизъюнкции
f 9	1 0 0 1	~	Равнозначность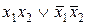
f 10	1 0 1 0		Отрицание аргумента х 2
f 11	1 0 1 1		Импликация от х 2 к х 1
f 12	1 1 0 0		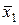Отрицание аргумента х 1
f 13	1 1 0 1		Импликация от х 1 к х 2

 

 

f 14	1 1 1 0		Отрицание конъюнкции
f 15	1 1 1 1		Константа единицы	–

 

Из 16-ти функций двух аргументов необходимо глубоко разобраться и усвоить те функции, на базе которых построены и широко используются логические элементы «И», «ИЛИ», «НЕ», «И-НЕ», «ИЛИ-НЕ».

Логический элемент «И» представляет собой техническую реализацию функции алгебры логики двух аргументов, которая называется конъюнкцией или логическим произведением двух аргументов. Таблица истинности данной функции имеет вид

Таблица 1.7.

ФАЛ конъюнкция

0 0
0 1
1 0
1 1

 

Из таблицы 1.7. следует, что конъюнкция равна единице только в том случае, если оба аргумента х ₁ и х ₂, которые перемножаются, равны единице. Если хотя бы один аргумент равен 0, то логическое произведение будет равно 0. Функцию конъюнкция сокращенно называют функцией «И», потому, что и аргумент х ₁ и аргумент х ₂ должны быть равны единице, чтобы функция была равна единице. В алгебре логики используются следующие знаки умножения: «×», «Ù», «&».

Логический элемент «ИЛИ» построен на основе функции алгебры логики, которая является дизъюнкцией, т.е. логическим сложением аргументов. Значение данной функции представлено в таблице истинности (табл. 1.8.).

Таблица 1.8.

ФАЛ дизъюнкция

0 0
0 1
1 0
1 1

 

Из таблицы 1.8. следует, что ФАЛ дизъюнкция равна единице тогда, когда равен единице или аргумент х₁, или аргумент х₂, или оба аргумента равны единице. Поэтому данную функцию сокращенно называют ФАЛ «ИЛИ».

ФАЛ отрицание конъюнкции («И-НЕ») определяется таблицей истинности (табл. 1.9.).

Таблица 1.9.

ФАЛ «И-НЕ»

0 0
0 1
1 0
1 1

 

ФАЛ отрицание дизъюнкции («ИЛИ-НЕ») определяется таблицей истинности (табл. 1.10.).

Таблица 1.10.

ФАЛ «ИЛИ-НЕ»

0 0
0 1
1 0
1 1

 

Из таблиц 1.9. и 1.10. видно, что функции «И-НЕ» и «ИЛИ-НЕ» принимают значения соответственно противоположные функциям «И» (табл. 1.7.) и «ИЛИ» (табл. 1.8.).

Логические элементы, которые широко используются в электрических схемах автоматики и телемеханики технически реализуют следующие функции алгебры логики:

- ФАЛ одного аргумента отрицание аргумента («НЕ»),

- ФАЛ двух аргументов «И», «ИЛИ», «И-НЕ», «ИЛИ-НЕ» графическое изображение этих логических элементов показано на рис. 1.1.

 

Рис. 1.1. Логические элементы

 

Контрольные вопросы

 

1. Дать определение функции алгебры логики.

2. Что представляет собой таблица истинности функции алгебры логики?

3. Какие существуют ФАЛ, зависящие только от одного аргумента?

4. На основе каких ФАЛ одного и двух аргументов построены логические элементы и их графическое изображение?

5. Что представляет собой набор аргументов?

6. Представить таблицы истинности следующих ФАЛ:

- Конъюнкции,

- Дизъюнкции,

- Отрицание конъюнкции,

- Отрицание дизъюнкции.

7. Составить таблицы истинности следующих функций алгебры логики:

~

~
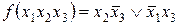