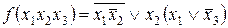стандартным формам функций алгебры логики относ€тс€:
- дизъюнктивна€ нормальна€ форма (ƒЌ‘),
- совершенна€ дизъюнктивна€ нормальна€ форма (—ƒЌ‘),
- конъюнктивна€ нормальна€ форма ( Ќ‘),
- совершенна€ конъюнктивна€ нормальна€ форма (— Ќ‘).
Ќаибольшее применение при синтезе и анализе дискретных устройств наход€т стандартные формы ƒЌ‘ и —ƒЌ‘. этим формам предъ€вл€ютс€ следующие требовани€:
1. ‘ормы должны быть такими, чтобы ими можно было представить любую ‘јЋ.
2. јлгоритм представлени€ ‘јЋ в этих формах не должен быть сложным.
3. ѕредставленна€ в любой из указанных форм ‘јЋ при необходимости должна легко поддаватьс€ преобразовани€м с целью упрощени€ (сокращению числа аргументов).
ƒизъюнктивна€ нормальна€ форма представл€ет собой дизъюнкцию элементарных конъюнкций аргументов, например
 .
.
Ёлементарной конъюнкцией называетс€ логическое произведение любого конечного числа различимых между собой аргументов с отрицани€ми или без них. Ёлементарна€ конъюнкци€ может состо€ть из одного аргумента, двух и более в зависимости от числа аргументов от которых зависит функци€.
Ћюба€ функци€ алгебры логики может быть представлена в виде ƒЌ‘ согласно следующего алгоритма:
1. ѕутем преобразований (использу€ таблицу 1.6.) в заданном логическом выражении оставить только операции Ђ»ї, Ђ»Ћ»ї, ЂЌ≈ї.
2. ќпустить знаки отрицани€ непосредственно на аргументы.
3. –аскрыть скобки, если они имеют место.
4. ќтбросить лишние аргументы в конъюнкци€х согласно закону повторени€.
5. ≈сли имеют место одинаковые элементарные конъюнкции, то лишние отбросить.
|
 . ѕредставить заданное логическое выражение в ƒЌ‘.
. ѕредставить заданное логическое выражение в ƒЌ‘.
–ешаетс€ согласно алгоритма
1. Ќеобходимо избавитьс€ от операции равнозначности, использу€ таблицу 1.6.
 .
.
2. ќпускаютс€ знаки отрицани€ непосредственно на аргументы

 .
.
3. –аскрываютс€ скобки
 .
.

Ћишних аргументов в конъюнкци€х и повтор€ющихс€ конъюнкций нет.
—овершенной дизъюнкцией нормальной формой функций алгебры логики называетс€ дизъюнкци€ конституент единицы.
онституентой единицы называетс€ элементарна€ конъюнкци€, содержаща€ все аргументы данной функции, причем сама функци€ на данном наборе аргументов принимает значение 1. Ќапример

в данном случае функци€ зависит от трех аргументов х 1 х 2 х 3.
¬се слагаемые содержат по три аргумента с отрицани€ми или без них. ‘ункцию алгебры логики заданную в виде ƒЌ‘ можно представить в —ƒЌ‘ (кроме теоремы разложени€) двум€ способами аналитическим или табличным.
јналитический способ представлени€ ƒЌ‘ в —ƒЌ‘ заключаетс€ в использовании двух тождеств  и
и  , т.е. сумма аргумента с его отрицанием всегда равна единице, а умножение любой функции алгебры логики на единицу не мен€ет ее значени€. ¬ элементарных конъюнкци€х ƒЌ‘ отсутствуют некоторые аргументы от которых зависит функци€, например
, т.е. сумма аргумента с его отрицанием всегда равна единице, а умножение любой функции алгебры логики на единицу не мен€ет ее значени€. ¬ элементарных конъюнкци€х ƒЌ‘ отсутствуют некоторые аргументы от которых зависит функци€, например

ƒл€ преобразовани€ данной ƒЌ‘ в —ƒЌ‘ необходимо во все элементарные конъюнкции ввести недостающие аргументы путем умножени€ их на тождества  , где i Ц недостающий аргумент.
, где i Ц недостающий аргумент.
|
|
|
ѕример 2.7. ѕреобразовать ƒЌ‘  в —ƒЌ‘.
в —ƒЌ‘.

ќтсюда следует, что дл€ преобразовани€ ƒЌ‘ в —ƒЌ‘ необходимо:
1. ¬се элементарные конъюнкции ƒЌ‘ умножить на тождества  с недостающими аргументами.
с недостающими аргументами.
2. –аскрыть скобки.
3. ќтбросить лишние слагаемые (конституэнты единицы).
“абличный способ представлени€ ƒЌ‘ в —ƒЌ‘ предусматривает использование таблицы истинности заданной функции, в которую добавл€етс€ столбец с констуентами единицы.
ѕример 2.8. ѕредставить функцию алгебры логики в —ƒЌ‘ табличным способом  (функци€ та же, что и в примере 2.7).
(функци€ та же, что и в примере 2.7).
“аблица 2.4.
“аблица истинности заданной функции
| Ќаборы аргументов | 
| 
| 
| х 1 х 2 | 
| онституэнты единицы |
| х 1 х 2 х 3 | 
| |||||
| 0 0 0 | 
| |||||
| 0 0 1 | 
| |||||
| 0 1 0 | 
| |||||
| 0 1 1 | 
| |||||
| 1 0 0 | 
| |||||
| 1 0 1 | 
| |||||
| 1 1 0 | 
| |||||
| 1 1 1 | 
|
»з таблицы 2.4. следует, что кажда€ конституента равна единице только на своем наборе. ƒл€ получени€ —ƒЌ‘ заданной функции необходимо из таблицы 2.4. в качестве слагаемых —ƒЌ‘ записать все конституенты единицы на которых функци€ равна единице. ¬ результате получим следующую —ƒЌ‘ заданной функции
 .
.
ѕолученна€ —ƒЌ‘ совпадает с —ƒЌ‘ примера 5.2.
онтрольные вопросы
1. ѕредставить и по€снить тождества алгебры логики.
2. ѕредставить и по€снить законы алгебры логики.
3. ƒоказать закон склеивани€.
4. ƒоказать соотношени€, вытекающие из теоремы разложени€.
5. „то представл€ет собой функционально-полный набор функций алгебры логики?
6. Ќазвать возможные функционально-полные наборы (базисы) ‘јЋ.
7. ƒать определение ƒЌ‘.
8. „то представл€ет собой элементарна€ конъюнкци€?
9. ƒать определение —ƒЌ‘.
10. „то представл€ет собой конституента единицы?
11. акие существуют способы представлени€ ƒЌ‘ в —ƒЌ‘?
12. –ешить примеры упрощени€ логических выражений использу€ законы и тождества ‘јЋ, а также соотношени€, вытекающие из теоремы разложени€




13. –ешить пример представлени€ заданных ‘јЋ функционильно-полными наборами Ђ»ї, Ђ»Ћ»ї, ЂЌ≈ї; Ђ»-Ќ≈ї; Ђ»Ћ»-Ќ≈ї




14. –ешить примеры представлени€ заданных функций сначала в виде ƒЌ‘, а затем в виде —ƒЌ‘