Сумарні обсяги оброблення пошти Q ∑ складаються з сумарних обсягів сортування Q сорт і сумарних обсягів обмінювання пошти Q обм.
Сумарні обсяги Q сорт при впровадженні єдиної технології сортування пошти з використанням чотирьох уніфікованих рівнів сортування (рівень 0 – несортована пошта; рівень 1 – несортована пошта, з якої вилучена місцева пошта і пошта округу; рівень 2 – пошта, відсортована до окружних вузлів поштового зв’язку; рівень 3 – пошта, відсортована до відділень поштового зв’язку) практично не залежать від кількості регіональних вузлів.
Сумарні обсяги Q обм пропорційні сумарним обсягам перевезень пошти Р ∑, оскільки перевезення пошти за будь-якими маршрутами пов’язане з обмінюванням пошти між вузлами поштового зв’язку і поштовими маршрутами в пунктах відправлення та з обмінюванням пошти між поштовими маршрутами і вузлами поштового зв’язку в пунктах прибуття.
За таких умов обсяги Q обм залежать від кількості окружних і регіональних вузлів, через які проходять поштові потоки, внаслідок чого значення Q обм в мережі з m = 25 мінімальні, в мережі з m = 1 – середні, в мережі з 1< m < 25 – максимальні.
Велике значення для визначення обсягів Q обм має рівень транзитного оброблення пошти в регіональних вузлах.
У табл. 5.2 наведено операції, що виконуються при різних рівнях транзитного оброблення письмової кореспонденції в регіональних вузлах. Прийнято скорочення: К – контейнер, М – мішок, П – постпакет, Л – лист.
Таблиця 5.2. Операції транзитного оброблення письмової кореспонденції
| Рівень транзитного оброблення | Операції транзитного оброблення | ||||
| Надходження | Розкриття | Сортування | Формування | Відправлення | |
| К | - | К | - | К | |
| К | К | М | К | К | |
| К | К, М | П | М, К | К | |
| К | К, М, П | Л | П, М, К | К |
Якщо до операцій транзитного оброблення пошти, наведених у табл. 5.2, додати не наведені в ній операції вивантаження контейнерів з поштового транспорту у місцях надходження; перевірки відповідності контейнерів супровідній документації у місцях надходження; транспортування контейнерів від місць надходження до місць оброблення; складання супровідної документації відправлення контейнерів у місцях оброблення; транспортування контейнерів від місць оброблення до місць відправлення; перевірки відповідності контейнерів супровідній документації у місцях відправлення; завантаження контейнерів у поштовий транспорт у місцях відправлення та деяких інших операцій, стане зрозумілим, чому транзитне оброблення суттєво збільшує як вартість, так і строки пересилання пошти.
5.3. Оптимізація планів сортування пошти
План сортування поштових відправлень – це документ, що регламентує розподіл напрямів сортування поштівок між накопичувачами сортувальної машини.
Задача побудови плану сортування ставиться так.
Сортувальна машина містить n накопичувачів А 1, А 2, …, Аn.
Поштові відправлення, що надходять на сортування, повинні бути розсортовані за m напрямами N 1, N 2, …, Nm, інформацію про які містять поштові індекси.
Задані ймовірності належності поштівок кожному з напрямів p 1, p 2, …, pm, причому p 1 ³ p 2 ³…³ pm, а p 1 + p 2 +…+ pm = 1.
Відомо, що m > n, внаслідок чого поштівки можуть сортуватися по етапах, тобто проходити через сортувальну машину кілька разів.
Поштівка, адресована за напрямом Ni, сортується si раз (s 1 £ s 2 £ …£ sm).
Необхідно мінімізувати середню кількість сортувань однієї поштівки
s =  .
.
Можливі два основні методи організації сортування: метод виділення напрямів і метод групування напрямів.
Згідно з першим методом на кожному з етапів сортування в кожний з
n - 1 накопичувачів спрямовуються поштівки чергових n - 1 напрямів, тобто виділяються n - 1 зазначених напрямів, решта спрямовується в n -й (збірний) накопичувач, з якого на наступному етапі сортування знову виділяються
n - 1 напрямів аж доки всі поштівки не будуть відсортовані за своїми напрямами.
Поштівки за напрямом Ni будуть сортуватися
si = 
разів, де  – значення Х, округлене до найближчого цілого числа.
– значення Х, округлене до найближчого цілого числа.
Виходячи з цього загальне число етапів сортування складе
k = 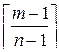
з урахуванням того, що поштівки останнього напряму сортування автоматично залишаються в n -му накопичувачі, а середня кількість сортувань однієї поштівки
S =  .
.
Згідно з другим методом на кожному з етапів сортування поштівки поділяються за напрямами сортування на n груп, кожна з яких спрямовується у відповідний накопичувач, кожна з зазначених груп поштівок на наступному етапі сортування знов поділяється на n груп аж доки в кожному накопичувачі не опиняться поштівки лише одного напряму.
Подаючи число напрямів сортування у виді
nk- 1 < m £ nk,
одержимо середню кількість сортувань однієї поштівки
k - 1 < S £ k,
причому поштівки за напрямами N 1, N 2, …, Nr пройдуть k - 1 етапів сортування, а поштівки за напрямами N r+1, Nr+ 2, …, Nm – k етапів сортування, внаслідок чого середня кількість сортувань однієї поштівки складе
S = (k- 1) 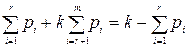 .
.
Значення r може бути одержано з виразу
 ,
,
де [ Х ] – ціла частина Х.
На практиці звичайно використовують комбінований метод сортування, в якому на першому або на першому і наступних етапах сортування частина напрямів виділяється, а решта групується.
На рис. 5.3 наведені приклади сортування поштівок на 100 напрямів за наявності 10 накопичувачів (а – методом виділення напрямів, б – методом групування напрямів, в – комбінованим методом). Цифри в овалах – групи напрямів, цифри в колах – виділені напрями, цифри в прямокутниках – етапи сортування.

Рисунок 5.3. Приклади сортування поштівок
Середня кількість сортувань однієї поштівки складає:
- в схемі рис. 5.3, а
S = (p 1 + p 2 +…+ p 9) + 2(p 10 + p 11 +…+ p 18) + …+ 11(p 91 + p 92 +…+ p 99) + 11 p 100;
- в схемі рис. 5.3, б
S = 2;
- в схемі рис. 5.3, в
S = (p 1 + p 2 + p 3) + 2(p 4 + p 5 +…+ p 70) + 3(p 71 + p 72 +…+ p 100).
Оптимальне співвідношення кількості накопичувачів для напрямів, що виділяються, і для напрямів, що групуються, в схемі комбінованого сортування може бути знайдено з таких міркувань.
Візьмемо за основу схему рис. 5.3, б, в якій S = 2.
Початковий розподіл напрямів сортування за накопичувачами
R 0= í N 1… N 10, N 11… N 20, …, N 91… N 100ý,
за якого в кожний з накопичувачів А 1… А 10 потрапляють поштові відправлення 10 напрямів.
Виділимо напрям N 1, якому відповідає розподіл напрямів сортування
R 1= í N 1, N 2… N 11, N 12… N 21, …, N 82… N 100ý.
З розподілу R 1видно, що в накопичувач А 1 потрапляють поштові відправлення одного напряму, в накопичувачі А 2… А 9 – 10 напрямів, в накопичувач А 10 – 19 напрямів.
З зазначених 19 напрямів на другому етапі сортування виділяються 9 і на третьому етапі 10.
Таким чином, виділення напряму N 1, тобто зменшення на одиницю кількості його сортувань, призводить до збільшення на одиницю кількості сортувань 10 напрямів (N 91… N 100).
Очевидно, що при виконанні нерівності
p 1 > p 91 + p 92 + …+ p 100
виділення напряму N 1 доцільно, а при невиконанні – недоцільно.
Якщо виділення напряму N 1 доцільно, виділимо напрям N 2, якому відповідає розподіл напрямів сортування
R 2= í N 1, N 2, N 3… N 12, N 13… N 22, …, N 73… N 100ý.
Виділення напряму N 2 доцільно, якщо виконується нерівність
p 2 > p 81 + p 82 + … + p 90,
і недоцільно, якщо вона не виконується.
Якщо виділення напряму N 2 доцільно, виділимо напрям N 3, якому відповідає розподіл напрямів сортування
R 3= í N 1, N 2, N 3, N 4… N 13, N 14… N 23, …, N 64… N 100ý.
Виділення напряму N 3 доцільно, якщо виконується нерівність
p 3 > p 71 + p 72 + … + p 80,
і недоцільно, якщо вона не виконується.
Зазначений процес послідовного порівняння ймовірностей напрямів сортування закінчується, якщо чергова нерівність не виконується (в разі виконання всіх нерівностей одержимо схему рис. 5.3, а; в разі виділення напрямів N 1, N 2, N 3 – схему рис. 5.3, в).
Вибір тієї чи іншої схеми сортування визначається заданим розподілом ймовірностей напрямів сортування.






