Нехай маємо деякі двійкові змінні  та
та  :
: 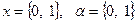 . Введемо позначення
. Введемо позначення  .
.
Тоді змінну  у прямому або інверсному вигляді можна задати як деякий вираз вигляду
у прямому або інверсному вигляді можна задати як деякий вираз вигляду
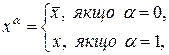
при цьому справедлива рівність
 . (1)
. (1)
Доведемо справедливість формули (1). Дійсно, нехай  тоді згідно з формулою (1) маємо:
тоді згідно з формулою (1) маємо:
 .
.
Аналогічно, якщо  , то
, то
 .
.
Твердження. Вираз  дорівнює одиниці лише тоді, коли
дорівнює одиниці лише тоді, коли 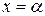 .
.
Справді, нехай  або
або  . Тоді згідно з формулою (1) маємо:
. Тоді згідно з формулою (1) маємо:
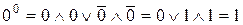 або
або  .
.
Виходячи з наведеного твердження, можна показати, що кон’юнкція вигляду  , де
, де  деякий двійковий набір, дорівнює одиниці, лише при умові, що
деякий двійковий набір, дорівнює одиниці, лише при умові, що 
 .
.
Диз’юнктивне розвинення. Користуючись розглянутими виразами, можна довести наступну теорему.
Теорема. Будь-яку функцію алгебри логіки можна подати у вигляді
 , (2)
, (2)
де  – символ узагальненої диз’юнкції на множині двійкових наборів
– символ узагальненої диз’юнкції на множині двійкових наборів  , кількість яких дорівнює
, кількість яких дорівнює  :
:
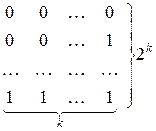
Формула (2) називається диз’юнктивним розвиненням функції алгебри логіки за k змінними.
Наслідок 1. Якщо  , то функцію алгебри логіки можна подати у вигляді
, то функцію алгебри логіки можна подати у вигляді
 . (3)
. (3)
Перевіримо справедливість, одержаної формули безпосередньою перевіркою. Дійсно, при 
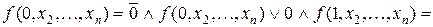

при 
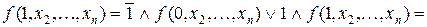

Таким чином, ми одержали, що ліва частина рівності дорівнює правій частині при всіх значеннях змінної  .
.
Наслідок 2. Якщо  , то функцію алгебри логіки можна подати у вигляді
, то функцію алгебри логіки можна подати у вигляді
 (4)
(4)
Наслідок 3. Якщо  , то функцію алгебри логіки можна подати у вигляді
, то функцію алгебри логіки можна подати у вигляді
 . (5)
. (5)
Оскільки в формулі (5) логічне сумування здійснюється за всіма наборами, на яких функція дорівнює одиниці, то вона є не що інше як ДДНФ функції алгебри логіки, яку, як відомо, можна подати у вигляді
 , (6)
, (6)
де  – мінтерми функції
– мінтерми функції  .
.
Кон’юнктивне розвинення. Оскільки формула диз’юнктивного розвинення (2) містить тільки операції  , то застосувавши до неї принцип двоїстості, можемо одержати двоїсте зображення, яке називається кон’юнктивним розвиненням функціїза kзмінними, яке має вигляд:
, то застосувавши до неї принцип двоїстості, можемо одержати двоїсте зображення, яке називається кон’юнктивним розвиненням функціїза kзмінними, яке має вигляд:
 , (7)
, (7)
З формули (7) можна одержати формули кон’юнктивного розвинення, аналогічні до формул диз’юнктивного розвинення для однієї, двох і більше змінних. Зокрема, формули для  ,
,  і
і  мають вигляд:
мають вигляд:
 , (8)
, (8)
 (9)
(9)
 . (10)
. (10)
В формулі (10) логічне множення здійснюється за всіма наборами, на яких функція дорівнює нулю, тобто за всіма макстермами, тому вона є не що інше як ДКНФ, яку можна подати у вигляді
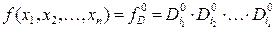 , (11)
, (11)
де  – макстерми функції
– макстерми функції  .
.
Приклад 11. Одержати диз’юнктивне розвинення функції  за: 1) змінною
за: 1) змінною  ; 2) змінними
; 2) змінними  і
і 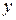 ; 3) всіма змінними.
; 3) всіма змінними.
Розв’язання. За наслідком 1:


2) Для одержання потрібного розкладу скористаємось наслідком 2, для чого обчислимо:
 ;
;  ;
;
 ;
;  .
.
Отже,
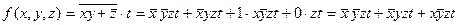
3) Для одержання потрібного розкладу скористаємось наслідком 3, для чого обчислимо:
 ;
;  ;
;
 ;
;  ;
;
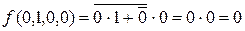 ;
;  ;
;
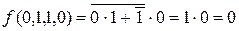 ;
;  ;
;
 ;
; 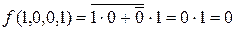 ;
;
 ;
;  ;
;
 ;
;  ;
;
 ;
;  .
.
Таким чином,


Приклад 12. Одержати кон’юнктивне розвинення функції  за: 1) змінною
за: 1) змінною  ; 2) змінними
; 2) змінними  і
і 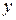 ; 3) всіма змінними.
; 3) всіма змінними.
Розв’язання. 1) Для одержання розкладу за однією змінною  , скористаємось формулою (7)
, скористаємось формулою (7)
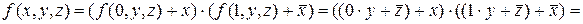
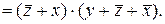
2) Для одержання потрібного розкладу скористаємось формулою (8), для чого обчислимо:
 ;
; 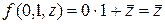 ;
;
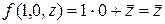 ;
; 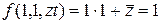 .
.
Отже,
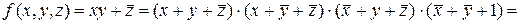
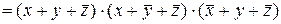 .
.
2) Для одержання потрібного розкладу скористаємось формулою (9), для чого обчислимо:
 ;
;  ;
; 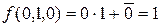 ;
;
 ;
;  ;
;  ;
;
 ;
; 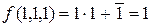 .
.
Отже,  .
.






