Поиск оптимальной последовательности (цепочки) управлений методом динамического программирования

Оптимизация управления n-шагового процесса состоит в том, чтобы найти такую последовательность управлений и₀, и₁ ,..., и_п-1, при которой критерий ка­чества Q(x₀, u) принимает минимальное значение. Это минимальное значение критерия качества управления n-шагового процесса будет зависеть от началь­ного состояния х₀ и его можно обозначать f_n(x₀). По определению имеем:

(5)

Заметим, что первое слагаемое этого выражения Q(x₀,u₀) зависит только от управления u₀, тогда как остальные слагаемые зависят как от u₀,так и от управ­лений на других шагах. Так, Q(x₁,u₁) зависит от u₁, но оно зависит и от и₀ , так как x₁₌ T(x₀, u₀). Аналогично обстоит дело и с остальными слагаемыми. Поэтому вы­ражение (5) можно записать в виде

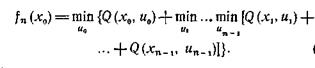
Заметим далее, что выражение

представляет собой минимальное значение критерия ка­чества управления (п-1)- шагового процесса, имеющего начальное состояние . В соответствии с определением эту величину можем обозначить через f_n-1(x₁). Таким образом, получаем:

Эти рассуждения можно повторить, если рассмотреть (п-1)- шаговый процесс, начинающийся с начального состояния . Минимальное значение критерия качества управления для этого случая

Продолжая эти рассуждения, получаем аналогичное выражение для (п-l)-шагового процесса, начинающе­гося с состояния х_l.

Уравнение, называемое часто уравнением Беллмана, представляет собой рекуррентное соотноше­ние, позволяющее последовательно определять опти­мальное управление на каждом шаге управляемого про­цесса и является основой динамического программирования.

Сама идея оптимизации управления на каждом шаге отдельно, если трудно оптимизировать сразу весь про­цесс в целом, не является оригинальной и широко используется на практике. Однако при этом часто не принимают во внимание, что оптимизация каждого ша­га еще не означает оптимизацию всего процесса в целом. Так, жертва фигуры в шахматной партии никогда не бывает выгодна с точки зрения отдельного хода, но она может быть выгодна с точки зрения всей партии. Расход средств на амортизацию может быть невыгоден с точ­ки зрения конъюнктуры на отдельный момент, но он выгоден с точки зрения работы предприятия за длитель­ный период.

Особенностью метода динамического программирова­ния является то, что оно совмещает простоту решения задачи оптимизации управления на отдельном шаге с дальновидностью, заключающейся в учете самых отда­ленных последствий этого шага.

В методе динамического программирования выбор управления на отдельном шаге производится не с точки зрения интересов данного шага, выражающихся в мини­мизации потерь на данном шаге, т. е величины Q(x_l, u_l), а с точки зрения интересов всего процесса в целом, выражающихся в минимизации суммарных потерь Q(x_l, u_l) +f_n-(l+1)(x_l+1) на всех последующих шагах. От­сюда следует основное свойство оптимального процесса, заключающееся в том, что каковы бы ни были началь­ное состояние и начальное управление, последующие управления должны быть оптимальными относительно состояния, являющегося результатом применения пер­вого управления.

Из основного свойства оптимального управления следует, что оптимизация управления для произвольной стадии многошагового процесса заключается в выборе только последующих управлений. Поэтому бывает удоб­но учитывать не те шаги, которые уже были пройдены, а те, которые осталось проделать, для того чтобы при­вести процесс в конечное состояние. С этой точки зре­ния уравнение удобно записать в иной форме.

Величина п-l означает число шагов до конца процесса. Обозначим эту величину через k. При этом величины и будем обозначать просто через х и и. Они будут означать со­стояние объекта и примененное управление за k шагов до конца процесса. Последующее состояние, т. е. то, к которому объект переходит из состояния х при при­менении управления и, обозначим через х'. Это будет x_n-(l+1) в прежних обозначениях. При этом уравнение запишется в виде

(1)

а рекуррентное соотношение примет вид:

(2)

Динамическое программирование является чис­ленным методом решения задачи оптимизации управле­ния.

Определение оптимального управления на произволь­ном k-м шаге, отсчитываемом от момента окончания процесса, находится на основании соотношений (1) и (2), которые для удобства проведения численных расчетов удобно записать в несколько иной форме. Обо­значим через F_k(x, и) величину критерия качества управления k -шагового процесса при оптимальном управ­лении на последних k —1 шагах и произвольном управ­лении на начальном шаге. Тогда соотношение (2) может быть записано в виде

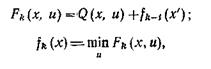
где х' определяется из (1).