Если игра не имеет седловой точки, то возникают затруднения в определении цены игры и оптимальных стратегий игроков. Рассмотрим, например, игру, матрица которой дается табл. 9. В этой игре a=4 и b= 5. Следовательно, первый игрок может гарантировать себе выигрыш, равный 4, а второй может ограничить свой проигрыш величиной 5. Область между b и a является как бы ничейной, и каждый игрок может попытаться улучшить свой результат за счет этой области. Каковы же должны быть в этом случае оптимальные стратегии игроков?
Таблица 9
Если каждый из игроков применяет отмеченную звездочкой стратегию (х2 и yi), то выигрыш первого игрока и проигрыш второго будут равны 5. Это невыгодно второму игроку, так как первый выигрывает больше, чем он может себе гарантировать. Однако если второй игрок каким-либо образом раскроет замысел первого игрока о намерении применить стратегию хa то он может применить стратегию уa и уменьшить выигрыш первого до 4. Правда если первый игрок раскроет замысел второго применить стратегию у2, то, используя стратегию х1 он увеличит свой выигрыш до 6. Таким образом, возникает ситуация, когда каждый игрок должен хранить в секрете ту стратегию, которую он собирается применить. Однако, как это сделать? Ведь если партия играется многократно и второй игрок применяет все время стратегию y2, то первый игрок скоро разгадает замысел второго и, применив стратегию x1,будет иметь добавочный выигрыш. Очевидно, что второй игрок должен менять стратегию в каждой новой партии, но делать это он должен так, чтобы первый не догадался, какую стратегию применит он в каждом случае.
Секретность можно сохранить, если каждый раз выбирать стратегию случайным образом, используя для этого какой-либо механизм случайного выбора. Например, второй игрок может бросить монету и применить стратегию у1 , если выпадет герб, и у2 , если выпадет решетка. Такой способ действия лишает противника всякой возможности узнать наперед о действиях другой стороны.
При использовании механизма случайного выбора выигрыши и проигрыши игроков будут случайными величинами. Результат игры в этом случае можно оценить средней величиной проигрыша второго игрока. Так, если в игре с матрицей вида табл. 13 второй игрок использует стратегии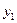 
и у2 случайным образом с вероятностями 0,5, 0,5, то средняя величина его проигрыша при стратегии первого игрока 
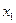будет равна:
а при стратегии первого игрока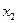 
Следовательно, второй игрок может ограничить свой средний проигрыш величиной 4,5 независимо от стратегии, применяемой первым игроком.
Таким образом, в ряде случаев оказывается целесообразным не намечать заранее стратегию, которая должна быть использована, а выбирать ту или иную стратегию случайным образом, основанным на использовании какого-либо механизма случайного выбора. Стратегию, основанную на случайном выборе, будем называть смешанной стратегией в отличие от рассмотренных ранее заранее намеченных стратегий, которые теперь будем называть чистыми стратегиями.
Пусть G=(X, Y, L) —игра. Пространства X={x1,..., xm} и Y={y1,..., yn}, содержащие перечни всех возможных стратегий игроков, называются пространствами чистых стратегий.
Для получения смешанной стратегии игрок должен использовать некоторый механизм случайного выбора (бросание монеты, бросание игральной кости и т. п.), имеющий число исходов, равное числу чистых стратегий игрока.
Предположим, что механизм случайного выбора первого игрока имеет m исходов, образующих множество R={r(1),..., r(m) }. Обозначим через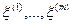 
вероятности, с которыми появляются отдельные исходы механизма случайного выбора.
Смешанная стратегия первого игрока состоит в том, что каждому исходу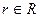 
назначается одна из чистых стратегий 
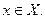При этом величины 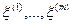будут представлять собой вероятности, с которыми используются чистые стратегии x1,..., xm. Упорядоченное множество 
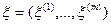, элементы которого удовлетворяют условиям
может теперь рассматриваться как распределение вероятностей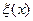 
на пространстве X. Это распределение вероятностей полностью определяет характер игры первого игрока и называется его смешанной стратегией, соответствующей данному механизму случайного выбора.
Другой механизм случайного выбора дает другое распределение вероятностей.
В общем случае первый игрок может располагать бесконечным числом различных механизмов случайного выбора, определяющих всевозможные распределения вероятностей на пространстве своих чистых стратегий:
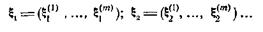
При этом множество
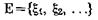
будет представлять собой пространство смешанных стратегий первого игрока.
Аналогично этому второй игрок может использовать свой механизм случайного выбора, определяющий вероятности 
, с которыми будут использоваться чистые стратегии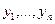 
. При этом упорядоченное множество 
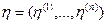, элементы которого удовлетворяют соотношениям
представляет собой распределение вероятностей h(у) на пространстве Y и называется смешанной стратегией второго игрока.
Второй игрок, как и первый, может располагать бесконечным числом различных механизмов случайного выбора, определяющих различные распределения вероятностей на пространстве своих чистых стратегий:
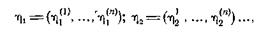
совокупность которых
образует пространство смешанных стратегий второго игрока.
