Одношаговые задачи управления

В одношаговых задачах управление u как таковое не рассматрива­ется, а опре­деляется состоя­ния системы х, обеспечивающие дости­жение поставленной цели.

Одношаговая задача считается за­данной, если известны: пространство состоянии внешней среды с распределением вероятностей для всех 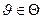, про­странство решений X и критерий качества принятого ре­шения, называемым целе­вой функцией. Целевую функцию, выра­жающую в явном виде цели управления, можно рас­сматривать как выходную величину объекта управления и обозначить через q. Целевая функция является ска­лярной величиной, зависящей от состояния природы J и от состояния объекта управления х, и может быть записана в виде

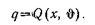
Решение этой задачи со­стоит в нахождении такого , которое обращает в минимум функцию q, т. е. удовлетворяет условию

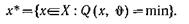
Если стоит задача не минимизации, а максимизации функции q, то необходимо рассматривать функцию .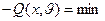

Существует ряд методов решения одношаговой зада­чи принятия решения. Применимость того или иного ме­тода зависит от способа задания множества допустимых решений X, от имеющейся информации о состоянии при­роды и от вида целевой функции q.

Задача называется детерминированной, если нет не­определенности в отношении состояния природы . В де­терминированных задачах пространство состояний при­роды состоит всего из одного элемента , вероятность которого равна единице. В этом случае целевая функция будет зависеть только от состояния объекта управления

Для решения одношаговой задачи широко используются методы математического программирования. Эти методы дают возможность найти значения перемен­ных х₁,...,x_N, удовлетворяющих ограничениям как в виде равенств, так и в виде неравенств и обра­щающих в минимум целевую функцию q(x₁,...,x_N). На переменные обычно накладываются добавочные условия не отрицательности их значений.

Простейшим случаем задачи математического про­граммирования является задача линейного программи­рования. Она соответствует случаю, когда левые части ограничений и целевая функция представ­ляет собой линейные функции от х₁,...,x_N. В задаче линейного программирования требуется найти неотри­цательные значения переменных х₁,...,x_N, которые об­ращают в минимум целевую функцию

и удовлетворяют системе ограничений

где – показатель эффективности приходящийся на единицу переменной х_i, а_ij – затраты ресурса на единицу х_j, m – число ресурсов.

 

Существо задач линейного программирования пояс­ним на ряде примеров.

1. Задача об использовании ресурсов. Для осущест­вления l различных технологических процессов заводу требуется т видов ресурсов S₁,..., S_m (сырье, топливо, материа­лы, инструмент и т. п.). Запасы ресурсов каждого вида ограничены и равны b₁,..., b_m. Известен расход ресурсов на единицу продук­ции по каждому технологическому процессу. Требуется определить, в каком количестве требуется выпускать продукцию каждого вида, чтобы доход от реализации этой продукции был максимальным.

Обозначим через a_ij расход ресурсов вида S_i, на единицу про­дукции вида T_j, а через с_i — доход от реализации единицы про­дукции вида T_j. Все имеющиеся данные представим в виде табл. 1, положив l=3, т=4.

Таблица 1

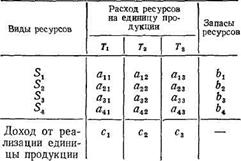
Обозначим через х_j количество единиц выпускаемой продукции вида Т_j. Ограничениями в этой задаче являются требования, чтобы расход ресурсов вида S_i на выпуск всех видов про­дукции не превышал имеющихся запасов:

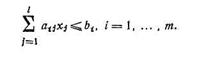
Эти ограничения легко превратить в уравнения, введя перемен­ные 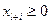, означающие неиспользованные ресурсы вида S_i. При этом получим:

Величина дохода от реализации выпущенной продукции будет равна:

Оптимальным планом выпуска продукции будет такое неотри­цательное решение системы уравнений, при котором целевая функция будет максимальна.

2. Задача о распределении выпуска продукции по предприятиям. План отрасли предусматривает за время Т выпуск следующих видов продукции:

А₁ в количестве N₁ штук;

А₂ в количестве N₂ штук;

A_l в количестве N_l штук.

Эти виды продукции могут выпускаться на r однородных пред­приятиях П₁,…,П_r. Предполагаем, что ни одно предприятие не может одновременно выпускать несколько видов продукции. Кроме того, задано:

— количество продукции А_i, выпускаемой на предприятии П_j, в единицу времени;

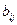— стоимость единицы продукции вида А_i, выпущенной на предприятии П_j;

— время работы предприятия П_j по выпуску продукции А_i.

Требуется найти такие значения , при которых стоимость выпускаемой продукции будет минимальной.

Ограничения:

1) время работы каждого предприятия не должно превышать Т

2) количество выпускаемой продукции должно соответствовать номенклатуре

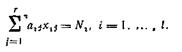
Целевая функция будет представлять собой общую стоимость выпущенной продукции. Если принять во внимание, что величина представляет собой стоимость части продукции А_i, выпу­скаемой предприятием П_j, то общая стоимость выпускаемой продукции

Согласно условиям задачи эта величина должна быть миними­зирована при выполнении ограничений.

3. Транспортная задача. В пунктах P₁,..., P_l имеется однородный груз в количествах , его необходимо перевез­ти в пункты Q₁,..., Q_r в количествах b₁,..., b_r так, чтобы общая стоимость перевозок была минимальна. При этом предполагается, что количество требуемого груза равно имеющимся запасам

Обозначим через x_ij количество груза, перевозимого из пункта Р_i в пункт Q_j, а через с_ij — стоимость перевозки единицы этого груза. В задаче имеются следующие ограничения:

1) количество груза, отправляемого из пункта Р_i на все пунк­ты назначения, должно быть равно имеющимся запасам а_i

2) количество груза, прибываемого в Q_j, со всех пунктов отправ­ления, должно равняться потребности ,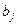

Целевая функция определяет полную стоимость перевозки всех грузов

Рассмотрим примеры составления задач линейного программирования.

Пример 1. Предприятие имеет возможность реализовать не более четырех технологических процессов одновременно, причем тех­нологические процессы П₁ и П₂ используются для производства продукта А, а технологические процессы П₃ и П₄ — для произ­водства продукта В. Расходы, связанные с реализацией каждо­го технологического процесса, определяются трудозатратами (в человеко-неделях), а также количествами (в килограммах) материалов М и N, потребляемых в течение недели. Основ­ные производственно-экономические показатели приведены в табл. 2, где доходы от производства 1 кг продукта выражены в условных денежных единицах и зависят как от вида продукта, так и от используемого технологического процесса.

Таблица 2

Постройте математическую модель задачи о планировании производства с целью получения наибольшего дохода.

Ответ:

где х₁ и х₂ — объемы производства продукта А с использова­нием технологических процессов П₁ и П₂ соответственно; х₃ и x₄ — объемы производства продукта В с использованием тех­нологических процессов П₃ и П₄ соответственно.

Пример 2. Птицеводческая фабрика имеет возможность заку­пать до трех ингредиентов, используемых для приготовления кормовой смеси, расход которой составляет не менее 20 000 кг в неделю. По используемой технологии выращивания цыплят эта смесь должна содержать: а) не менее 0,8 %, но и не более 1,2 % кальция; б) не менее 22 % белка; в) не более 5 % клетчатки.

Постройте математическую модель задачи минимизации недельных затрат на закупки ингредиентов для приготовления кормовой смеси, соответствующей используемому технологи­ческому процессу. Данные, характеризующие стоимость 1 кг каждого ингредиента (в условных денежных единицах) и со­держание в нем (по весу в 1 кг) питательных веществ (кальций, белок, клетчатка), представлены в табл. 3.

 

Таблица 3

Ответ:

где x_k — объем закупок известняка (k = 1), зерна (k=2) и соевых бобов (k=3) в неделю, кг.

Пример 3. Задача по раскрою материала. Листы материала 6х13 м надо раскроить так, чтобы получить заготовки двух видов: 800 штук размером 4х5 м. и 400 штук размером 2х3 м. При этом отходы должны быть минимальными. Способы раскроя материала и количество заготовок каждого типа, полученных при раскрое одного листа, заданы в табл.4.

 

Таблица 4

Размер заготовки	Число заготовок при способах раскроя, шт.
4 х 5 2 х 3

Пусть х_i –число листов, раскроенных i-м способом. Тогда вектор переменных будет иметь вид х=(х₁ , х₂, х₃, х₄).

Объём заготовок (ограничение) можно записать:

Зх₁ + 2х₂ + х₃ = 800,

х₁ + 6х₂ + 9х₃ + 13х₄ = 400.

Отходы материала (целевая функция) определяется по формуле

12х₁ + 2х₂ + 4х₃ = q(x) min.

Линейное программирование

Допустим, дана система т линейно независимых уравнений с n неизвестными x₁,…, х_п, называемая системой ограниче­ний задачи линейного программирования:

Характерной особенностью данной задачи является то, что число уравнений меньше числа неизвестных, т. е. m<n. Требуется найти неотрицательные значения пере­менных 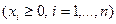, которые удовлетворяют урав­нениям ограничения и обращают в минимум целевую функцию

Иногда в задаче линейного программирования все или некоторые из уравнений имеют вид не­равенств. Так, вместо уравнения

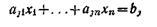
в систему может входить неравенства вида

или

От таких неравенств легко перейти к урав­нениям, вводя добавочную переменную х_n+j³0 так, что­бы в зависимости от знака неравенства имело место одно из двух выражений

Поскольку число переменных п в этой системе больше числа уравнений т, то одно из возможных решений можно найти, если п — т каких-либо переменных положить равными нулю. Полученную при этом систему т уравнений с т неизвестными можно ре­шать обычными методами линейной алгебры. Правда, для того чтобы система т уравнений с т неизвестными имела решение, необходимо, чтобы определитель, составленный из коэффициентов при неизвестных, не обращался в нуль. Если это условие не выполняется, то можно приравнять нулю другие п — т переменных. Полученное при этом решение называется базисным решением.

Базисом называется любой набор т переменных, та­ких, что определитель, составленный из коэффициентов, при этих переменных не равен нулю. Эти т переменных называются базисными переменными (по отношению к данному базису). Остальные п — т переменных называются небазисными или свободными переменными В каж­дой конкретной системе уравнений может сущест­вовать несколько различных базисов с различными ба­зисными переменными.

Если положить все свободные переменные равными нулю и решить полученную систему т уравнений с т неизвестными, то получим базисное решение. Однако среди различных базисных решений будут такие, кото­рые дают отрицательные значения некоторых перемен­ных. Эти базисные решения противоречат условию зада­чи и являются недопустимыми.