Вернемся к задаче распределения ресурсов и зададимся вопросом, какова с точки зрения предприятия ценность имеющихся в его распоряжении ресурсов. При решении этого вопроса будем иметь в виду, что ресурсы, которые предприятие не может полностью использовать, имеют для него очень низкую ценность в том смысле, что предприятие не будет согласно нести даже небольшие расходы на увеличение запасов этих ресурсов. Так, дорогое оборудование, не используемое в технологическом процессе, имеет для предприятия нулевую ценность. Наибольшую ценность будут, очевидно, иметь те ресурсы, которые в наибольшей степени ограничивают выпуск продукции, а, следовательно, и доход предприятия и на увеличение запасов которых предприятие согласно понести значительные расходы на их приобретение.
Поэтому можно считать, что каждый вид ресурса предприятия обладает некоторой «теневой ценой», определяющей ценность данного ресурса для предприятия с точки зрения дохода от реализации выпускаемой продукции и зависящей от наличного запаса этого ресурса и потребности в нем для выпуска продукции.
Если предприятие по каким-либо причинам ограничивается одним технологическим процессом, требующим больших затрат одного из многих имеющихся на предприятии ресурсов, запасы которого ограничены, то теневая цена этого ресурса будет велика. Однако установленные в соответствии с этим технологическим процессом теневые цены на все ресурсы не будут наилучшими, так как введение других технологических процессов позволит более рационально использовать запасы ресурсов. Следовательно, существуют оптимальные теневые цены, которые соответствуют максимальному доходу предприятия, т е. оптимальному распределению ресурсов. Как видим, определение оптимальных теневых цен оказывается тесно связанным с задачей оптимального распределения ресурсов, т. е. с задачей линейного программирования, описываемой системой уравнений и целевой функцией. С математической точки зрения решение двойственной задачи - это поиск области значений ресурсов, в которой достигается глобальный экстремум доходов. Для определения оптимальных теневых цен можно составить самостоятельную задачу линейного программирования.
Обозначим через иi теневую цену единицы ресурса Si. Величины иi должны быть такими, чтобы теневая цена ресурсов, используемых в любом технологическом процессе, не была меньше получаемого дохода, т.е. чтобы расходы не превысили доходов. Запишем это условие в виде:
 , где аij – число единиц i-го ресурса, используемых в j-м продукте.
, где аij – число единиц i-го ресурса, используемых в j-м продукте.
Если ввести переменные ит+j ³0, представляющие собой превышение теневой цены единицы j-й продукции над доходами от ее реализации, то система неравенств превращается в систему уравнений

Оптимальными теневыми ценами будем считать такие, которые минимизируют общую теневую стоимость ресурсов, т. е. величину

Система ограничений совместно с целевой функцией представляет собой новую задачу линейного программирования, получившую название двойственной задачи.
Нетрудно заметить, что прямая и двойственная задача оказываются тесно связанными между собой. Эта связь проявляется в следующем:
- если прямая задача является задачей максимизации целевой функции, то двойственная задача является задачей минимизации;
- коэффициенты целевой функции в прямой задаче являются свободными членами в ограничениях двойственной задачи;
- свободные члены из ограничений прямой задачи становятся коэффициентами целевой функции в двойственной задаче;
- коэффициенты при переменных в ограничениях двойственной задачи представляют собой столбцы таблицы коэффициентов прямой задачи;
- знаки неравенств в ограничениях меняются на противоположные.
Существует тесная связь между решениями прямой и двойственной задач линейного программирования. Для установления этой связи запишем уравнения прямой и двойственной задач в иной форме.
Примем в прямой задаче переменные  свободными и сформулируем ее в следующем виде:
свободными и сформулируем ее в следующем виде:
Максимизировать

при условиях
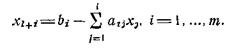 , где xl+i - недоиспользуемый i-й ресурс.
, где xl+i - недоиспользуемый i-й ресурс.
Этой задаче соответствует матрица вида

В двойственной задаче примем за свободные переменные u1,..., ит и сформулируем ее в следующем виде:
Минимизировать

при условиях
 , где Um+j – превышение теневой цены единиц j-й продукции над доходами.
, где Um+j – превышение теневой цены единиц j-й продукции над доходами.
Этой задаче соответствует матрица вида

Как видим, столбцы матрицы являются строками вышерассмотренной матрицы. Следовательно, и прямую и двойственную задачи можем описать одной и той же матрицей, в которой, однако, должно быть установлено следующее соответствие между прямыми и двойственными переменными:

Следует отметить, что любое преобразование матрицы по правилам предыдущего параграфа приведет к новой матрице, которая также будет описывать как прямую, так и двойственную задачи. Следовательно, матрица самого общего вида может служить для описания как прямой, так и двойственной задач линейного программирования. Если при этом элементы первого столбца (за исключением, может быть, а00) положительны, то матрица соответствует допустимому базисному решению прямой задачи. Если положительны элементы первой строки (за исключением, быть может, а00), то матрица соответствует допустимому решению двойственной задачи. Если же в матрице элементы как первого столбца, так и верхней строки (за исключением, быть может, а00) положительные, то матрица соответствует оптимальному решению как прямой, так и двойственной задач. При этом коэффициент а00 дает значение целевой функции, которое при оптимальном решении совпадает как для прямой, так и для двойственной задач:

Пример. Задача на распределение ресурсов задана табл.5. В добавочных графах этой таблицы приведено решение прямой и двойственной задач линейного программирования, т. е. указан оптимальный план распределения ресурсов, остатки ресурсов при оптимальном плане и теневые цены. Из таблицы видно, что ресурсы вида S1, имеющиеся в избытке, имеют нулевую цену. Наивысшую цену имеют ресурсы S2, которые требуются для всех технологических процессов и запасы которых невелики.
Таблица 5
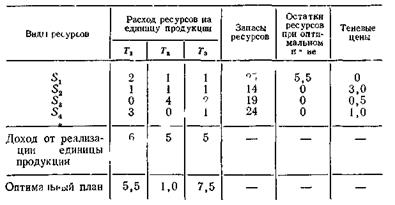
Следовательно, предприятию для повышения доходов необходимо дополнительно приобретать ресурсы S2 , S3, S4.






