Среднее число столкновений в единицу времени и средняя длина свободного пробега молекул

Будем считать газ идеальным, т.е. будем считать, что за исключением момента столкновения молекулы не взаимодействуют между собой и движутся прямолинейно. В момент столкновения направление скорости молекулы изменяется, после чего она снова движется прямолинейно. Путь молекулы в газе представляют собой ломаную линию (рис.3). Расстояние, пройденное молекулой между двумя последовательными столкновениями, называется длиной свободного пробега. Из-за большого числа молекул и их хаотичного движения длины свободного пробега молекулы будут различными.

Поэтому нас будет интересовать средняя длина свободного пробега. Точно также будут различными и число столкновений, испытываемых молекулой в единицу времени и следует говорить только о среднем значении этой величины. Эти две величины - средняя длина свободного пробега и среднее число столкновений в единицу времени - являются основными характеристиками процесса столкновения газовых молекул.

Среднее число столкновений, испытываемых молекулой газа в единицу времени, можно определить из следующих соображений. Молекулы будем считать твердыми шариками радиуса r (рис.4).

Пусть одна из молекул движется по прямой в газе, в котором частицы равномерно распределены по объему, так, что в единице объема находится n молекул.

Вначале предположим, что все молекулы, кроме одной, находятся в покое. Движущаяся молекула пройдет за 1 секунду расстояние 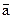, равное ее средней скорости ,

при этом она сталкивается со всеми молекулами, которые окажутся на ее пути. Это будут те молекулы, центры которых расположены в объеме цилиндра длиной и площадью основания, равной эффективному сечению . Объем этого цилиндра 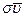, а число молекул в нем . Таким же будет и число столкновений Z, которые испытывает движущаяся молекула. Z= .

Надо отметить, что молекула не может двигаться прямолинейно, поскольку она сталкивается с другими молекулами. Путь, проходимый молекулой, зигзагообразный, как на рис.5. Это, однако, не изменяет результата расчета; пологая, что молекула движется прямолинейно, мы только мысленно выпрямляем ломаный цилиндр. Следует еще учесть, что движутся все молекулы газа. Это значит, в выражение для Z должна входить не абсолютная скорость молекулы, а скорость ее относительно тех молекул, с которыми она сталкивается . Можно показать, что относительные скорости связаны с абсолютной скоростью соотношением = . Тогда для среднего числа столкновений одной молекулы в единицу времени получим формулу:

. (4.1)

Чтобы найти число столкновений, испытываемых всеми молекулами в единицу времени, нужно умножить Z на число молекул N в газе. Но так как в каждом столкновении участвуют две молекулы (одновременное столкновение трех и более молекул маловероятно), то это число нужно еще разделить на 2, чтобы не считать каждое столкновение два раза. Следовательно, полное число столкновений в газе, содержащем N молекул в единицу времени, равно:

.

Число столкновений в единице объема в единицу времени определится выражением:

.

Зная число столкновений, испытываемых одной молекулой в единицу времени, можно вычислить и среднюю длину свободного пробега. За время t молекула пройдет зигзагообразный путь, равный . Изломов на этом пути будет столько, сколько столкновений испытывала молекула на этом пути. Средняя длина свободного пробега, очевидно, равно отношению длины пути, пройденной молекулой, к числу, испытанных ею на этом пути, столкновений:

=

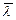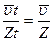
Поставив сюда значение Z из (4.1), получим:

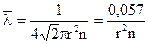. (4.2)

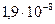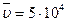Пользуясь формулами (4.1) и (4.2), найдем численные значения для и . Проведем такой расчет, например, для азота при нормальных условиях. Радиус r молекулы азота можно считать равным см, число частиц в единице объема , средняя скорость с м/с. Расчеты показывают , см. Возникает вопрос, можно ли считать идеальным такой газ, в котором частицы каждую секунду сталкиваются миллиарды раз, а между столкновениями свободно проходят очень малые пути, не превосходящие нескольких стотысячных долей сантиметра. Да, можно, поскольку молекулы взаимодействуют друг с другом только в течение того времени, пока они находятся друг от друга на расстоянии порядка их диаметра 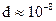см, остальное время движутся свободно. Так как при атмосферном давлении длина свободного пробега молекул 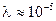см, что примерно в 1000 раз больше размеров молекул, то время пребывания молекулы под взаимным взаимодействием во столько же раз меньше их свободного движения. Другими словами, время столкновения молекул примерно 1000 раз меньше времени между столкновениями, т.е. подавляющую часть времени молекула движется свободно.

Рассмотрим, как зависит длина свободного пробега от термодинамических параметров температуры Т и давления Р. Как видно из формулы (4.2) 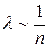. Учитывая, что , можно написать . С уменьшением давления длина свободного пробега возрастает. При определенном значении давления длина свободного пробега может стать равной размерам сосуда, в которой заключен газ, а при дальнейшем падении давления, превзойдет их. Когда длина свободного пробега становится равной или больше размеров сосуда, столкновение молекул в газе практически уже не происходит и весь путь от стенки до стенки молекула проходит двигаясь прямолинейно. Из формулы (4.2) следует, что длина свободного пробега не должна зависеть от температуры, поскольку число частиц в единице объема 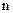с изменением температуры не меняется. Но как показывает опыт, имеется определенная зависимость от температуры. Эта зависимость описывается эмпирической формулой Сюзерленда: 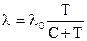, где - значение длины свободного пробега, определяемое по формуле (4.2), С - эмпирическая постоянная. Такая зависимость объясняется тем, что молекулы не являются твердыми шариками, и расстояние между молекулами при столкновении зависит от их кинетической энергии, соответственно и от температуры. Чем выше температура газа, тем больше кинетическая энергия молекул, соответственно молекулы, преодолевая силы отталкивания, могут приблизиться на близкое расстояние, т.е. в формуле (4.1), уменьшается. Это приводит к увеличению длины свободного пробега при повышении температуры.