 . (18)
. (18)
Якщо коефіцієнт  , тоді така асимптота називається горизонтальною
, тоді така асимптота називається горизонтальною  .
.
Пряма 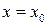 називається вертикальною асимптотою графіка функції
називається вертикальною асимптотою графіка функції  , якщо
, якщо  (або
(або  ).
).
Приклад 2. Знайти асимптоти графіка функції  .
.
За формулою (18) знаходимо коефіцієнти  і
і  нахиленої асимптоти:
нахиленої асимптоти:

Отже, пряма  є нахиленою асимптотою графіка даної функції
є нахиленою асимптотою графіка даної функції  як при
як при 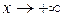 , так і при
, так і при  . Оскільки
. Оскільки  , то горизонтальних асимптот немає.
, то горизонтальних асимптот немає.
Нарешті, точка  є точкою розриву даної функції
є точкою розриву даної функції  , причому
, причому 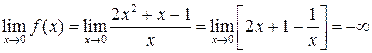 . Отже, пряма
. Отже, пряма  (вісь ординат) є вертикальною асимптотою функції
(вісь ординат) є вертикальною асимптотою функції  , графік якої показано на Рис. 3.4.
, графік якої показано на Рис. 3.4.





 20
20

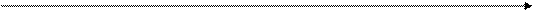

 у
у

 10
10




 0
0












 0 х
0 х
-10


 -20
-20
-2 -1 0 1 2
Рис. 3.4. Графік функції 
Наведемо загальну схему для побудови графіка функції  :
:
1. Знайти область визначення функції.
2. Знайти точки перетину графіка функції з віссю ординат (покласти у формулі, яка задає функцію, х = 0) і віссю абсцис (розв’язати рівняння  )
)
3. Знайти асимптоти функції.
4. Дослідити функцію на екстремум: знайти точки мінімуму, максимуму, а також точки перегину. Обчислити значення функції у цих точках. Встановити ділянки монотонності функції.
5. Побудувати схематичний графік функції  .
.
При побудові графіка важливо врахувати його симетрію. Для цього корисно перевірити функцію на парність (непарність).
Зауваження. Функція  називається парною (непарною), якщо виконується умова:
називається парною (непарною), якщо виконується умова:  .
.
Також важливо перевірити функцію на періодичність:  , де
, де  – період функції
– період функції  .
.
Приклад 3. Побудувати графік функції  .
.
Згідно з наведеною вище схемою:
1. Область визначення функції 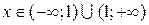 (точка х = 1 є точкою розриву).
(точка х = 1 є точкою розриву).
2. Графік даної функції перетинає вісь ординат у точці  (при
(при  ). Оскільки рівняння
). Оскільки рівняння  не має дійсних коренів, то графік даної функції взагалі не перетинає вісь абсцис.
не має дійсних коренів, то графік даної функції взагалі не перетинає вісь абсцис.
3. Дослідимо поведінку функції поблизу точки розриву х = 1. Маємо:  . Отже, пряма х = 1 є вертикальною асимптотою. За формулами (18) знаходимо:
. Отже, пряма х = 1 є вертикальною асимптотою. За формулами (18) знаходимо:

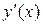 + max – – min +
+ max – – min +
 | |||||||||
 | |||||||||
 | |||||||||
 | |||||||||
 | |||||||||

 1
1 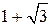 x
x
Рис. 3.5. Дослідження функції на екстремум
Отже, пряма  є нахилена асимптота даної функції. Горизонтальних асимптот немає.
є нахилена асимптота даної функції. Горизонтальних асимптот немає.
4. Знайдемо першу похідну функції і прирівняємо її до нуля:

Відмітивши ці точки на осі х (Рис. 3.5), дослідимо їх на екстремум. Отже,  є точкою максимуму,
є точкою максимуму,  , а
, а 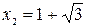 є точкою мінімуму,
є точкою мінімуму,  . Функція зростає на інтервалах
. Функція зростає на інтервалах  і
і  . Функція спадає на інтервалі
. Функція спадає на інтервалі  . З’ясуємо, чи має дана функція точку перегину. Знайдемо її другу похідну:
. З’ясуємо, чи має дана функція точку перегину. Знайдемо її другу похідну:
 . Отже, точок перегину функція немає.
. Отже, точок перегину функція немає.
5. Дана функція не є парною і не є непарною. Її графік наведено на Рис. 3.6.






 40 y
40 y
 30
30
 20
20


 10
10  1-
1-  0
0




 0
0  1 x
1 x

 -10 1+
-10 1+ 
 -20
-20
 -30
-30













 -40
-40
-2 -1 0 1 2 3
Рис. 3.6. Графік функції 
Функція двох змінних. Частинні похідні.
Градієнт функції.
Нехай задано закон 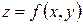 , за яким кожній впорядкованій парі незалежних змінних
, за яким кожній впорядкованій парі незалежних змінних  ставиться у відповідність хоча б єдине число z. Число z називають значенням функції f у точці
ставиться у відповідність хоча б єдине число z. Число z називають значенням функції f у точці  .
.
Приклад 1. Розглянемо функцію двох змінних  . Область визначення цієї функції - це множина усіх точок, які задовольняють нерівність
. Область визначення цієї функції - це множина усіх точок, які задовольняють нерівність 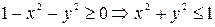 (рівняння кола радіусом 1 з центром у початку координат). Множиною значень даної функції є відрізок
(рівняння кола радіусом 1 з центром у початку координат). Множиною значень даної функції є відрізок  .
.
Нехай функція  визначена у деякому околі точки
визначена у деякому околі точки  . Тоді частинна похідна цієї функції за змінною x (або y) визначається як звичайна похідна функції однієї змінної x (або y) за фіксованого значення змінної y (або x) і позначається так (частинна похідна першого порядку):
. Тоді частинна похідна цієї функції за змінною x (або y) визначається як звичайна похідна функції однієї змінної x (або y) за фіксованого значення змінної y (або x) і позначається так (частинна похідна першого порядку):  .
.
Приклад 2. Знайти частинні похідні першого порядку від функції  .
.
 .
.
Приклад 3. Знайти частинні похідні другого порядку від функції  .
.
Для цього знайдемо спочатку частинні похідні першого порядку:
 .
.
Далі отримуємо:


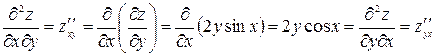 .
.
Зауваження. Похідні 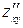 і
і  називаються мішаними частиннимипохідними.
називаються мішаними частиннимипохідними.
Для характеристики швидкості зміни функції в точці  у напрямку деякого одиничного вектора
у напрямку деякого одиничного вектора  зручно ввести поняття похідної за напрямком:
зручно ввести поняття похідної за напрямком:
 . (19)
. (19)
Приклад 4. Обчислити похідну функції  у точці
у точці  за напрямком вектора
за напрямком вектора  , де А - точка з координатами
, де А - точка з координатами  .
.
Спочатку знайдемо координати одиничного вектора  , який задає напрямок
, який задає напрямок  :
:
 . Далі обчислимо частинні похідні функції z у точці
. Далі обчислимо частинні похідні функції z у точці  :
:
 .
.
За формулою (19) маємо:  .
.
Градієнтом функції 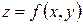 називається вектор, який у декартовій системі координат визначається за формулою:
називається вектор, який у декартовій системі координат визначається за формулою:
 . (20)
. (20)
Зауваження. У просторі градієнт функції  визначається за такою формулою:
визначається за такою формулою:
 .
.
З урахуванням виразу (20) формулу (19) можна переписати так
 ,
,
де  - кут між векторами
- кут між векторами  і
і  . Звідси випливає, що похідна функції за напрямком має найбільшу величину при
. Звідси випливає, що похідна функції за напрямком має найбільшу величину при 
 , тобто коли напрямок вектора
, тобто коли напрямок вектора  збігається з напрямком вектора
збігається з напрямком вектора  .
.
Отже, градієнт функції  у точці
у точці  характеризує напрямок і величину максимальної швидкості зростання цієї функції в даній точці.
характеризує напрямок і величину максимальної швидкості зростання цієї функції в даній точці.






