Рівняння, що описується цим законом є узагальненням 2-го закону Ньютона для суцільного середовища. Його можна записати як і для лінійних так і для нелінійних законів фільтрації. Запишемо рівняння переносу кількості руху для лінійного закону фільтрації(Дарсі).
;
Об’ємна витрата рідини через породу прямо пропорційна втраті напору рідини 
на відстані 
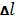і плоці фільтрації 
.
;
;
,
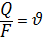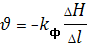z - геометрична висота положення по відношенню до деякої точки;
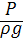- п’єзометрична висота положення по відношенню до деякої точки.
,
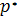- зведений тиск (дальше в системі використовуємо тільки зведений тиск)
.
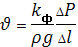Знайдемо границю:
;
;
;
= 
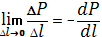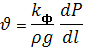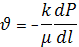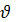x i+ y j+ z k;
;
;
;
.
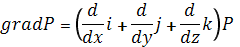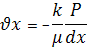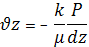Ці рівняння властиві тільки для ізотропного середовища, тобто середовища, у якого фізичні властивості у всіх напрямках однакові. Для анізотропного середовища вектори не збігаються за напрямками.
Контрольні запитання
1) Виведемо рівняння нерозривності.
2) Виведемо рівняння переносу кількості руху.
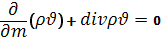
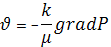
Рівняння Ейлера стосовно до рідин, що рухаються виражає другий закон Ньютона згідно якого зміна кількості руху пропорційна силі, що викликає рух і діє в напрямку дії цієї сили
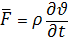
Рівняння Жуковського базується на рівнянні Ейлера з врахуванням сили опору потоку, що виникає при взаємодії рідини зі скелетом породи
Рівняння збереження енергії
Енергія – загальна кількісна міра руху і взаємодії всіх видів матерії. Енергія не виникає з нічого, а тільки переходить з однієї форми в іншу. Рівняння збереження енергії є наслідком одного з основних законів природи:енергія зберігається в ізольованій системі і може переходити з однієї форми в іншу при збереженні її кількості. Якщо система неізольовано, то її енергія може змінюватися: при одночасній зміні енергії навколишніх тіл на ту ж величину; при зміні енергії взаємодії з навколишніми тілами, або за рахунок зміни енергії взаємодії самих тіл на ту ж величину.
Для введення рівняння збереження енергії виділимо в поровому просторі деякий елементарний об’єм.
Зміна енергії dE деякого порового об’єму дорівнює роботі зовнішніх сил dA і притоку (відтоку) певної кількості теплоти dQ.
dE=dA+dQ;
;
,
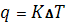де K- емпіричний коефіцієнт;
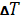- термічна температура;
T- температура в системі.
Рівняння стану
Рівняння стану використовується для спрощення диференціальних рівнянь. При русі суцільного середовища спостерігається зміна параметрів стану (Р, Т), що впливає на фізичні властивості як самого середовища так і пластового флюїду, що його насичує.
a=a(T,P)
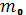=m- коефіцієнт об’ємного розширення скелету.
- коеф. об’ємної пружності середовища
Крайові умови
Призначені забезпечувати існування і єдність розв’язку. Кількість крайових умов визначається типом диференціального рівняння, а їх вигляд: умовами на границях пластових систем і початковим станом.
Початкові умови – задаються у випадку, коли розглядається нестаціонарно задача, їх кількість рівна порядку похідної по часу шуканої функції.
Р(r=0)=Pm.
Граничні умови – як правило задаються на границі пласта (покрівля, підошва). З математичної точки зору граничні умови задають характер зміни в часі шуканої функції на границі S деякої області D. Існують різні способи задання граничних умов.
Статично на границі S задаються відповідні поверхневі сили.
Кінематично на границі S задаються швидкості точок, що умовно описують фільтраційний рух.
Змішано на одних ділянках статично, на цілих кінематично.
В задачах руху рідин і газів використовують змішані граничні умови.
Граничні умови поділяють на 1-го і 2-го роду.
1-го роду – це значення самої функції на границі пласта Pn=Po
2-го роду- це значення похідної шуканої функції на границі пласта.
Контрольні запитання
1) Рівняння нерозривності фільтраційного потоку.
2) Рівняння переносу кількості руху.
3) Вивід лінійного закону Дарсі.
4) Рівняння збереження енергії.
5) Рівняння стану.
6) Поняття початкових і граничних умов.
7) Принципи моделювання пластових систем.
Лекція 4
