Будь – яке явище чи процес завершує своє дослідження при математичному моделюванні оптимізацією значень тих чи інших параметрів. Досліджувана функція, що залежить від цих параметрів може набувати максимальне або мінімальне значення в залежності від постановки конкретної задачі. Значення самих параметрів тісно зв’язані з критерієм оптимальності, який обумовлюється на початку задачі.
Оптимізаційні задачі широко застосовують в інженерній практиці, починаючи від простіших до більш складніших.
На значення досліджуваних параметрів впливають фізико – хімічні властивості процесів, а також технічні і технологічні характеристики. В загальному, будь – яка оптимізаційна задача включає:
Функція мети або критерій оптимальності.
Область допустимих значень параметрів, що задається системою обмежень на значення цих параметрів
Деякі додаткові дані щодо досліджуваних параметрів
Розглянемо загальний вид оптимізаційної задачі:
1) 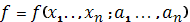
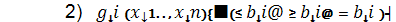
3) 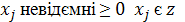
j= 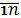
Оптимізаційні задачі за методами їх розв’язувань поділяються на 2 види:
Задачі які застосовують теорію диференціального числення
Задачі які застосовують методи математичного програмування
За своєю обстановкою оптимізаційні задачі поділяються на: задачі умовної і безумовної оптимізації. В залежності від кількості застосованих критеріїв оптимальності розрізняють: одно – і багатокритеріальні задачі.
Задачі безумовної оптимізації.
1)f=f(x) 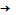 extr
extr
Для дослідження функцій застосовують необхідну і достатню умову extr. Нехай функція f(x) двічі неперервна диференційована в деякій області D.
Тоді, якщо деякій точці х*є D вона досягає екстремумy, то f’(x*)- не існує. Якщо f’’(x*)>0,то х*- min, якщо f’’(x*)<0,то х*- max.
Достатню умову екстремуму застосуємо виходячи із властивості матриці Гессе.
Якщо всі мінори матриці Гессе додатні, то х*- точка min функції.

(лек13)
Умовна оптимізація
Аналогічно як у випадку безумовної оптимізації задаємо задачу.
F=F(x,a) 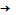 extr
extr

Cкладемо допоміжну функцію Лагранжа:
m- кількість додаткових умов
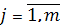
Згідно необхідної умови екстремуму
Перевірку на екстремум отриманої критичної точки здійснюємо зо допомогою властивостей матриці Гессе
Розв’язування оптимізаційних завдань з використанням методів математичного програмування.
Будь – яка задача математичного програмування включає в себе функцію мети, систему обмежень і при потребі додаткові умови на керуючі змінні. Якщо функція мети або будь - яка із функцій системи обмежень є нелінійною то ми маємо справу із задачами нелінійного програмування. За допомогою системи обмежень додається область допустимих розв’язків задачі, що геометрично зображується за допомогою так званого многокутника розв’язків.
Вершини многокутника розв’язків – допустимі розв’язки задачі лінійного програмування. Для задачі нелінійного програмування допустимі розв’язки знаходяться в будь – якій точці, обмеженій многокутником розв’язків.
Для задачі лінійного програмування множина розв’язків – це опукла, замкнута, обмежена множина точок множини. Для задач лінійного програмування многокутник розв’язків необов’язково опукла множина розв’язків. Задача розв’язків не має якщо система обмежень є несумісною, тобто функція мети – необмежена.
Серед методів розв’язку задач лінійного програмування виділяють: необмежений,метод Ньютона, метод пол. ділення, метод січних Універсальних аналогій.
Якщо в задачі будь – яка з функцій залежить від двох змінних,задачу можна розв’язати зо допомогою графічного методу.
Пр.1
Опорною прямою називають пряму, яка знаходиться по одну сторону від многокутника розв’язків і має з ним принаймні одну спільну точку.
Розглядають різні форми задач лінійного програмування:
(лек 14)






