При розв’язуванні будь – якої задачі математичного моделювання виникає питання про визначення впливу однієї змінної на інші, а також про взаємозв’язок між змінними, задіяними в даній задачі. Розглянемо найпростіший випадок
х – незалежна змінна
у – залежна змінна
 - функціональний зв'язок (простий)
- функціональний зв'язок (простий)
Однак, при описанні складних фізичних процесів чи явищ зв’язки між змінними значно складніші і представляють собою складну функціональну залежність.
Для зручності складний взаємозв’язок між змінними апроксимують зо допомогою простих зв’язків певного степеня.
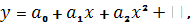 тобто згладжують деяку функціональну залежність.
тобто згладжують деяку функціональну залежність.
Існують дві схеми зв’язків:
1.Звязок між випадковою змінною у і невипадковою змінною х. Такий зв'язок носить назву регресійна залежність.
2.Між двома величинами х і у. Зв'язок між ними називається кореляційна залежність.
Регресійний аналіз
Значення невипадкової змінної х наперед відомі. І в залежності від значення х змінна у набуває або не набуває випадкового значення. При регресійних зв’язках природу випадкової величини у можна пояснити двома причинами:
В ході проведених досліджень ми можемо допуститися деякої випадкової помилки вимірювань, а змінна х вимірюється без всяких помилок.
На значення випадкової змінної у можуть впливати суб’єктивні фактори незалежні від нас. А тому в результаті при кожному фіксованому значенні х значення залежної змінної у підлягає деякому випадковому розс.
При регресійному аналізі випадкова величина у представлена к сумі двох доданків: перший – невипадкова величина, другий – випадкова величина,
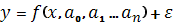



Кореляційний аналіз
х і у обидві випадкові величини; (х;у) – двохвимірна випадкова величина


 - умовне математичне сподівання
- умовне математичне сподівання
Кореляційний аналіз – це сукупність методів, які дозволяють побудувати відповідну залежність між випадковими величинами х і у, знайти оцінку параметрів цієї залежності, оцінити точність обчислень і встановити степінь зв’язку між змінними.
Нехай заданий випадковий вектор (х;у) який набуває значення представлені у вигляді множини пар точок 
Знайдемо:
Випадкова кореляція:
Парна кореляція:
Якщо за абсолютною величиною  , то ми говоримо про те, що х і у езалежні між собою.
, то ми говоримо про те, що х і у езалежні між собою.
Якщо за абсолютною величиною  1, то у – випадкова величина, залежить від іншої випадкової величини х.
1, то у – випадкова величина, залежить від іншої випадкової величини х.
Лінійна регресія.
Часто зустрічаються випадки, коли одна з двох зв’язаних між собою величин розглядається як аргумент функціональної залежності. Тобто вивчається деяка змінна величина при конкретному значенні аргументу. Представимо таку залежність у вигляду аналогічного виразу, невідомими для якого є числові параметри.
Розглянемо спрощений випадок, коли в ході досліджень є тільки одна незалежна змінна х.
y=f(x;a;b)
Нехай маємо випадок лінійної регресії у=ах+b
Для знаходження параметрів a i b застосуємо відомий метод найменших квадратів. При проведенні досліджень зв’язків можлива поява випадкової помилки обчислень, тобто 
Задача полягає в мінімізації квадрату помилки обчислень
Функція розподілу, властивості функції розподілу, щільність розподілу і її властивості
Нормальний і логарифмічно – нормальний розподіл. Числові характеристики.
Ймовірність попадання нормального розподілу випадкової величини в 
Крива Гауса(крива щільності розподілу) Властивості кривої
Генеральна і вибіркова сукупність. Види ознак впорядкування елементів вибірки
Варіаційний ряд. Розмах варіацій. Кількість інтервалів. Довжина інтервалів. Гістограма частот
Емпірична функція розподілу. Її властивості
Поняття нульової, конкуруючої гіпотези. Що таке статистична гіпотеза
Приклади типових задач щодо висунення статистичних гіпотез.
Статистичний критерій. Ступінь відмінності між емпіричним і теоретичним розподілом.
Вагома відмінність.  - рівень вагомості
- рівень вагомості
Результати перевірки статистичної гіпотези
12.1 Гіпотеза про 
12.2  - невідоме, критерій Стьюдента, Фішера
- невідоме, критерій Стьюдента, Фішера
13. Поняття статистичного аналізу зв’язків
Дві основні схеми аналізу залежностей: регресія, кореляція
14.Регресійний аналіз, кореляційний аналіз
15. Лінійна регресія, визначення параметрів.
Лекція 8
Чисельні методи
Лекція 9






