Нормальный вид квадратичной формы
Для действительной квадратичной формы
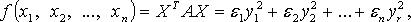
где  r = rank A.
r = rank A.
Для комплексной квадратичной формы

r = rank A.
Для действительных квадратичных форм имеет место закон инерции квадратичных форм: число положительных и число отрицательных квадратов в нормальном виде квадратичной формы не зависит от способа приведения квадратичной формы к нормальному виду с помощью невырожденных линейных преобразований.
Классификация действительных квадратичных форм
Положительно-определенные
Квадратичные формы, для которых  таких, что
таких, что 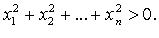 Нормальный вид
Нормальный вид 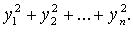 Квадратичная форма является положительно-определенной тогда и только тогда, когда все ее главные миноры положительны
Квадратичная форма является положительно-определенной тогда и только тогда, когда все ее главные миноры положительны  (критерий Сильвестра).
(критерий Сильвестра).
Отрицательно-определенные
Квадратичные формы, для которых  таких, что
таких, что 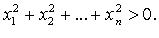 Нормальный вид Квадратичная форма является отрицательно-определенной тогда и только тогда, когда
Нормальный вид Квадратичная форма является отрицательно-определенной тогда и только тогда, когда 
Положительно-полуопределенные
Квадратичные формы, для которых  таких, что
таких, что 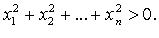 Нормальный вид
Нормальный вид  r < n, r = rank A.
r < n, r = rank A.
Отрицательно-полуопределенные
Квадратичные формы, для которых  таких, что
таких, что 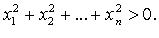 Нормальный вид
Нормальный вид 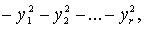 r < n, r = rank A.
r < n, r = rank A.
Неопределенные
Квадратичные формы, которые принимают как положительные, так и отрицательные значения. Нормальный вид:  r = rank A.
r = rank A.
Сравнения по модулю и их свойства
Сравнимые числа
Говорят, что целое число  сравнимо с целым числом
сравнимо с целым числом  по модулю
по модулю  , где
, где  — целое число, большее
— целое число, большее  , если разность
, если разность  делится на
делится на  без остатка.
без остатка.
Или, что то же самое, если числа  и
и  имеют одинаковый остаток от деления на
имеют одинаковый остаток от деления на  .
.
Из определения следует, что если  сравнимо с
сравнимо с  по модулю
по модулю  , то и
, то и  сравнимо с
сравнимо с  по тому же модулю
по тому же модулю  . Поэтому говорят просто, что числа
. Поэтому говорят просто, что числа  и
и  сравнимы по модулю
сравнимы по модулю  .
.
Обозначение:  . Знак
. Знак  (сравнимо) по начертанию совпадает со знаком "тождественно равно", но по смыслу не имеет с ним ничего общего.
(сравнимо) по начертанию совпадает со знаком "тождественно равно", но по смыслу не имеет с ним ничего общего.
Примеры:  . Иногда удобно записывать цепочку сравнений. Тогда модуль указывается один раз в конце цепочки:
. Иногда удобно записывать цепочку сравнений. Тогда модуль указывается один раз в конце цепочки:  .
.
Сравнение
Запись  , где
, где 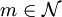 ,
,  , называется сравнением (сравнением первой степени) и означает, что число
, называется сравнением (сравнением первой степени) и означает, что число  сравнимо с числом
сравнимо с числом  по модулю
по модулю  .
.
Свойства сравнений
1. Сравнимость с нулём.  сравнимо с
сравнимо с  по модулю
по модулю  , тогда и только тогда, когда
, тогда и только тогда, когда  делится на
делится на  .
.  .
.
2. Рефлексивность.  для любого целого
для любого целого  .
.
3. Симметричность. Для любых целых  и
и  верно:
верно: 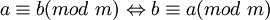 .
.
4. Транзитивность. Для любых целых  ,
,  и
и  верно:
верно:  .
.
5. Аддитивность. Если  и
и  , то
, то 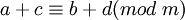 .
.
6. Мультипликативность. Если  и
и  , то
, то  .
.
7. Умножение модуля. Если  и
и  и
и 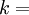 НОК
НОК  , то
, то  .
.
8. Правила сокращения для сравнений следующие.
· Можно делить обе части сравнения на число, взаимно простое с модулем: если 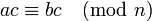 и
и  , то
, то 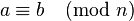 .
.
· Можно одновременно разделить обе части сравнения и модуль на их общий делитель: если  , то
, то 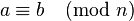 .
.
Классы вычетов
Множество всех чисел сравнимых с a по модулю n называется классом вычетов a по модулю n, и обычно обозначается  или
или  . Таким образом, сравнение
. Таким образом, сравнение 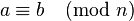 равносильно равенству классов вычетов
равносильно равенству классов вычетов  .
.




