Внутриземных источников
Решая задачу аналитической оценки параметров B 0, представим модель главного поля рядами сферических гармоник в зависимости от географических координат.
Скалярный потенциал индукции ГМП внутриземных источников U [нТл·км] в точке пространства со сферическими координатами r, θ, λ определяется выражением
 (1)
(1)
где r – расстояние от центра Земли до точки наблюдения (геоцентрическое расстояние), [км]; λ – долгота от Гринвичского меридиана, [градусы]; θ – полярный угол (дополнение до широты,
θ = (π/2) – φ’, [градусы], где φ’ – широта в сферических координатах, [градусы]); R З – средний радиус Земли, R З = 6371.03, [км]; gnm (t), hnm (t) – сферические гармонические коэффициенты, [нТл], зависящие от времени; Pnm – нормированные по Шмидту присоединенные функции Лежандра степени n, порядка m [5].
В геофизической литературе выражение (1) широко известно как ряд Гаусса и общепризнано в качестве международного эталона невозмущенного состояния ГМП.
Несмотря на большое число выполненных сферических гармонических анализов, вопрос об оптимальной длине сферического гармонического ряда на сегодняшний день остается открытым. Чтобы выяснить значение членов высоких порядков, Г. Фанзелау вычислил коэффициенты gnm и hnm до 15 порядка, В. Колесова и Э. Кропачев – до 23 порядка.
Основное, что следует из анализа этих данных, – это резкое уменьшение всех коэффициентов для 6–8 порядков и затем медленное убывание их с некоторыми колебаниями. При этом ни у одного коэффициента, вплоть до 23го порядка, нет резкого увеличения, что указывало бы на источники магнитного поля локального характера.
Таким образом, анализы с большим числом членов подтверждают предположение Гаусса о сходимости сферического гармонического ряда, представляющего геомагнитный потенциал. Обычно при сферических гармонических анализах ряды ограничиваются 8–10 членами. Однако при достаточно однородных и высокоточных исходных данных, какие, например, получаются при спутниковых съемках, возможно продление рядов до 12
и 13 гармоник. Коэффициенты гармоник более высоких порядков по величине сравнимы или меньше погрешности определения коэффициентов.
Так, к примеру, при длине ряда 11–13 гармоник погрешность вычисления ГМП на поверхности Земли не превышает ~2 %.
По причине временных вариаций главного поля коэффициенты гармонических рядов (сферические гармонические коэффициенты) периодически (раз в 5 лет) пересчитывают с учетом новых экспериментальных данных. Изменения главного поля за один год или так называемый вековой ход также представляются рядами сферических гармоник, которые доступны на веб-ресурсе: http://www.geomagnet.ru/igrf12coeffs.txt.
Нормированные по Шмидту присоединенные функции Лежандра Pnm, заявленные в выражении (1), представляют собой в общем случае ортогональный многочлен, имеющий вид выражения
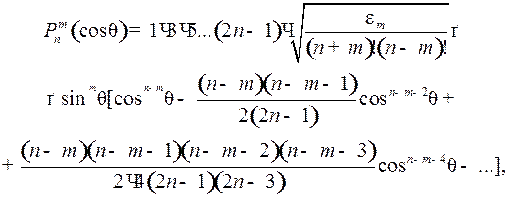 (2)
(2)
где εm – нормировочный множитель (εm = 2 для m ≥ 1 и εm = 1 для
m = 0); n – степень сферических гармоник; m – порядок сферических гармоник.
Методика расчета невозмущенного ГМП представлена на рис. 2 [1].
Таким образом, распределение вектора индукции ГМП в пространстве характеризуется следующим набором геомагнитных элементов:
§ прямоугольные составляющие ГМП;
§ модуль вектора индукции ГМП;
§ угловые элементы ГМП (геомагнитного диполя).
Как правило, в определенных научных задачах некоторые геопространственные данные (например, положения искусственных спутников Земли в пространстве) представляют в географических (геодезических) координатах φ, λ, h, основанных на аппроксимации поверхности Земли эллипсоидом вращения. При этом в задачах иного рода в первом приближении эллиптичностью Земли пренебрегают, не делая разницы между сферическими и геодезическими координатами. Однако при точных расчетах желательно учитывать полюсное сжатие Земли.

Рис. 2. Методика расчета параметров невозмущенного ГМП
Так, учитывая такого рода сжатия, r и φ’ будут вычисляться согласно следующим выражениям соответственно:
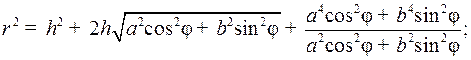 (3)
(3)
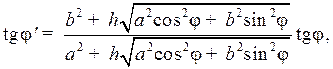 (4)
(4)
где φ – географическая (геодезическая) широта точки в пространстве, [градусы]; h – высота точки над уровнем моря, [градусы]; a – большая полуось земного эллипсоида вращения; b – малая полуось земного эллипсоида вращения.
Учитывая, что долготы λ в сферических и геодезических координатах тождественны, составляющие вектора индукции ГМП внутриземных источников X ’, Y ’, Z ’ в нТл определятся как:



Так, в точке A (φ, λ, h) прямоугольные составляющие вектора индукции (в геодезической системе координат) определятся согласно выражениям (5)–(8), а модуль вектора индукции ГМП – по формуле (9).
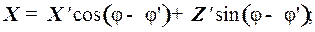 (5)
(5)
 (6)
(6)
Значения элемента поля Y для точки пространства при θ = 0 получают линейной интерполяцией.
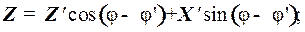 (7)
(7)
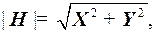 (8)
(8)
где | H | – горизонтальная составляющая вектора индукции ГМП B 0(проекция B 0на горизонтальную плоскость XY)
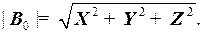 (9)
(9)
Угловые элементы геомагнитного диполя определим
из следующих соотношений:
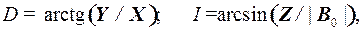
где D – магнитное склонение, т. е. угол между географическим и магнитным меридианами (положительное к востоку); I – магнитное наклонение, т. е. угол между горизонтальной плоскостью XY и вектором B 0 (положительное к востоку).
При расчете геомагнитных элементов на заданный год t сферические гармонические коэффициенты gnm (t)и hnm (t)необходимоактуализировать в соответствии с выражениями (10) и (11) соответственно:
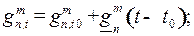 (10)
(10)
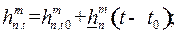 (11)
(11)
где t – текущий год; t 0 – год, на который известны сферические гармонические коэффициенты gnm (t), hnm (t); g nm и h nm – поправка на сферические гармонические коэффициенты, связанная с вековым ходом ГМП.
Дипольное геомагнитное поле (рис. 1) соответствует полю, представленному первым членом сферических гармоник. Составляющие дипольного члена рассчитываются по формулам:



Координаты полюсов дипольного поля (геомагнитных полюсов) и его магнитный момент M [Тл·м3] находятся из выражений
(12)–(14) соответственно.
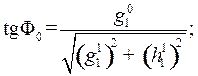 (12)
(12)
 (13)
(13)
 (14)
(14)
где Ф0 и Λ0 – географическая широта и долгота геомагнитного полюса соответственно, [градусы].
На ресурсе http://www.geomagnet.ru/WMM/index.html представлен вариант программной формализации модели World Magnetic Model (WMM) в виде специализированного калькулятора расчета параметров ГМП. Под WMM понимают стандартную модель расчета параметров ГМП, признанную и широко используемую по всему миру, в том числе Российской академией наук, Министерством обороны США, Британским геологическим обществом (BGS), Организацией cсевероатлантического альянса (NATO), Национальным управлением океанических и атмосферных исследований (NOAA) и др.
Отклонения фактически наблюдаемых параметров ГМП от расчетных значений чаще всего относят к геомагнитными вариациями (ГМВ) различной природы происхождения. В настоящее время специалисты в области геофизики, геологии, космонавтики, медицины, целого ряда технических наук и многих других сфер научных знаний уделяют все большее внимание сопоставлению параметров внешних ГМВ с тенденциями существования и развития под их влиянием объектов и систем различной природы происхождения, анализу полученных результатов и выявлению соответствующих закономерностей [1, 6–7].
Задание на лабораторную работу
2.1. С помощью сервиса «Geomagnetic Calculator» веб-портала GEOMAGNET (http://www.geomagnet.ru) определить текущие географические координаты lat0, long0, alt0, (где lat0 – географическая широта, long0 – географическая долгота, alt0– высота над уровнем моря), а также основные параметры геомагнитного поля (ГМП) внутриземных источников в точках с координатами:
§ lat0, long0, alt0;
§ lat0, long0, (alt0 + Δalt);
§ lat0, long0, (alt0 + 2·Δalt);
§ lat0, long0, (alt0 + 3·Δalt),
где Δalt = 4000 м.
Построить графические зависимости Bx (alt), By (alt), Bz (alt), B (alt) и объяснить полученные результаты.
2.2. Построить графическую зависимость изменения параметра полного вектора индукции главного поля от параметра географической широты B (lat) вдоль меридиана 120 ° в. д.
с шагом 10 °. Объяснить полученный результат.
2.3. Построить графическую зависимость изменения параметра полного вектора индукции главного поля от параметра географической долготы B (long) вдоль параллели 65 ° с. ш.
с шагом 10 °. Объяснить полученный результат.
2.4. Определить параметры магнитного склонения и магнитного наклонения для следующих географических объектов:
мыс Челюскина; г. Норильск; г. Мурманск; г. Москва; г. Нью-Йорк;
г. Рио-де-Жанейро; г. Кейптаун; г. Пунта-Аренас.
2.5. Ответить на контрольные вопросы и оформить отчет
о проведенных исследованиях в соответствии с действующим стандартом организации.
Ход выполнения работы
3.1. Загрузить веб-портал GEOMAGNET (http://www. geomagnet.ru), запустить сервис «Geomagnetic Calculator» и ознакомиться с функционалом пользовательского интерфейса.
3.2. Определить текущие географические координаты:
§ lat0 (географическая широта),
§ long0 (географическая долгота),
§ alt0 (высота над уровнем моря).
Интегрированная в сервис «Geomagnetic Calculator» функция геолокации обеспечивает автоматическое определение географических координат пользовательского устройства и при загрузке сервиса рассчитывает комплекс параметров главного поля для данной точки. Географические координаты также можно определить, указав на карте текущее местоположение (или введя его название в адресное поле).
3.3. Определить основные параметры ГМП внутриземных источников в точках ({lat0, long0, alt0};
{lat0, long0, (alt0 + Δ alt}; {lat0, long0, (alt0 + 2·Δ alt)}; {lat0, long0, (alt0 + + 3·Δ alt)}, где Δ alt = 4000 м), изменяя значения в соответствующем поле ввода пользовательского интерфейса. Полученные значения занести в табл. 2.
Таблица 2
Параметры ГМП в точке, заданной географическими координатами
| Параметр | Значения | |||
| Высота над уровнем моря, м | ||||
| alt0 | alt0+Δ alt | alt0+2·Δ alt | alt0+3·Δalt | |
| Географическая широта lat0, град | ||||
| Географическая долгота long0, град | ||||
| Сев. комп. индукц. ГМП: Bx, нТл | ||||
| Вост. комп. индукц. ГМП: By, нТл | ||||
| Верт. комп. индукц. ГМП: Bz, нТл | ||||
| Полный вектор индукц. ГМП: B, Тл | ||||
| Магнитное склонение D, град. | ||||
| Магнитное наклонение I, град. |
3.4. Построить графические зависимости компонент ГМП от параметра высоты над уровнем моря: Bx (alt), By (alt), Bz (alt), B (alt). Объяснить полученные результаты и сделать выводы.
3.5. Установить значение меридиана в соответствующем поле ввода пользовательского интерфейса равным 120 ° в.д. Изменяя значение географической широты в диапазоне ±90 ° с шагом 10 °, регистрировать значение параметра полного вектора индукции главного поля. Результаты наблюдений представить в виде таблицы
и построить графическую зависимость полного вектора магнитной индукции главного поля от параметра географической широты. Проанализировать полученный характер распределения и сделать выводы.
3.6. Установить значение географической широты в поле ввода пользовательского интерфейса равным 65 ° в.д. Изменяя значение географической долготы в диапазоне ±180 ° с шагом 10 °, регистрировать значение параметра полного вектора индукции главного поля. Результаты наблюдений представить в виде таблицы и построить графическую зависимость полного вектора магнитной индукции главного поля от параметра географической долготы. Проанализировать полученный характер распределения и сделать выводы.
3.7. В поле поиска пользовательского интерфейса сервиса «Geomagnetic Calculator» ввести название географического объекта (табл. 3). Зарегистрировать значения географической широты и долготы, углы магнитного склонения D и наклонения I, внести результаты в табл. 3. Проанализировать полученные данные и сделать выводы.
Таблица 3
Магнитное склонение и магнитное наклонение
| Параметр Географ. объект | Широта lat0, град | Долгота long0, град | Высота над уровнем моря alt, км | Угол магнитного склонения D, град | Угол магнитного наклонения I, град |
| мыс Челюскина | |||||
| г. Норильск | |||||
| г. Мурманск | |||||
| г. Москва | |||||
| г. Нью Йорк | |||||
| г. Рио-де-Жанейр | |||||
| г. Кейптаун | |||||
| г. Пунта-Аренас |
Контрольные вопросы
1. Что обуславливает существование ГМП?
2. Что такое нормальное (невозмущенное) ГМП и каким образом можно определить его параметры?
3. В каких пределах изменяется полный вектор индукции главного поля на поверхности Земли?
4. Для чего необходимо пересчитывать сферические гармонические коэффициенты и с какой периодичностью их принято пересчитывать?
5. Каким образом при расчете параметров ГМП учитывается эллиптичность Земли?
6. Перечислите основные параметры ГМП.
7. Дайте определение угловым элементам ГМП.
8. В каких областях народного хозяйства и с какой целью необходимо вести контроль и анализ параметров ГМП и его вариаций?
9. Какие информационные ресурсы для расчета и анализа параметров ГМП Вам известны?
Список литературы
1.Воробьев А. В., Шакирова Г. Р., Иванова Г. А., Кильметов Э. А. Теория и практика создания информационных систем специального назначения: монография. Уфа: Уфимск. гос. авиац. техн. ун-т, 2015. С. 44– 58.
2. Короновский Н. В. Магнитное поле геологического прошлого Земли // Соросовский образовательный журнал №6, 1996 г. С. 65-73.
3. ГОСТ 25645.126-85. Поле геомагнитное. Модель поля внутреземных источников. М.: Изд-во стандартов, 1985.
4. ГОСТ 25645.127-85. Магнитосфера Земли. Модель магнитного поля магнитосферных токов. М.: Изд-во стандартов, 1985.
5. Die Darstellung des geomagnetichen Potentials zur Epoche 1945 durch eine Entwicklung nach Kugelfunktionen bis zur 15 Ordung / G. Fanselan [et al.] // Pure a. Appl. Geophys. 1964. Vol. 57. P. 5–30.
6.Воробьев А. В., Шакирова Г. Р., Иванова Г. А. Исследование и анализ естественных факторов, воздействующих на метрологические характеристики магнитометричес-ких инклинометров // Вестник УГАТУ, Том 19 №1 (67), 2015 г. С. 107-115.
7. Воробьев А. В., Шакирова Г. Р., Иванова Г. А.Система принятия решения для гибридной инклинометрической системы на основе технологии картографического веб-сервиса// Фундаментальные исследования. 2015. № 5 (часть 2). C. 260-264.
8. Пантелеев В. Л. Теория фигуры Земли: курс лекций. М.: Изд-во МГУ. С. 35–40.
9. Кампе де Ферье Ж. Функции математической физики. Справочное руководство. М.: Гос. изд-во физико-математической литературы, 1963. С. 42–43.






