Определение: Статистической гипотезой называется всякое непротиворечивое множество утверждений {Н0, Н1, …, Hk-1} относительно свойств распределения случайной величины. Любое из утверждений Hi называется альтернативой гипотезы. Простейшей гипотезой является двухальтернативная {H0, H1}. В этом случае альтернативу H0 называют нулевой гипотезой, а H1 - конкурирующей гипотезой.
Определение: Критерием называется случайная величина 
, которая позволяет принять или отклонить нулевую гипотезу H0.
При проверке гипотез можно допустить ошибки двух родов.
Ошибка первого рода состоит в том, что будет отклонена гипотеза H0, если она верна ("пропуск цели"). Вероятность совершить ошибку первого рода обозначается α и называется уровнем значимости. Наиболее часто на практике принимают, что α = 0,05 или α = 0,01.
Ошибка второго рода заключается в том, что гипотеза H0 принимается, если она неверна ("ложное срабатывание"). Вероятность ошибки этого рода обозначается β.
Определение: Критерием согласия называется критерий проверки гипотезы о предполагаемом законе распределения.
Критерий согласия 
Это один из наиболее часто применяемых критериев. Алгоритм проверки гипотезы следующий.
1. Построить гистограмму равновероятностным способом.
2. По виду гистограммы выдвинуть гипотезу
,
,
где f0(x) - плотность вероятности гипотетического закона распределения: равномерного, экспоненциального или нормального.
Замечание. Гипотезу об экспоненциальном законе распределения можно выдвигать в том случае, если все числа в выборке положительные.
3. Вычислить значение критерия по формуле
где 
- частота попадания в i-й интервал;
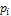- теоретическая вероятность попадания случайной величины в i- й интервал при условии, что гипотеза H0 верна.
Формулы для расчета 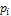в случае экспоненциального, равномерного и нормального законов соответственно равны.
Экспоненциальный закон
При этом A1 = 0, Bm = +∞.
Равномерный закон
Нормальный закон
При этом A1 = -∞, BM = +∞.
Замечания. После вычисления всех вероятностей 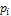проверить, выполняется ли контрольное соотношение
4. Из таблицы "Хи-квадрат" приложения выбирается значение 
, где α - заданный уровень значимости (α = 0,05 или α = 0,01), а k - число степеней свободы, определяемое по формуле
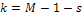
Здесь s - число параметров, от которых зависит выбранный гипотезой H0 закон распределения. Значения s для равномерного закона равно 2, для экспоненциального - 1, для нормального - 2.
5. Если 
, то гипотеза H0 отклоняется. В противном случае нет оснований ее отклонить.
Критерий согласия Колмогорова
Последовательность действий при проверке гипотезы следующая.
1. Построить вариационный ряд.
2. Построить график эмпирической функции распределения F*(x).
3. Выдвинуть гипотезу:
,
,
где F0(x) - теоретическая функция распределения типового закона: равномерного, экспоненциального или нормального.
Ниже приведены формулы для расчета F0(x).
Равномерный закон
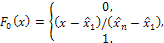
Экспоненциальный закон
Нормальный закон
4. Рассчитать по формулам 10-20 значений и построить график функции F0(x) в одной системе координат с функцией F*(x).
5. По графику определить максимальное по модулю отклонение между функциями F*(x) и F0(x).
6. Вычислить значение критерия
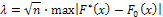
7. Принимают тот или иной уровень значимости (чаще всего 0,05 или 0,01). Тогда доверительная вероятность γ =1−α.
8. Из таблицы вероятностей Колмогорова (см. приложение) выбрать критическое значение λγ.
9. Если λ > λγ, то нулевая гипотеза H0 отклоняется, в противном случае - принимается, хотя она может быть неверна.
Достоинства критерия Колмогорова по сравнению с критерием χ2: возможность применения при очень маленьких объемах выборки (n < 20), более высокая «чувствительность» а следовательно, меньшая трудоемкость вычислений.
Недостаток: критерий можно использовать в том случае, если параметры Q1,..., Qk распределения заранее известны, а эмпирическая функция распределения F*(x) должна быть построена по несгруппированным выборочным данным.
Задание для самостоятельной работы:
Выдвинуть гипотезу о законе распределения случайной величины и проверить ее при помощи критерия согласия χ2 и критерия Колмогорова (α = 0,05).
Рекомендуемая литература: 3; 4; 5
