1 Найти неопределенный интеграл 
.
Результат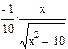 
:
2 Найти определенный интеграл 
.
Результат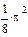 
.
3 Найти производные первого порядка 
.
Результат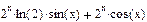 
.
4 Найти производные высокого порядка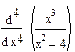 
.
Результат 
Контрольные вопросы
1 Как найти в символьном виде определенные и неопределенные интегралы?
2 Можно ли применять символьные операции к интегралам по области, к трехмерным интегралам, к контурным интегралам?
3 Можно ли в символьному виде найти производные высоких порядков?
Лабораторная работа №6
Вычисление производных в задачах геометрии и частных производных
Цель работы: вычисление производных в задачах геометрии и нахождение частных производных высоких порядков в программе MathCad.
Указания к выполнению лабораторной работы:
I Составить уравнение касательной и нормали к линии, которая задана уравнением y(x)=f(x) в точке М(x0,y0).
1 Задать значения х0 и у0 в точке М.
2 Записать уравнение линии у(х).
3 Определить производную от функции у(х)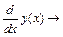 
, использовав панель вычислений и панель символов. Присвоить значение производной функции уу(х): = 
.
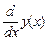4. Записать уравнение касательной у виде
,
5. Аналогично записать уравнение нормали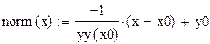 
6. Построить графики касательной и нормали.
7 Отформатировать графики.
II Выполнить числовое и символьное вычисление частных производных высшего порядка от функции трех переменных.
1 Записать функцию, от которой будут вычисляться производные второго порядка.
2 Обратиться к панели вычислений и выбрать оператор дифференцирования.
3 В соответствующем месте заполнения оператора записать функцию, переменную для дифференцирования и порядок дифференцирования.
4 Нажать правой кнопкой мыши на знак оператора дифференцирования и в контекстному меню выбрать View Derivative As (Показать производную как), установить флажок Partial Derivative (Частная производная).
5 Отметить оператор дифференцирования и обратиться к панели Символика/Вычислить/В символах.
6 Задать числовые значения для переменных, от которых вычисляется производная.
7 Вычислить числовые значения производных.
Таблица 6.1 – Варианты заданий к лабораторной работе №6
| Номер варианта | Функция f(x) для определения касательной и нормали | Точка М (х0,у0) для определения касательной и нормали | Функция f(x,у,z) для вычисления частной производной | Точка М (х0,у0,z0) для числового вычисления частной производной | ||||
| х2 -3х+5 | (2,3) | х2 -3х3y-4y2+2y-z3 | (0,1,2) | |||||
| х2 +2х+6 | (-1.1) | z2ex*x+y*y | (0,0,0) | |||||
| х3-3х2 | (3,1) | xcos(y)+yz4 | (1,0,0) | |||||
| 0.5х-sin(x) | (0, p/3) | z ln (x2-y2) | (3,1,3) | |||||
| (x-5)ex | (4,0) | zsin(xy)+z2 | (1,1,1) | |||||
| 1-(x-2)4/5 | (2,1) | х2 +2y2-3xy-4z2 | (0,0,0) | |||||
| x5+5x-6 | (0,-1) | zx× ln (y)+xy2z | (0,2,1) | |||||
| (x3+4)/x2 | (2,3) | y(x-zcos(x)) | (0,0,0) | |||||
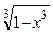
| (0,1) | sin(x)(cos(z)+cos(y)) | (1,0,0) | |||||
| sin2(x) | (0.5,0.5) | x4yz+sin(y) | (2,1,0) | |||||
| x2-0.5x4 | (0,0) | (x-y2)*(z3-x) | (1,1,1) | |||||
| х3-3х2 | (0, p/3) | х2 -3х3y-4y2+2y-z3 | (0,1,2) | |||||
| 0.5х-sin(x) | (4,0) | z2ex*x+y*y | (0,0,0) | |||||
| (x-5)ex | (2,1) | xcos(y)+yz4 | (1,1,1) | |||||
| 1-(x-2)4/5 | (2,1) | z ln (x2-y2) | (3,1,3) | |||||
| x5+5x-6 | (0,-1) | zsin(xy)+z2 | (1,1,1) | |||||
| 0.5х-sin(x) | (0, p/3) | х2 +2y2-3xy-4z2 | (0,0,0) | |||||
| (x-5)ex | (4,0) | zx× ln (y)+xy2z | (0,2,1) | |||||
Продолжение табл. 6.1
| 1-(x-2)4/5 | (2,1) | y(x-zcos(x)) | (0,0,0) | |||||
| x5+5x-6 | (0,-1) | sin(x)(cos(z)+cos(y)) | (1,0,0) | |||||
| (x3+4)/x2 | (2,3) | zx× ln (y)+xy2z | (0,2,1) | |||||
| х3-3х2 | (3,1) | y(x-zcos(x)) | (0,0,0) | |||||
| 0.5х-sin(x) | (0, p/3) | sin(x)(cos(z)+cos(y)) | (1,0,0) | |||||
| (x-5)ex | (4,0) | x4yz+sin(y) | (2,1,0) | |||||
| 1-(x-2)4/5 | (2,1) | (x-y2)*(z3-x) | (1,1,1) | |||||
| x5+5x-6 | (0,-1) | х2 -3х3y-4y2+2y-z3 | (0,1,2) | |||||
| (x3+4)/x2 | (2,3) | z2ex*x+y*y | (0,0,0) | |||||
|
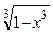
| (0,1) | xcos(y)+yz4 | (1,0,0) | |||||
| sin2(x) | (0.5,0.5) | z ln (x2-y2) | (3,1,3) | |||||
| x2-0.5x4 | (0,0) | zsin(xy)+z2 | (1,1,1) | |||||
Пример
I Составить уравнение касательной и нормали к линии, которая задана уравнением y(x)=х4 -3х3+4х2-5х+1 в точке М(0,1).
1 Задать значения х0 и у0 в точке М: х0:=0, у0:=1.
2 Записать уравнения лини у(х):= х4 -3х3+4х2-5х+1.
3 Определить производную от функции у(х) 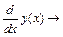, использовав панель вычислений и панель символов. Присвоить значение производной функции уу(х): = .
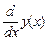4 Записать уравнение касательной в виде
,
 .
|
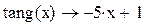5 Аналогично записать уравнение нормали
|
|
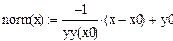
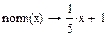
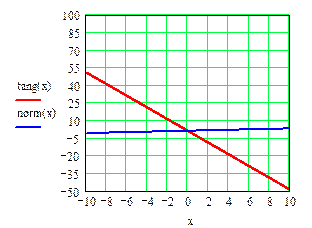
6 Построить графики касательной и нормали.
7 Отформатировать графики.
|
|
|
|
|
|
|
|
|
|
|
|
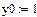
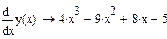
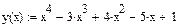
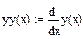
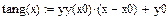
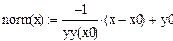
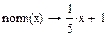
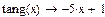
Рисунок 24- График касательной и нормали
ІІ Записать функцию, от которой будут вычисляться производные второго порядку
2 Обратиться к панели вычислений и выбрать оператор дифференцирования 
.
3 В соответствующие места заполнения оператора записать функцию, переменную для дифференцирования и порядок дифференцирования.
4 Нажать правой кнопкой мыши на знак оператора дифференцирования и в контекстному меню выбрать View Derivative As (Показать производную как), установить флажок Partial Derivative (Частная производная) (рис.25):
, 
, 
.
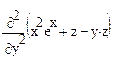5 Отметить оператор дифференцирования и обратиться к панели Символика/Вычислить/В символах.
6 Задать числовые значения для переменных, от которых вычисляется производная х:=1, y:=1, z:=1.
7 Вычислить числовые значения производных.
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
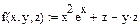
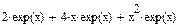
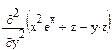
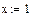
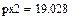
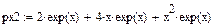
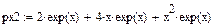
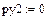
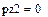
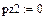
Рисунок 25 – Диалоговое окно Показать производную
Контрольные вопросы
1 Як найти касательную к любой кривой в MathCad?
2 Як найти нормаль к любой кривой в MathCad?
3 Як выполнить символьные вычисления частных производных высокого порядка?
4 Як выполнить числовые вычисления частных производных высокого порядка?
Лабораторная работа №7
Вычисление интегралов в задачах геометрии и механики
Цель работы: вычисление интегралов в задачах геометрии и механики в программе MathCad.
Указания к выполнению лабораторной работы:
I Вычислить площадь плоской фигуры, ограниченной заданными линиями.
1 Записать уравнение кривых, которые ограничивают площадь плоской фигуры.
2 Найти точки их пересечения, для того чтобы использовать их у двукратном интегрировании.
3 Обратиться на панели Символы к функции simplify.
4 Ввести оператор интегрирования. В соответствующих местах заполнить имя первой переменной и границы интегрирования.
5 На месте ввода функции под интегралом ввести еще один оператор интегрирования, границы интегрирования и подынтегральную функцию
II Вычислить координаты центру тяжести пластины.
1 Записать уравнения кривых, которые описывают область D пластины.
2 Найти точки их пересечения, для того чтобы использовать их в двукратном интегрировании.
3 Найти площадь S однородной пластинки через двойной интеграл.
3.1 Обратиться на панели Символы к функции simplify.
3.2 Ввести оператор интегрирования. В соответствующих местах заполнить имя первой переменной и границы интегрирования.
3.3 На месте ввода функции под интегралом ввести еще один оператор интегрирования, границы интегрирования и подынтегральную функцию
4 Найти аналогично статические моменты Mx и My пластины относительно осей Ох и Оу как двойные интегралы
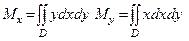
5 Определить координаты центра тяжести как отношение подынтегральной функции, которая определяет статические моменты пластины относительно осей Ох и Оу
Таблица 7.1 – Варианты задания к лабораторной работе №7
| Номер варианта | Функции для вычисления площади фигуры | Функции для вычисления координат центра тяжести фигуры |
| x=y2-2y; x+y=0 |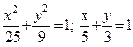 
| |
| y=2-x; y2=4x+4 | y=x2; y=2x2; x=1;x=2 | |
| y2=4x-4; y2=2x (извне параболы) | y2=x; x2=y | |
| 3y2=25x; 5x2=9y | y=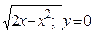 
| |
| y2+2y-3x+1=0; 3x-3y-7=0 |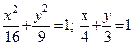 
| |
| y=4x-4x2; y=x2-5x | 
| |
| x=4-y2; x+2y-4=0 |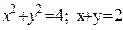 
| |
| y2=4(x-1); x2+ y2=4 (извне параболы) |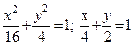 
| |
| x=y2-2y; x+y=0 |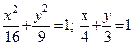
| |
| y=2-x; y2=4x+4 |
| |
| y2+2y-3x+1=0; 3x-3y-7=0 |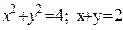
| |
| y=4x-4x2; y=x2-5x | y2=x; x2=y | |
| x=4-y2; x+2y-4=0 | y=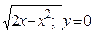
| |
| x=y2-2y; x+y=0 |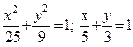
| |
| y=2-x; y2=4x+4 | y=x2; y=2x2; x=1;x=2 | |
| y2+2y-3x+1=0; 3x-3y-7=0 |
| |
| y=4x-4x2; y=x2-5x |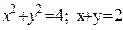
| |
| x=4-y2; x+2y-4=0 |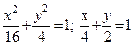
| |
| x=y2-2y; x+y=0 |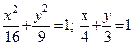
| |
| y=2-x; y2=4x+4 |
| |
| y2=4(x-1); x2+ y2=4 (извне параболы) |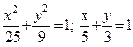
| |
| y=2-x; y2=4x+4 | y=x2; y=2x2; x=1;x=2 |
Продолжение табл. 7.1
| y2=4x-4; y2=2x (извне параболы) | y2=x; x2=y | |||
| x=y2-2y; x+y=0 | y=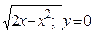
| |||
| y=2-x; y2=4x+4 |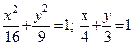
| |||
| 3y2=25x; 5x2=9y |
| |||
| x=y2-2y; x+y=0 |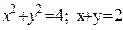
| |||
| y2+2y-3x+1=0; 3x-3y-7=0 |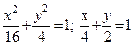
| |||
| y=4x-4x2; y=x2-5x | y=x2; y=2x2; x=1;x=2 | |||
| x=4-y2; x+2y-4=0 | y2=x; x2=y | |||
Пример
I Вычислить площадь фигуры, которая ограничена линиями x=4y-y2 и x+y=6.
1 Найти координаты точек пересечения заданных линий, для чего необходимо решить систему уравнений (одной из встроенных функций MathCad, графически или решить систему уравнений).
x=4y-y2
x+y=6.
В результате будут получены точки пересечения А(4;2) и В(3;3).
2 Записать формулу для вычисления площади через кратный интеграл и использовать на панели Символы функцию simplify
.
II Вычислить координаты центра тяжести пластины, которая ограничена кривыми y2=4x+4 i y2=-2x+4.
Площадь
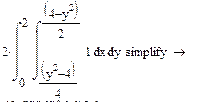
Статические моменты относительно осей Ох и Оу
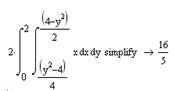
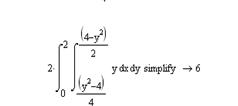
Координаты центра тяжести
Контрольные вопросы
1 Какие геометрические характеристики можно вычислить с использованием интегралов?
2 Как вычислить центр тяжести через интегралы?
Лабораторная работа №8
Решение обычных дифференциальных уравнений в MathCad
Цель работы: с использованием встроенных функций и блочной структуры найти решение обычных дифференциальных уравнений.
Указания к выполнению лабораторной работы:
I Найти решение обычного дифференциального уравнения y /= f (x,y) с использованием «блока решений».
1. Ввести ключевое слово given (дано), с которого начинается блок решений.
2. Записать уравнение, используя знак логического равенства между правой и левой частями уравнения с панели управления Evaluation (Выражения).
3. Задать начальные значения переменной, которая есть в уравнении.
4. Ввести ключевое слово Odesolve, которым заканчивается блок решений, то есть присвоить функции, относительно которой решается уравнение, значение Odesolve с параметрами интервала интегрирования.
5. Определить значение найденной функции в точках интервала, для чего создать соответствующий цикл.
6. Построить и отформатировать график найденной функции в точках интервала.
II Найти решение обычного дифференциального уравнения с использованием встроенной функции rkfixed.
1. Задать начальные значения переменной, которая есть в уравнении.
2. Записать уравнения, используя знак логического равенства между правой и левой частями уравнения с панели управления Evaluation (Выражения).
3. Задать количество шагов интегрирования уравнения на интервале.
4. Присвоить функции, относительно которой решается уравнение, значение rkfixed с параметрами: функция, интервал интегрирования, количество шагов на интервале интегрирования, оператор дифференциального уравнения.
5. Определить значение найденной функции в точках интервала, для чего создать соответствующий цикл.
6. Построить и отформатировать график найденной функции в точках интервала.
Таблица 8.1 – Варианты задания к лабораторной работе №8
| Номер варианта | Уравнение f(x,y) | Начальные условия | Интервал нахождения решения | Шаг изменения |
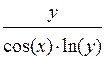
| y(1)=1 | [1,10] | ||
| tg(x)t(y) | y(0)=0 | [0,5] | 0.5 | |
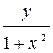
| y(1)=1 | [1,7] | ||
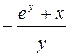
| y(1)=1 | [1, 5] | 0.25 | |
| cos(x-2y)-cos(x+2y) | y(0)=p/4 | [0,4p] | p/2 | |
| 2e-xcos(x)-y | y(0)=0 | [0;3,5] | 0,1 | |
| e-2ycos(x)-y | y(0)=0 | [0;1] | 0,05 | |
| lnôx+2,5xsin(x)ô | y(0)=2,5 | [1;3,5] | 0,2 | |
| e35ysin(x)+y | y(0)=0 | [0;1,5] | 0,1 | |
| x2ln(x+y2) | y(0)=3,5 | [1,2;2,4] | 0,08 | |
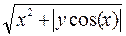
| y(0)=3,6 | [4,1;6,7] | 0,1 | |
| sin(x)+cos(y2) | y(0)=2,2 | [0,8;3,2] | 0,1 | |
| e-2xsin(x+y) | y(0)=16,2 | [4,8;6,4] | 0,1 | |
| 0,7y+x×ln(x+y) | y(0)=2,5 | [12,4;14,1] | 0,08 |
| 0,5x+ye(x-y) | y(0)=3,1 | [8,5;9,7  ]
| 0,05 | |
| x2+ycos(x) | y(0)=1,4 | [0;2,3] | 0,1 | |
| y2-exy | y(0)=1,7 | [2,4;3,5] | 0,05 | |
| xy-e(x-y) | y(0)=2,8 | [1,6;3,1] | 0,1 | |
| sin(xy)-e2x | y(0)=5,7 | [14,5;16,3] | 0,05 | |
| y(0)=1,6 | [5,2;6,8] | 0,1 | |
| y/ln(y) | y(2)=1 | [2;5] | 0,25 | |
| e(x+y)-e(x-y) | y(0)=0 | [0;2.5] | 0,1 | |
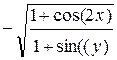
| y(p/4)=0 | [p/4, 3p] | p/8 | |
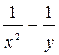
| y(1)=0 | [1;4] | 0.3 | |
| sin(3x)-y×tg(3x) | y(0)=1/3 | [0,4] | 0,25 | |
| cos(x-4y)-cos(x+4y) | y(0)=p/4 | [0,4p] | p/2 | |
| 2e-xcos(x)y | y(0)=0 | [0;3,5] | 0,1 | |
| e-2ycos(x)+y | y(0)=0 | [0;1] | 0,05 | |
| lnôx+sin(x)ô | y(0)=2,5 | [1,5;3,5] | 0,2 | |
| ey+2sin(x) | y(0)=0 | [0;1,5] | 0,1 |
Пример
I Найти решение обычного дифференциального уравнения 
на интервале [0,100]. Функция имеет такие начальные условия: у(0)=1.
1 Ввести ключевое слово Given.
2 Записать, используя логический знак равенства, следующее выражение:
.
3 Начальное условие записать следующим образом, используя логический знак равенства:
у(0)=1.
4 Вычислить числовое решение задачи через использование функции Odesolve:
у:=Odesolve(t,100).
5 Создать цикл t:=0,..10для определения точек интервала
t:=0,..10.
6 Построить график функции в точках интервала и отформатировать его.
|
|
|
|
|
|
|
|
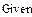
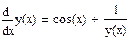
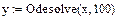
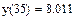
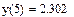
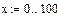
Рисунок 26- График функции
II Найти для вышеприведенной задачи решение с использованием встроенной функции rkfixed.
1. Задать начальное условие
у(0):=0.1.
2. Создать функцию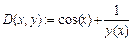 
.
3. Указать количество шагов интегрирования К:=100.
4. Вычислить числовое решение задачи с использованием функции rkfixed. Знак равенства выбирается на панели Логика (Логические).
у=rkfixed(у, х1,х2,К, D).
5. Создать цикл х:=0,..100 для определения точек интервала
х:=0,..100.
6. Построить график функции в точках интервала и отформатировать его.
|
|
 .
|
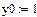
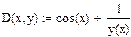
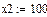
Примечание: результаты решения дифференциального уравнения двумя подходами должны совпадать. Можно также использовать для решения дифференциального уравнения следующие встроенные функции: Bulstoer, Rkadapt. Они имеют такие же параметры как и функция rkfixed, но результаты выдают с разной точностью:
,
.
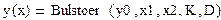Контрольные вопросы
1. Какие встроенные функции позволяют найти решение обычных дифференциальных уравнений?
2. Нужно ли обязательно задавать начальные условия для решения обычных дифференциальных уравнений?
3. Как влияет на результат количество точек разбивки интервала интегрирования обычных дифференциальных уравнений?
Лабораторная работа № 9
Интерполяция экспериментальных данных в MathCad
Цель работы: построить с помощью средств MathCad график функции, которая наилучшим образом отображает экспериментальную зависимость и которая представлена данными, которые приведены в таблице.
Указания к выполнению лабораторной работы:
1. Набрать таблицу, которая соответствует варианту.
2. Осуществить линейную интерполяцию, для чего необходимо выполнить следующие действия:
2.1. Ввести векторы данных х и у.
2.2. Определить функцию linterp (х,у, t).
2.3. Вычислить значения этой функции в точках, которые выбрать самостоятельно.
3. Построить график функции.
4. Осуществить сплайн-интерполяцию, используя функцию interp (s,х,у, t), для чего необходимо выполнить следующие действия:
4.1. Ввести векторы данных х и у.
4.2. Ввести функцию cspline (х,у), которая определяет первый аргумент функции interp (s,х,у, t), как векторную величину значений коэффициентов кубического сплайна.
4.3. Определить функцию interp (s,х,у, t).
4.4. Вычислить значения этой функции в точках, которые задать такими же, как и для линейной интерполяции.
5. Построить график функции.
6. Выполнить сравнительный анализ полученных разными подходами интерполяционных графиков и значений функции в одинаковых точках.
Таблица 9.1 – Варианты задания к лабораторной работе № 9
| Номер варианта | Аргументы и значения | Данные | |||||||||||
| х | |||||||||||||
| у | 35,6 | 38,7 | 39,4 | 40,8 | 43,3 | 42,9 | 41,8 | ||||||
| х | |||||||||||||
| у | 135,2 | 138,7 | 139,9 | 141,6 | 140,1 | 142,5 | 141,8 | ||||||
| х | |||||||||||||
| у | 9,7 | 10,3 | 10,8 | 10,2 | 11,9 | 11,4 | 11,4 | ||||||
| х | |||||||||||||
| у | 14,5 | 16,2 | 16,5 | 17,2 | 19,8 | 17,7 | 17,5 | ||||||
| х | |||||||||||||
| у | 32,8 | 30,2 | 21,7 | 27,8 | 27,5 | 27,2 | 27,9 | ||||||
| х | |||||||||||||
| у | 36,3 | 38,5 | 39,7 | 39,1 | 39,0 | 38,7 | 40,0 | ||||||
| х | |||||||||||||
| у | 52,7 | 56,5 | 60,7 | 54,8 | 70,4 | 68,1 | 67,8 | ||||||
| х | |||||||||||||
| у | 11,12 | 10,6 | 11,31 | 11,02 | 12,0 | 12,73 | 11,12 | ||||||
| х | |||||||||||||
| У | 1,8 | 2,9 | 2,0 | 3,6 | 3,8 | 3,9 | 4,1 | ||||||
| х | |||||||||||||
| у | 9,8 | 10,1 | 10,3 | 11,9 | 10,9 | 11,8 | 12,1 | ||||||
| х | |||||||||||||
| у | 4,7 | 4,6 | 4,6 | 5,3 | 5,3 | 5,5 | 5,6 | ||||||
| х | |||||||||||||
| у | 2,12 | 1,28 | 1,71 | 1,6 | 1,11 | 1,18 | 1,02 | ||||||
| х | |||||||||||||
| у | 2,46 | 2,38 | 2,79 | 2,63 | 2,86 | 3,46 | 4,32 | ||||||
| х | |||||||||||||
| у | 51,4 | 54,9 | 57,4 | 57,7 | 58,9 | 64,3 | 67,8 | ||||||
| х | |||||||||||||
| у | 17,7 | 19,5 | 19,4 | 20,6 | 20,8 | 22,5 | 23,6 | ||||||
| х | |||||||||||||
| у | 45,0 | 47,3 | 48,8 | 47,1 | 45,4 | 45,8 | 46,1 | ||||||
| х | |||||||||||||
| у | 14,6 | 13,6 | 12,0 | 18,7 | 19,8 | 20,1 | 21,5 | ||||||
Продолжение табл.9.1
| х | |||||||||
| у | 36,1 | 33,6 | 32,9 | 36,9 | 33,2 | 36,9 | 38,3 | ||
| х | |||||||||
| у | 39,4 | 41,8 | 43,3 | 42,9 | 41,8 | 41,4 | 42,6 | ||
| х | |||||||||
| у | 15,6 | 14,0 | 12,7 | 17,8 | 20,1 | 21,5 | 22,8 | ||
| х | |||||||||
| у | 18,87 | 16,0 | 19,32 | 19,6 | 18,02 | 20,88 | 21,55 | ||
| х | |||||||||
| у | 15,6 | 15,3 | 17,7 | 19,9 | 20,0 | 19,7 | 25,5 | ||
| х | |||||||||
| у | 24,8 | 27,2 | 22,2 | 30,4 | 35,6 | 38,7 | 39,4 | ||
| х | |||||||||
| у | 37,7 | 42,8 | 40,5 | 41,3 | 40,2 | 48,9 | 47,1 | ||
| х | |||||||||
| у | 17,8 | 21,6 | 20,9 | 24,8 | 21,2 | 20,2 | 30,2 | ||
| х | |||||||||
| у | 4,5 | 5,1 | 5,5 | 5,0 | 6,1 | 6,0 | 6,1 | ||
| х | |||||||||
| у | 62,0 | 66,1 | 63,6 | 66,3 | 71,2 | 70,8 | 72,5 | ||
| х | |||||||||
| у | 24,8 | 27,3 | 28,4 | 35,0 | 39,1 | 40,5 | 37,3 | ||
| х | |||||||||
| у | 3,1 | 3,5 | 3,7 | 3,8 | 4,9 | 4,1 | 4,3 | ||
Пример
Построить график экспериментально заданной функции
| х | |||||||
| у | 4,1 | 2,4 | 4,3 | 3,6 | 5,2 | 5,9 |
и определить ее значения для х=2.4 и х=7.
1. Создать векторы для переменных х и у.
 ,
|
.
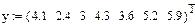2. Определить функцию линейной интерполяции linterp(x,y,t).
.
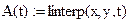3. Построить график функции.
Рисунок 27- График функции линейной интерполяции
4. Вычислить значения функции в точках х=2.4 и х=7.
5. Определить функцию сплайн-интерполяции interp (s,х,у, t), для чего необходимо выполнить следующие действия:
5.1. Ввести векторы данных х и у.
5.2. Ввести функцию cspline (х,у), которая определяет первый аргумент функции interp (s,х,у, t).
| ,
|
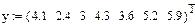
Рисунок 28- График функции сплайн-интерполяции
6. Провести сравнительный анализ результатов, которые получены при разных типах интерполяции.
Контрольные вопросы
1. Опишите особенности применения линейной интерполяции.
2. Опишите особенности применения сплайн-интерполяции.
Лабораторная работа № 10.
Анализ и синтез сигналов с помощью преобразования Фурье
Цель работы: Научиться находить спектральные характеристики сигналов.
