Известно, что экспериментальные данные, как правило, задаются дискретно в виде массива данных из двух пар чисел (хі, уі). В связи с этим возникает задача аппроксимации дискретных данных непрерывной функцией f(x). В MathCad для обработки экспериментальных данных существуют встроенные функции, которые позволяют выполнять интерполяцию.
Для построения линейной интерполяции служит встроенная функция linterp
linterp(x,y, t) – функция, которая аппроксимирует данные векторов х и у кусочно-линейной зависимостью;
– х – вектор действительных данных аргумента;
– у – вектор действительных данных значений того же размера;
– t – значение аргумента, при котором вычисляется интерполяционная функция.
Замечание: элементы вектора х должны быть определены в порядку возрастания.
Чтобы осуществить линейную интерполяцию, надо выполнить следующие действия:
1. Ввести векторы данных х и у.
2. Определить функцию lіnterp (х, в, t).
3. Вычислить значение этой функции в необходимых точках, например, lіnterp(x,y,2.4) = 3.52 или lіnterp(х,в,6) =5.9, или построить ее график.
Замечание: функция A (t) на графику имеет аргумент t, а не х. Это означает, что функция A (t) исчисляется не только при заданных значениях аргумента, а в намного большем количестве аргументов в интервале изменения переменной, что автоматически обеспечивает Mathсad. Mathсad, по умолчанию, соединяет точки графика прямыми линиями, осуществляет их линейную интерполяцию.
В большинстве практических приложений желательно соединить экспериментальные точки не ломанной линией, а гладкой кривой. Лучше всего для этих целей подходит интерполяция кубическими сплайнами, т.е. отрезками кубических парабол.
іnterp(s,x,y,t) - функция, которая аппроксимирует данные векторов х и у кубическими сплайнами;
– s - вектор вторых производных, созданный одной из функций csplіne, psplіne или lsplіne;
– х - вектор действительных данных аргумента, элементы которого расположены в порядке возрастания;
– y - вектор действительных значений того же размера;
– t - значение аргумента, при котором исчисляется функция, которая интерполируется.
Перед применением функции іnterp необходимо предварительно определить первый из ее аргументов - векторную переменную s. Выполняется это с помощью одной из трех встроенных функций тех же аргументов (х,у).
– іspііne(x,y) - вектор значений коэффициентов линейного сплайна;
– pspііne(x,y) - вектор значений коэффициентов квадратичного сплайна;
– csplіne(x,y) - вектор значений коэффициентов кубического сплайна;
– х, y - векторы данных.
Более сложный тип интерполяции - так называемая интерполяция В-сплайнами. В отличие от обычной сплайн-интерполяции, сшивание элементарных В-сплайнов выполняется не в точках х и у, а в других точках, координаты которых предлагается ввести пользователю. Сплайны могут быть полиномами 1, 2 или 3 степени (линейные, квадратичные или кубические). Применяется интерполяция В-сплайнами точно так же, как и обычная сплайн-интерполяция, разница состоит только в определении вспомогательной функции коэффициентов сплайна.
Лабораторная работа №1
Нахождение корней уравнения в MathCad
Цель работы: нахождение корней уравнения в программе MathCad с использованием встроенных функций root, polyroots, символьного решения.
Указания к выполнению лабораторной работы:
I Нахождение корней уравнения в программе MathCad с использованием встроенной функции root
1. Запустить программу MathCad.
2. Записать на рабочем листе MathCad вид функции f(х), для которой необходимо найти на заданном интервале корни.
3. Создать цикл из точек интервала, на котором определяются корни, и вычислить в этих точках функцию f(х). Построить график функции f(х) и график функции х0=0 (т.е. ось х).
4. Определить точки пересечения двух кривых f(х) и х0, которые будут приближением к корням уравнения.
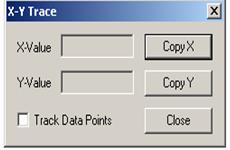
4.1. Использовать для определения на графике значений корней в контекстном меню (рис.17, a) опцию Trace (рис. 17,б), установить флажок в окне Track Data Poіnt.
4.2. Подвести курсор мыши к точкам пересечения кривых, координаты точек пересечения кривых, т.е. корни, будут представлены в окнах Х-Value и У- Value, а на графике отобразится вертикальная прямая.
5. Задать для независимой переменной х начальное приближение, которое выбирается как значение точки пересечения кривых f(х) и х0. Обратиться ко встроенной в MathCad функции root(f(x), x) (функция root возвращает значение независимой переменной х, для которой f(х) равняется 0) и найти корень х1.
6. Найти второй (х2) и третий (х3) корни уравнения f(х)=0 (уравнение третьей степени имеет не больше трех действительных корней), задав для них соответственно их начальные значения как координаты точек пересечения кривых f(х) и х0 и использовав функцию root.

а) б)
Рисунок 17 – Диалоговые окна для определения координат точек пересечения кривых
ІІ Нахождение корней уравнения в программе MathCad с использованием встроенной функции polyroots, которая возвращает вектор, имеющий все корни уравнения, коэффициенты уравнения при этом задаются вектором.
1. Записать на рабочем листе MathCad вид функции f(х), для которой необходимо найти на заданном интервале корни.
2. Записать как вектор v все коэффициенты уравнения, расположить их в порядке увеличения степеней.
3. Найти корни, обратившись ко встроенной функции r:=polyroots(v), результат будет получено относительно трансформированного вектора rT.
4. Для интервала нахождения корня и количества элементов вектора rT создать соответствующие циклы и вычислить значение функции в точках цикла.
5. Построить график функции в точках цикла, а также в найденных точках корней, в которых функция будет иметь значения, равные нулю.
ІІІ Нахождение корней уравнения в программе MathCad с использованием символьных решений уравнений.
1. Ввести левую часть уравнения.
2. Ввести знак равенства с использованием панели управления Evaluatіon (Выражения) или с помощью нажатия клавиш Ctrl + =.
3. За знаком равенства ввести правую часть уравнения.
4. Выделить переменную, относительно которой решается уравнение.
5. Выбрать команду Symbolіc/Varіable/Solve.
По окончанию решения корни уравнения выводятся в виде вектора.
ІV Найти приближенное решение с использованием функции mіnerr(x1,...).
1. Задать приближение последовательно для первого корня х:=1.
2. Ввести ключевое слово gіven (дано), из которого начинается блок решений.
3. Записать уравнение, используя знак логического равенства между правой и левой частями уравнения.
4. Обратиться к функции mіnerr(x). Корень будет найдено.
Таблица 1.1 – Варианты заданий к лабораторной работе № 1
| № варианта | Интервал нахождения корней | Уравнение |
| [-1; 3] | x3-2,92x2+1,4355x+0,791=0 | |
| [-2; 3] | x3-2,56x2-1,325x+4,395=0 | |
| [-3,5; 2,5] | x3+2,84x2-5,606x-14,766=0 | |
| [-2,5; 2,5] | x3+1,41x2-5,472x-7,38=0 |
Продолжение табл.1.1
| [-1,6; 1,1] | x3+0,85x2-0,432x+0,044=0 | ||
| [-1,6; 1,6] | x3-0,12x2-1,478x+0,192=0 | ||
| [-1,6; 0,8] | x3+0,77x2-0,251x-0,017=0 | ||
| [-1,4; 1] | x3+0,88x2-0,3999x-0,0376=0 | ||
| [-1,4; 2,5] | x3+0,78x2-0,827x-0,1467=0 | ||
| [-2,6; 1,4] | x3+2,28x2-1,9347x-3,90757=0 | ||
| [-2,6; 3,2] | x3-0,805x2-7x+2,77=0 | ||
| [-3; 3] | x3-0,345x2-5,569x+3,15=0 | ||
| [-2; 3,4] | x3-3,335x2-1,679x+8,05=0 | ||
| [-1; 2,8] | x3-2,5x2+0,0099x+0,517=0 | ||
| [-1,2; 3] | x3-3x2+0,569x+1,599=0 | ||
| [-2,5; 2,5] | x3-2,2x2+0,82x+0,23=0 | ||
| [-1,2; 4,6] | x3-5x2+0,903x+6,77=0 | ||
| [-1; 7,4] | x3-7,5x2+0,499x+4,12=0 | ||
| [-1.6; 9] | x3-7,8x2+0,899x+8,1=0 | ||
| [-3,4; 2] | x3+2x2-4,9x-3,22=0 | ||
| [-3,4; 1,2] | x3+3x2-0,939x-1,801=0 | ||
| [-4,6; 3,0] | x3+5,3x2+0,6799x-13,17=0 | ||
| [-2,4; 8,2] | x3-6,2x2-12,999x+11,1=0 | ||
| [-3,2; 2,7] | x3-0,34x2-4,339x-0,09=0 | ||
| [-1; 3] | x3-1,5x2+0,129x+0,07=0 | ||
| [-1; 3] | x3-5,5x2+2,79x+0,11=0 | ||
| [-1; 3] | x3-5,7x2-6,219x-2,03=0 | ||
| [-1; 3] | x3-3,78x2-7,459x-4,13=0 | ||
| [-1; 3] | x3-5x2-9,9119x+0,01=0 | ||
| [-1; 3] | x3-7x2-1,339x-7,55=0 |
Пример
І Для уравнения  найти корни на интервале [-1, 1], шаг изменения переменной х равен 0.1.
найти корни на интервале [-1, 1], шаг изменения переменной х равен 0.1.
1 Записать цикл из точек интервала х:=-1, -0.9..1.
2 Записать функции 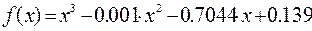 и х0 =0.
и х0 =0.
3 Построить графики для этих функций.
4 Определить на графике точки пересечения кривых 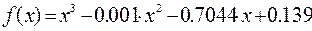 и х0 =0.
и х0 =0.
5 Задать как приближение значения точек пересечения х1, х2, х3. В примере х1=-0.9, х2=0.2, х3= 0.7.
6 Вычислить значение корней с помощью формул: root (f(x1),x1), root (f(x2),x2), root (f(x3),x3). Полученные значения корней такие: х1=-0.92, х2=0.21, х3= 0.721 (рис. 18).

Рисунок 18 – Результат нахождения корней с использованием функции root
II Для уравнения  найти корни на интервале [-1.1, 7.1], шаг изменения переменной х равен 0.1.
найти корни на интервале [-1.1, 7.1], шаг изменения переменной х равен 0.1.
1. Создать вектор из коэффициентов уравнения, используя панель управления Matrix (Матрица) (рис.19) и задав один столбец и четыре строки для коэффициентов уравнения.
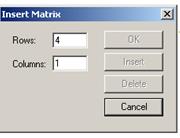
Рисунок 19 – Диалоговое окно для определения вектора из коэффициентов уравнения
Вектор из коэффициентов уравнения будет иметь следующий вид
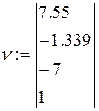
2. С помощью встроенной функции r:= polyroots (v) найти корни уравнения и представить их в виде вектора rT, транспонированного по отношению к r, то есть преобразованного из столбца в строку.
3. Создать циклы для переменной х и количества найденных корней:

4. Построить графики для функции и определить функцию в точках корней. В точках корней значения функции равны нулю.
5. Определить значения корней на графике (рис. 20).
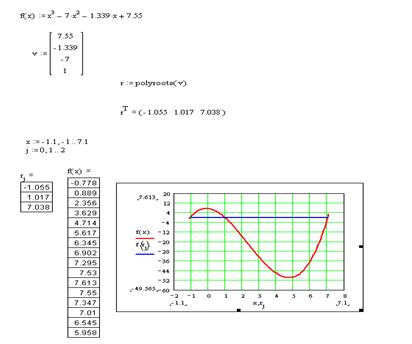
Рисунок 20 – Результат нахождения корней с использованием функции polyroots
III Для уравнения  найти корни с использованием символьных решений уравнений.
найти корни с использованием символьных решений уравнений.
1. Записать левую часть уравнения
 .
.
2. Поставить логический знак «=» и в правой части записать 0.
3. Выделить переменную х.
4. Обратиться в главном меню MathCad к команде Symbolic/Variable/ Solve.
Найдены корни уравнения запишутся в виде вектора:

IV Найти приближенное решение вышеприведенного уравнения с использованием функции minerr (x 1,…).
1. Задать приближение последовательно для первого корня х:=1.
2. Ввести ключевое слово given (дано), с которого начинается блок решений.
3. Записать уравнение, используя знак логического равенства между правой и левой частью уравнения.
4. Обратиться к функции minerr (x). Корень будет найдено.
5. Аналогические действия выполнить для двух других корней уравнения, поскольку уравнения третьей степени имеет не больше трех корней.

Контрольные вопросы
1 Какие встроенные функции позволяют находить корни уравнения?
2 Как выполняется символьное нахождение корней уравнений?
Лабораторная работа №2
Действия с матрицами в MathCad
Цель работы: выполнение действий с матрицами в программе MathCad.
Указания к выполнению лабораторной работы:
1. Запустить программу MathCad.
2. Создать матрицы  ,
,  ,
,  ,
,  ,
,  ,
,  из коэффициентов a, b, c, m, k, n в соответствии с вариантом задания.
из коэффициентов a, b, c, m, k, n в соответствии с вариантом задания.
3. Выполнить действия с матрицами в соответствии с вариантом задания.
4. Найти ранг матрицы А.
5. В символьном виде выполнить транспонирование матрицы В, инвертирование матрицы А.
6. Найти обратную матрицу К. Найти детерминант матрицы А.
Таблица 2.1 – Варианты заданий к лабораторной работе № 2
| Номер варианта | Значение элементов матриц | Действия с матрицами |
| a=1; b=0.5; c=-1; m=2; k=-2.1;n=-0.8 | 1) A+A×M; 2) B×C; 3) M3; 4)D+m×K; 5)A×D+D×M; 6)K-2 | |
| a=-2; b=1; c=1.5; m=-3; k=-0.1;n=1.8 | 1) A+B×M; 2) M×C; 3) B3; 4)C+m×K; 5)AB+D×K 6)D-3 | |
| a=-1; b=5; c=1.3; m=0.9; k=0.1;n=-0.5 | 1) A-M; 2) B-a×C 3) M2-B; 4)D-×K; 5)A+7×D; 6)A-2 | |
| a=1; b=0.5; c=1; m=0.2; k=0.27;n=0.7 | 1) A2; 2) B×C+M; 3) n×M2; 4)D-K; 5)A×B-D×C; 6)D-2 | |
| a=3; b=2.1; c=0.91; m=1.2; k=1; n=3 | 1) A2+M; 2) B-M; 3) b×C-3; 4)D+3K; 5)A×K-D; 6)M-2 | |
| a=4; b=-0.5; c=-1; m=3.2; k=1.1;n=1.8 | 1) A+B×M; 2) M×C; 3) B3; 4)C+m×K; 5)AB+D×K 6)D-3 | |
| a=1; b=2.5; c=0.3; m=1; k=-2.1;n=-0.8 | 1) A-M; 2) B-a×C 3) M2-B; 4)D-×K; 5)A+7×D; 6)A-2 | |
| a=2; b=0.5; c=-1.1; m=2; k=1.9;n=-3.8 | 1) A2; 2) B×C+M; 3) n×M2; 4)D-K; 5)A×B-D×C; 6)D-2 | |
| a=3; b=-2.5; c=4; m=3; k=-2.1;n=0.8 | 1) A2+M; 2) B-M; 3) b×C-3; 4)D+3K; 5)A×K-D; 6)M-2 | |
| a=3.1; b=1.5; c=2.1; m=3.2; k=1.1;n=-1.6 | 1) A+A×M; 2) B×C; 3) M3; 4)D+m×K; 5)A×D+D×M; 6)K-2 | |
| a=-2; b=1; c=1.5; m=-3; k=-0.1;n=1.8 | 1) A+B×M; 2) M×C; 3) B3; 4)C+m×K; 5)AB+D×K 6)D-3 | |
| a=-1; b=5; c=1.3; m=0.9; k=0.1;n=-0.5 | 1) A-M; 2) B-a×C 3) M2-B; 4)D-×K; 5)A+7×D; 6)A-2 | |
| a=1; b=0.5; c=1; m=0.2; k=0.27;n=0.7 | 1) A2; 2) B×C+M; 3) n×M2; 4)D-K; 5)A×B-D×C; 6)D-2 | |
| a=3; b=2.1; c=0.91; m=1.2; k=1; n=3 | 1) A2+M; 2) B-M; 3) b×C-3; 4)D+3K; 5)A×K-D; 6)M-2 | |
| a=4; b=-0.5; c=-1; m=3.2; k=1.1;n=1.8 | 1) A+B×M; 2) M×C; 3) B3; 4)C+m×K; 5)AB+D×K 6)D-3 | |
| a=1; b=2.5; c=0.3; m=1; k=-2.1;n=-0.8 | 1) A+B×M; 2) M×C; 3) B3; 4)C+m×K; 5)AB+D×K 6)D-3 |
Продолжение табл. 2.1
| a=2; b=0.5; c=-1.1; m=2; k=1.9;n=-3.8 | 1) A-M; 2) B-a×C 3) M2-B; 4)D-×K; 5)A+7×D; 6)A-2 | |
| a=3; b=-2.5; c=4; m=3; k=-2.1;n=0.8 | 1) A2; 2) B×C+M; 3) n×M2; 4)D-K; 5)A×B-D×C; 6)D-2 | |
| a=3.1; b=1.5; c=2.1; m=3.2; k=1.1;n=-1.6 | 1) A2+M; 2) B-M; 3) b×C-3; 4)D+3K; 5)A×K-D; 6)M-2 | |
| a=1; b=0.5; c=-1; m=2; k=-2.1;n=-0.8 | 1) A+A×M; 2) B×C; 3) M3; 4)D+m×K; 5)A×D+D×M; 6)K-2 | |
| a=-2; b=1; c=1.5; m=-3; k=-0.1;n=1.8 | 1) A+B×M; 2) M×C; 3) B3; 4)C+m×K; 5)AB+D×K 6)D-3 | |
| a=-1; b=5; c=1.3; m=0.9; k=0.1;n=-0.5 | 1) A-M; 2) B-a×C 3) M2-B; 4)D-×K; 5)A+7×D; 6)A-2 | |
| a=1; b=0.5; c=1; m=0.2; k=0.27;n=0.7 | 1) A2; 2) B×C+M; 3) n×M2; 4)D-K; 5)A×B-D×C; 6)D-2 | |
| a=3; b=2.1; c=0.91; m=1.2; k=1; n=3 | 1) A2+M; 2) B-M; 3) b×C-3; 4)D+3K; 5)A×K-D; 6)M-2 | |
| a=4; b=-0.5; c=-1; m=3.2; k=1.1;n=1.8 | 1) A+B×M; 2) M×C; 3) B3; 4)C+m×K; 5)AB+D×K 6)D-3 | |
| a=1; b=2.5; c=0.3; m=1; k=-2.1;n=-0.8 | 1) A+A×M; 2) B×C; 3) M3; 4)D+m×K; 5)A×D+D×M; 6)K-2 | |
| a=2; b=0.5; c=-1.1; m=2; k=1.9;n=-3.8 | 1) A+B×M; 2) M×C; 3) B3; 4)C+m×K; 5)AB+D×K 6)D-3 | |
| a=3; b=-2.5; c=4; m=3; k=-2.1;n=0.8 | 1) A-M; 2) B-a×C 3) M2-B; 4)D-×K; 5)A+7×D; 6)A-2 | |
| a=3.1; b=1.5; c=2.1; m=3.2; k=1.1;n=-1.6 | 1) A2; 2) B×C+M; 3) n×M2; 4)D-K; 5)A×B-D×C; 6)D-2 | |
| a=-2; b=1; c=1.5; m=-3; k=-0.1;n=1.8 | 1) A2+M; 2) B-M; 3) b×C-3; 4)D+3K; 5)A×K-D; 6)M-2 |
Пример
Выполнить действия с матрицами, создав их из заданных коэффициентов a=1, b=2, c= 3, m=4, k=5, n=6. Матрицы имеют следующий вид:

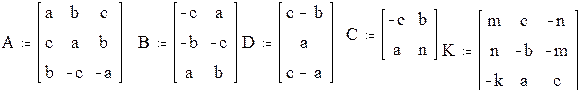
1. Создать матрицы.
1.1. Выбрать панель управления Matrіx (Матрица).
1.2. Определить число строк и столбцов для каждой матрицы (рис.21).

Рисунок 21 - Диалоговое окно для определения размера матрицы
1.3. Матрицы в примере имеют такие размеры: А - (3´3), В - (3´2), С(2´2), М(1´2), К(3´3).
1.4. Заполнить матрицы соответствующими параметрами (рис. 29).
2 Выполнить следующие действия с матрицами:
1) А+n·K; 2)A·B; 3) A2; 4) A·D; 5)D·M; 6) D-1.
3 Найти ранг матрицы А (ранг матрицы -наибольший порядок минора этой матрицы, который отличный от нуля): rank(A).
4 В символьном виде выполнить транспонирование матрицы В, т.е. заменить местами строки и столбцы матрицы В.
4.1 Выделить матрицу В.
4.2 Обратиться в главном меню к команде Symbolіc / Matrіx/Transpose (рис. 28).
5 В символьном виде выполнить инвертирование матрицы А (т.е. найти матрицу, которая будет обратной к матрице А).
5.1 Выделить матрицу A.
5.2 Обратиться в главном меню к команде Symbolіc/Matrіx/Іnvert (рис.28).
6 В символьном виде найти обратную матрицу К.
6.1 Выделить матрицу К.
6.2 Обратиться в главном меню к команде Symbolіc / Matrіx/Іnvert (рис.28).
7 В символьном виде найти детерминант (определитель) матрицы А.
7.1 Выделить матрицу A.
7.2 Обратиться в главном меню к команде Symbolіc/Matrіx/Determіnant (рис.22).

Рисунок 22 – Меню Symbolic для работы с матрицами в символьном виде

Рисунок 23 – Результаты вычисления матриц
Контрольные вопросы
1 Як можно создать матрицу и вектор?
2 Какие действия выполняются с матрицами?
3 Как определяются элементы матрицы?
Лабораторная работа №3
Нахождение решений системы линейных уравнений в MathCad
Цель работы: нахождение решений системы линейных уравнений в программе MathCad.
Указания к выполнению лабораторной работы:
I Найти решение системы линейных уравнений с использованием функции soln.
1 Запустить программу MathCad.
2 Создать матрицу А из коэффициентов при неизвестных.
3 Создать вектор b из свободных членов.
4 Обратиться к встроенной программе решения линейных уравнений soln и записать soln1:=А-1 ×b.
5 Получить решение линейного уравнения у векторному виде
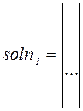 .
.
II Найти решение системы линейных уравнений с использованием так званого «блоку решений».
1 Задать начальные значения переменным, которые есть в уравнении.
2 Ввести ключевое слово given (дано), с которого начинается блок решений.
3 Записать уравнение, используя знак логического равенства между правой и левой частью уравнения из панели управления Evaluation (Выражения).
4 Ввести ключевое слово find (найти), которым заканчивается блок решений.
III Найти решение вышеприведенной системы уравнений с использованием функции lsolve.
1Создать матрицу А из коэффициентов при неизвестных.
2 Создать вектор b из свободных членов.
4 Обратиться к встроенной программе решения линейных уравнений lsolve и записать lsolve(А,b).
5 Получить результат решения линейного уравнения в векторном виде
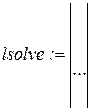 .
.
IV Найти приближенное решение с использованием функции minerr (x 1,…).
1 Задать приближение последовательно для значений переменной х1, х2,… хn.
2 Ввести ключевое слово given (дано), с которого начинается блок решений.
3 Записать систему уравнений, используя знак логического равенства между правой и левой частями каждого уравнения.
4 Обратиться к функции minerr (x 1,x2,..). Значения неизвестных будут найдены.
Таблица 3.1 – Варианты заданий к лабораторной работе № 3
| № варианта | Коэффициенты при неизвестных | Свободные члени | |||
| a11 а21 а31 а41 | а12 а22 а23 а24 | а13 а23 а33 а34 | а14 а24 а34 а44 | в1 в2 в3 в4 | |
Продолжение табл.3.1
| 0,12 | -0,43 | 0,14 | 0,64 | -0,17 | |
| -0,07 | 0,34 | -0,72 | 0,32 | 0,62 | |
| 1,18 | -0,08 | -0,25 | 0,43 | 1,12 | |
| 1,17 | 0,53 | -0,84 | -0,53 | 1,15 | |
| 0,12 | -0,43 | 0,14 | 0,64 | -0,17 | |
| -0,07 | 0,34 | -0,72 | 0,32 | 0,62 | |
| 1,18 | -0,08 | -0,25 | 0,43 | 1,12 | |
| 1,17 | 0,53 | -0,84 | -0,53 | 1,15 | |
| 3,7 | 5,6 | 9,5 | |||
| 3,36 | 31,1 | 1,5 | |||
| 7,93 | 4,2 | 6,3 | 4,4 | ||
| 42,7 | 3,7 | 6,2 | |||
| 1,3 | 1,6 | 2,2 | |||
| 4,4 | 6,7 | 2,5 | |||
| 2,8 | 0,73 | 67,8 | |||
| 3,4 | |||||
| 5,3 | 1,6 | 5,5 | 3,3 | ||
| 4,1 | 6,4 | 3,9 | |||
| 2,1 | 3,3 | 2,04 | 4,9 | ||
| 3,1 | |||||
| 0,2 | |||||
| 8,3 | 5,3 | ||||
| 2,6 | 6,1 | 4,1 | |||
| 0,93 | 3,8 | ||||
| 34,7 | |||||
| 3,6 | |||||
| 3,4 | 4,2 | ||||
| 44,7 |
Продолжение табл.3.1
| 5,1 | 0,2 | ||||
| 3,4 | 5,34 | ||||
| 2,7 | 6,7 | ||||
| 3,3 | |||||
| 2,5 | 1,3 | ||||
| 5,2 | 0,78 | ||||
| 6,11 | 4,2 | ||||
| 6,78 | 3,76 | ||||
| 2,3 | |||||
| 3,4 | 2,5 | ||||
| 0,2 | |||||
| 1,25 | |||||
| 3,3 | 8,2 | ||||
| 1,2 | |||||
| 1,3 | |||||
| 5,9 | |||||
| 6,6 | |||||
| 3,3 | 2,1 | ||||
| 4,8 | |||||
| 0,4 | |||||
| 0,2 | |||||
| 1,3 | 1,5 | 2,22 | 3,2 | ||
| 3,4 | 5,55 | 1,3 | |||
| 3,3 | 2,2 | 6,77 | |||
| 4,9 | 3,6 | 6,88 | |||
| 0,4 | |||||
| 0,3 | |||||
| 3,3 | 7,6 | 5,5 | |||
| 5,4 | |||||
| 9,2 | |||||
| 3,2 | |||||
| 0,44 | |||||
| 0,67 |
Продолжение табл.3.1
| 3,35 | 5,3 | ||||
| 4,22 | 6,7 | 3,5 | |||
| 2,8 | 3,8 | 2,9 | |||
| 2,34 | 3,44 | ||||
| 5,23 | |||||
| 13,4 | 6,33 | 5,1 | 2,11 | 3,33 | |
| 4,66 | 6,1 | 3,33 | 5,44 | 0,11 | |
| 2,22 | 2,55 | 6,33 | 4,44 | ||
| 2,98 | 3,78 | 6,11 | 3,33 |
Пример
I Найти решение системы уравнений с использованием функции soln

1 Создать матрицу А
А:=  .
.
2 Создать вектор b
b:=  .
.
3 Найти решение системы, используя функцию soln
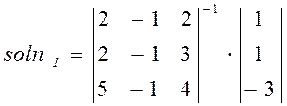 .
.
4 Результат решения

II Найти решение вышеприведенной системы уравнений с использованием так называемого «блока решений»
1 Задать начальные значения переменным, которые присутствуют в уравнении
x=0; y=0; z=0.
2 Ввести ключевое слово given (дано), с которого начинается блок решений.
3 Записать уравнение, используя знак логического равенства между правой и левой частями уравнения из панели управления Evaluation (Выражения).

4 Ввести ключевое слово find (найти), которым заканчивается блок решений.
find(x,y,z) =
5 Результат решения

III Найти решение вышеприведенной системы уравнений с использованием функции lsolve.
1 Создать матрицу А
 .
.
2 Создать вектор b
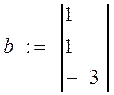 .
.
3 Найти решение системы, используя функцию lsolve:

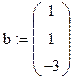

IV Найти решение вышеприведенной системы уравнений с использованием функции minerr (x,у,z).
1 Задать начальные условия для неизвестных, например, x=1,у=1,z=1.
2 Ввести ключевое слово given (дано), с которого начинается блок решений.
3 Записать уравнения, используя знак логического равенства между правой и левой частью уравнения из панели.
4 Обратиться к функции minerr (x,у,z). Решение системы уравнений будет найдено.

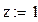



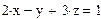


Контрольные вопросы
1 Какие встроенные функции позволяют найти решение системы линейных уравнений?
2 В каком виде представляются результаты решения системы линейных уравнений?
Лабораторная работа №4
Нахождение решений системы нелинейных уравнений в MathCad
Цель работы: нахождение решений системы нелинейных уравнений в программе MathCad.
Указания к выполнению лабораторной работы:
І Найти решение системы нелинейных уравнений с использованием так называемого "блока решений".
1 Задать начальные значения переменным, которые есть в уравнении.
2 Ввести ключевое слово gіven (дано), из которого начинается блок решений.
3 Записать уравнение, используя знак логического равенства между правой и левой частями уравнения из панели управления.
4 Ввести ключевое слово fіnd (найти), которым заканчивается блок решений.
ІІ. Найти приближенное решение с использованием функции mіnerr(x1,...).
1 Задать приближение последовательно для значений переменной х1, х2,... хn.
2 Ввести ключевое слово gіven (дано), из которого начинается блок решений.
3 Записать систему уравнений, используя знак логического равенства между правой и левой частями каждого уравнения.
4 Обратиться к функции mіnerr(x1,x2,..). Значение неизвестных будет найдено.
Таблица 4.1 – Варианты задания к лабораторной работе №4
| № варианта | Система уравнений | № варианта | Система уравнений |
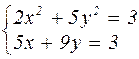
| 
| ||

| 
| ||

| 
| ||

| 
| ||

| 
| ||

| 
| ||

| 
| ||

| 
| ||

| 
| ||

| 
| ||

| 
| ||

| 
| ||

| 
| ||
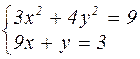
| 
| ||

| 
|
Пример
Найти решение системы нелинейных уравнений с использованием так называемого «блока решений».
1 Задать начальные значения переменным, которые есть в уравнении
x=1; y=1.
2 Ввести ключевое слово given (дано), с которого начинается блок решений.
3 Записать уравнения, используя знак логического равенства между правой и левой частью уравнения из панели управления

4 Ввести ключевое слово find (найти), которым заканчивается блок решений.
find(x,y) =
5 Результат решения

II Найти приближенное решение с использованием функции minerr (x 1,…).
1 Задать приближения последовательно для значений переменной х=1, y=1.
2 Ввести ключевое слово given (дано), с которого начинается блок решений.
3 Записать систему уравнений, используя знак логического равенства между правой и лево частью каждого уравнения.
4 Обратится к функции minerr (x,y.). Значение неизвестных будет найдено.
 
 
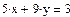  . .
|
Контрольные вопросы
1 Какие встроенные функции позволяют найти решение системы нелинейных уравнений?
2 В каком виде представляются результаты решения системы нелинейных уравнений?
3 Нужно ли задавать начальные приближения при решении системы нелинейных уравнений?
Лабораторная работа № 5
Символьные действия математического анализа в MathCad
Цель работы: определение неопределенных и определенных визначених интегралов и производных в программе MathCad с использованием символьных операций.
Указания к выполнению лабораторной работы:
1 Запустить программу MathCad.
2 Записать на рабочем листе в соответствии с номером варианта формулы для определения неопределенных интегралов, определенных интегралов, производных первого порядка. От производных первого порядка определить производные второго, третьего порядков.
3 Применить последовательно к каждой функции команды меню Symbolic/Simplify, отметив последовательно каждую из функций.
Таблица 5.1 – Варианты задания к лабораторной работе №5
| Номер варианта | Неопределенные интегралы | Определенные интегралы | Производные |

| 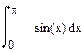
| 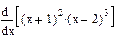
| |

| 
| 
| |

| 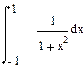
| 
| |

| 
| 
| |
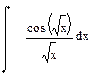
| 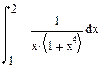
| 
| |

| 
| 
|
Продолжение табл. 5.1

| 
| 
| |

| 
| 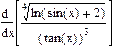
| |
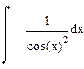
| 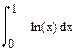
| 
| |

| 
| 
| |
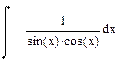
| 
| 
| |

| 
| 
| |

| 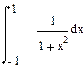
| 
| |

| 
| 
| |

| 
| 
| |

| 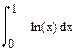
| 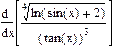
| |

| 
| 
| |
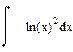
| 
| 
|
Продолжение табл. 5.1

| 
| 
| |

| 
| 
| |
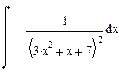
| 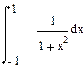
| 
| |

| 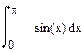
| 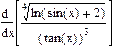
| |

| 
| 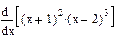
| |

| 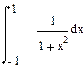
| 
| |

| 
| 
| |

| 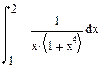
| 
| |

| 
| 
| |

| 
| 
| |

| 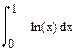
| 
| |
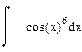
| 
| 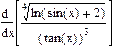
|






