“рением качени€ называетс€ сопротивление, возникающее при качении одного тела по поверхности другого. –ассмотрим круглый цилиндрический каток радиуса r и веса P, наход€щийс€ на шероховатой поверхности
(рис. I.33,а). ѕриложим к оси катка горизонтальную силу 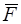 .
.

–ис. I.33
“огда на каток действуют, кроме заданных активных сил 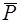 и
и 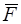 , нормальна€ реакци€
, нормальна€ реакци€  в точке касани€ катка с плоскостью и сила трени€
в точке касани€ катка с плоскостью и сила трени€  , преп€тствующа€ скольжению катка. ак показывает опыт, если сила
, преп€тствующа€ скольжению катка. ак показывает опыт, если сила 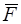 достаточно мала, то каток остаетс€ в покое.
достаточно мала, то каток остаетс€ в покое.
Ќо при такой схеме сил, действующих на цилиндр,  = -
= -  × r отличен от нул€, и при любой сколько угодно малой силе
× r отличен от нул€, и при любой сколько угодно малой силе 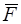 должно было бы начатьс€ качение, что реально не наблюдаетс€.
должно было бы начатьс€ качение, что реально не наблюдаетс€.
ƒл€ объ€снени€ полученного парадокса приходитс€ оказатьс€ от введенной ранее гипотезы абсолютно твердого тела и прин€ть во внимание, что вблизи точки контакта ј поверхности цилиндра и плоскости деформируютс€, и их касание происходит по некоторой площадке конечной ширины (рис. I.33,б), сдвинутой относительно вертикального диаметра катка в направлении качени€. ѕока каток находитс€ в равновесии, силы 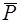 ,
, 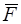 и
и  (равнодействующа€ распределенных по п€тну контакта сил давлени€) уравновешены, т.е. лини€ действи€ силы
(равнодействующа€ распределенных по п€тну контакта сил давлени€) уравновешены, т.е. лини€ действи€ силы  проходит через центр катка, а, значит, ее точка приложени€ ¬ должна быть смещена от вертикали, проход€щей через центр катка, на некоторое рассто€ние d. оэффициент d называетс€ плечом трени€ качени€, ибо он имеет размерность длины. –азложим силу
проходит через центр катка, а, значит, ее точка приложени€ ¬ должна быть смещена от вертикали, проход€щей через центр катка, на некоторое рассто€ние d. оэффициент d называетс€ плечом трени€ качени€, ибо он имеет размерность длины. –азложим силу  на составл€ющие: нормальную
на составл€ющие: нормальную  и касательную
и касательную  Ц силу трени€. —оставим уравнени€ равновеси€ катка: F-T = 0; N Ц P = 0; N × d - T × r = 0.
Ц силу трени€. —оставим уравнени€ равновеси€ катка: F-T = 0; N Ц P = 0; N × d - T × r = 0.
¬ последнем уравнении плечо силы трени€ T ввиду малости деформации вз€то равным r. ѕолученна€ схема действующих сил статически не противоречива. ѕервые два уравнени€ определ€ют трение T = F и нормальную реакцию N = P, а из третьего уравнени€ можно найти рассто€ние d:
d = (F/P) × r. ак видно, с увеличением силы 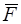 растет рассто€ние d. Ќо величина d определ€ет размеры деформированной области, котора€ не может расти неограниченно, а отсюда следует, что при некотором значении силы F смещение d достигает предельной величины
растет рассто€ние d. Ќо величина d определ€ет размеры деформированной области, котора€ не может расти неограниченно, а отсюда следует, что при некотором значении силы F смещение d достигает предельной величины  и равновесие должно нарушитьс€, каток придет в движение.
и равновесие должно нарушитьс€, каток придет в движение.
—ледовательно, если имеет место равновесие, то выполн€етс€ условие
d £  , которое можно записать и так: момент силы трени€ качени€
, которое можно записать и так: момент силы трени€ качени€
 =
=  £
£ 
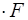 , или
, или  £ (
£ ( /
/  )
)  .
.
«аметим, что дл€ силы, приложенной к катку в точке D (рис. I.33,в) условие равновеси€ имеет вид  £ (
£ ( /
/  )
)  .
.
оэффициент k =  называетс€ коэффициентом трени€ качени€;
называетс€ коэффициентом трени€ качени€;
¬ отличие от коэффициента  коэффициентом трени€ качени€ k €вл€етс€ размерной величиной и имеет размерность длины.
коэффициентом трени€ качени€ k €вл€етс€ размерной величиной и имеет размерность длины.
ѕервые исследовани€ трени€ качени€ были проведены улоном в опытах с качением т€желого цилиндра по плоскости и установлены следующие приближенные законы дл€ максимального момента трени€, преп€тствующего качению:
- максимальный момент в довольно широких пределах не зависит от радиуса катка;
- предельное значение момента ( )max пропорционально нормальному давлению, т.е. нормальной реакции N: (
)max пропорционально нормальному давлению, т.е. нормальной реакции N: ( )max = k × N.
)max = k × N.
|
|
|
оэффициент трени€ качени€ в первом приближении можно полагать не завис€щим от скорости скольжени€ и угловой скорости качени€ катка. Ќо его значение зависит от материала контактирующих тел, состо€ни€ их поверхностей и определ€етс€ опытным путем. ¬ справочниках привод€тс€ значени€ k дл€ различных пар материалов. ќ пор€дке величины k [см], можно судить по его значени€м дл€ некоторых материалов:
- дерево по дереву k=0,05-0,08;
- сталь по стали (колесо по рельсу) k=0,005;
- сталь закаленна€ по стали (шариковый подшипник) k=0,001.
ќбычно k /  <<
<<  дл€ большинства материалов. ќтсюда следует, что трение качени€ весьма мало по сравнению с трением скольжени€ (примерно на два пор€дка). ”же давно было известно, что дл€ перекатывани€ цилиндрического тела требуетс€ гораздо меньша€ сила, чем при его перетаскивании. ѕоэтому в технике, когда это возможно и целесообразно, стрем€тс€ заменить скольжение качением (колесо, катки, шарикоподшипники и т.п.).
дл€ большинства материалов. ќтсюда следует, что трение качени€ весьма мало по сравнению с трением скольжени€ (примерно на два пор€дка). ”же давно было известно, что дл€ перекатывани€ цилиндрического тела требуетс€ гораздо меньша€ сила, чем при его перетаскивании. ѕоэтому в технике, когда это возможно и целесообразно, стрем€тс€ заменить скольжение качением (колесо, катки, шарикоподшипники и т.п.).
ѕример. √руз весом –1 расположен посередине доски, опирающейс€ на два одинаковых цилиндрических катка, которые могут перекатыватьс€ по неподвижной поверхности (рис.I. 34,а). ¬ес каждого катка –2, радиус катка  , коэффициенты трени€ качени€ между катком и доской k1, между катком и основанием Ц k2. Ќайти максимальную силу
, коэффициенты трени€ качени€ между катком и доской k1, между катком и основанием Ц k2. Ќайти максимальную силу 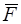 , приложенную горизонтально к доске, при которой доска будет еще оставатьс€ в покое.
, приложенную горизонтально к доске, при которой доска будет еще оставатьс€ в покое.

–ис.I.34
– е ш е н и е. –ассмотрим равновесие одного катка, отбросив мысленно верхнюю и нижнюю поверхности, заменив их действие соответствующими реакци€ми (рис.I. 34,б). —о стороны нижней поверхности на каток действует нормальна€ реакци€ 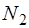 , смещенна€ по отношению к вертикальному диаметру на рассто€ние k2 вправо, т.е. в сторону возможного качени€ катка, и сила трени€
, смещенна€ по отношению к вертикальному диаметру на рассто€ние k2 вправо, т.е. в сторону возможного качени€ катка, и сила трени€  ; со стороны доски Ц нормальна€ реакци€
; со стороны доски Ц нормальна€ реакци€  , смещенна€ на k1 влево от вертикального диаметра, и сила трени€
, смещенна€ на k1 влево от вертикального диаметра, и сила трени€  , равна€ половине силы
, равна€ половине силы 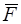 .
.
1.”равнени€ равновеси€ катка в проекции на вертикаль:
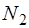 - –2 -
- –2 -  = 0, откуда
= 0, откуда 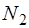 = –2 +
= –2 +  .
.
2. ”равнение равновеси€ катка вместе с грузом:
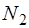 - –2 - –1/2 = 0, откуда
- –2 - –1/2 = 0, откуда 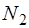 = –2 + –1/2 и, следовательно,
= –2 + –1/2 и, следовательно,  = –1/2.
= –1/2.
3. —умма моментов всех сил относительно точки ј:
 × k1 +
× k1 + 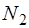 × k2 - (1/2)
× k2 - (1/2)  × 2
× 2  = 0, откуда искома€ максимальна€ сила
= 0, откуда искома€ максимальна€ сила
 .
.
„астные случаи:
1. k1 = k2 = k  =
=  ;
;
2.  =
=  =
=  и –2 << –1
и –2 << –1  =
=  .
.
√Ћј¬ј IV. ќЌ“–ќЋ№Ќјя –јЅќ“ј ѕќ —“ј“» ≈
ѕоскольку основные положени€ и методы теоретической механики широко используютс€ во многих област€х техники, поэтому важной задачей €вл€етс€ применение теоретических результатов к конкретным приложени€м (решение контрольных работ). ѕриведем также краткие рекомендации по решению задач на равновесие тел и примеры выполнени€ контрольных работ.






