Решение уравнений первого порядка

Рассмотрим дифференциальное уравнение первого порядка:

(27.1)

Требуется найти решение на интервале [x₀,x_n], удовлетворяющее начальному условию y(x₀)=y₀.

Для приближённого решения дифференциального уравнения (27.1) интервал [x₀,x_n] разбивается на n частей с шагом h:

x_i+1=x_i+h, i=0,1,2,…,n-1 (27.2)

В полученных точках вычисляются значения y_i.

Метод Эйлера. Согласно методу Эйлера значения y_i определяются по формуле:

y_i+1=y_i+h×f(x_i,y_i) (27.3)

Алгоритм метода Эйлера

1. Ввод n, конечного значения x_n, начального значения x₀ (в переменную x ), ввод y₀ (в переменную y ).

2. Вычисление h= , x=x₀, y=y₀.

3. Вывод x, y.

4. Вычисление y=y+h×f(x,y), x=x+h.

5. Если x>x_n, то переход к 6, иначе – переход к пункту 3.

6. Конец вычислений.

Для получения достоверных результатов значение h должно быть достаточно мало, при этом можно не выводить все получающиеся значения x и y. Целесообразно внести изменения в алгоритм программы так, чтобы вычисления проводились с малым шагом, а вывод результатов − с большим.

Метод Рунге-Кутта. Расчетные формулы метода Рунге-Кутта четвертого порядка имеют вид:

k1=h×f(x_i,y_i)

k2=h×f(x_i+ , y_i+ )

k3=h×f(x_i+ , y_i+ )

k4=h×f(x_i+h, y_i+k3)

y_i+1=y_i+ 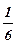×(k1+2×k2+2×k3+k4) (27.4)

x_i+1=x_i+h, i=0,1,2,…, n-1

Для разработки программы, реализующей метод Рунге-Кутта можно использовать тот же алгоритм, что и для метода Эйлера, внеся в него соответствующие изменения.