1. Решить дифференциальные уравнения, представленные в табл. 27.1. В приложении Excel для дифференциального уравнения первого порядка на языке VBA разработать программу решения методом Рунге-Кутта, а для системы дифференциальных уравнений − методом Эйлера.
3. Выполнить вычисления в пакете Mathcad. Результаты сравнить между собой.
Таблица 27.1
| № | Уравнения | Интервал и шаг | Начальные условия |

| [0;1], h=0.05 | y(0)=1 | |
 ; ; 
| [2;4], h=0,1 | z1(2)=3 z2(2)=0 | |

| [1;2], h=0,05 | c(1)=1 | |
 ; ; 
| [0;1], h=0,1 | y1(0)=2 y2(0)=2 | |
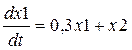 ; ; 
| [1;3], h=0,1 | x1(1)=1 x2(1)=0 | |

| [0;1], h=0,05 | y(0)=4 |
Продолжение таблицы 23.1
| № | Уравнения | Интервал и шаг | Начальные условия |
 ; ; 
| [10;12], h=0,1 | p1(10)=3 p2(10)=0 | |

| [1;2], h=0,05 | y(1)=10 | |

| [0;2], h=0,2 | z(0)=1 | |
 ; ; 
| [1;2], h=0,05 | y1(1)=5 y2(1)=0 | |

| [0;1], h=0,05 | y(0)=8 | |
 ; ; 
| [2;3], h=0,1 | z1(2)=3 z2(2)=1 | |
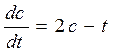
| [1;2], h=0,05 | c(1)=1 | |
 ; ; 
| [0;1], h=0,1 | y1(0)=2 y2(0)=0 | |
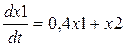 ; ; 
| [2;3], h=0,1 | x1(1)=1 x2(1)=0 | |

| [0;1], h=0,05 | y(0)=9 | |
 ; ; 
| [1;2], h=0,1 | p1(1)=3 p2(1)=1 | |

| [1;2], h=0,05 | y(1)=5 | |

| [0;2], h=0,2 | z(0)=1 | |
 ; ; 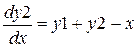
| [1;2], h=0,05 | y1(1)=6 y2(1)=0 |
Продолжение таблицы 23.1
| № | Уравнения | Интервал и шаг | Начальные условия |

| [0;1], h=0,05 | y(0)=1 | |
 ; ; 
| [2;3], h=0,1 | z1(2)=3 z2(2)=0 | |

| [1;2], h=0,05 | c(1)=1 | |

| [0;1], h=0,1 | y1(0)=0 y2(0)=2 | |

| [1;3], h=0,1 | x1(1)=5 x2(1)=0 | |

| [0;1], h=0,05 | y(0)=4 | |
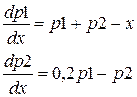
| [0;2], h=0,1 | p1(0)=3 p2(0)=0 | |

| [1;2], h=0,05 | y(1)=6 | |
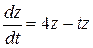
| [0;2], h=0,2 | z(0)=1 | |

| [1;2], h=0,05 | y1(1)=5 y2(1)=1 |






