Равновесный газ с фиксированными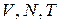 
обменивается энергией с термостатом. Микросостояния газа имеют разные энергии, энергия частицы хаотически меняется с течением времени. Макросостояние не зависит от времени, средняя тепловая энергия частицы газа постоянна, зависит от температуры, от числа степеней свободы частицы и от ее гамильтониана. Если степени свободы частицы входят в гамильтониан симметрично, то на каждую степень свободы приходится одинаковая тепловая энергия, пропорциональная температуре. Теорему предложил Уотерстон в 1845 г., количественное выражение дал Максвелл в 1860 г. и Больцман в 1868 г. Теорема не применима для квантовых систем.
Джон Джеймс Уотерстон (1811–1883)
Джеймс Клерк Максвелл (1831–1879)
Людвиг Больцман (1844–1906)
Используя гамильтониан, найдем средние значения кинетической, потенциальной и полной энергий частицы, обусловленные тепловой энергией.
Гамильтониан частицы характеризует ее микросостояние. Рассмотрим частицу с f степенями свободы и с гамильтонианом, зависящим от модуля проекций импульса и от проекций координаты степенным образом:
, (2.103)
где
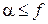– число активизированных степеней свободы с кинетической энергией 
и с импульсами в пределах 
; 
;
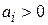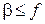– число активизированных степеней свободы с потенциальной энергией 
и с координатами в пределах 
; 
.
Получим средние по фазовому ансамблю значения кинетической, потенциальной и полной энергии частицы при температуре Т.
Средняя энергия частицы складывается из кинетических и потенциальных составляющих вдоль ортогональных осей. Среднюю полную энергию частицы выражаем через статистический интеграл согласно (2.94)
. (2.104)
В статистическом интеграле (2.81)
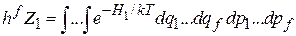
с гамильтонианом (2.103) все интегралы расцепляются, получаем произведение независимых интегралов для каждой активизированной степени свободы
.
Кинетическая и потенциальная составляющие статистического интеграла частицы равны
,
, (2.105)
Используем
,
где 
, 
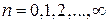, вычисляем интегралы
,
,
где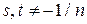 
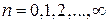, . С учетом
,
из (2.104)
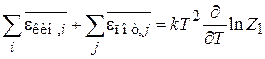
находим
.
Разделяем вклады разных видов энергии и степеней свободы
,
. (2.106)
Для
,
,
учитываем
, 
,
, 
.
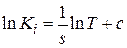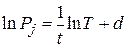Получаем
,
.
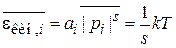Величины 
и 
не зависят от i и j, следовательно, выполняется теорема о равном распределении тепловой энергии по активизированным степеням свободы. С учетом всех степеней свободы находим
,
.
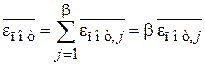В результате средние значения потенциальной, кинетической и полной энергий частицы пропорциональны температуре
,
,
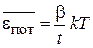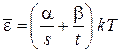. (2.107)
Газ в ограниченном объеме. Если координата ограничена 
, то потенциальная составляющая (2.105)
статистического интеграла частицы равна
.
Результат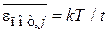 
из (2.107) не применим, выражение 
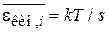можно использовать, если .
Рассмотрим газ в сосуде размером A по оси j, вдоль которой действует однородное потенциальное поле
,
например, электрическое или гравитационное. Тогда верхний предел интеграла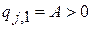 
, и получаем
.
Из (2.106)
находим среднюю потенциальную энергию частицы при температуре Т
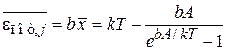. (2.108)
Тепловое движение разбрасывает частицы газа равномерно по всему объему. Этому противостоит внешнее поле, действующее с силой
,
направленной при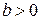 
в сторону уменьшения координаты x.
При низкой температуре силовое действие преобладает над тепловой энергией 
, тогда из (2.108) получаем
. (2.109)
Следовательно, 
и частицы благодаря действию силы оказываются около стенки сосуда при 
. Стенку при 
можно считать расположенной на бесконечности и результат совпадает с (2.107)
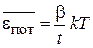
при 
.
С увеличением температуры тепловое движение растет и средняя координата увеличивается. При высокой температуре 
используем разложение 
, и из (2.108)
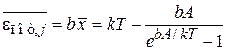
находим
, (2.110)
тогда
.
При 
тепловое движение преобладает над силовым полем и разбрасывает частицы с равной вероятностью по всему объему, среднее положение частицы совпадает с серединой сосуда.
