Элемент объема фазового пространства в распределениях (2.76) и (2.77) выражаем через энергетическую плотность состояний, используя
.
В (2.76)
и (2.77)
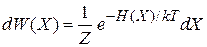
гамильтониан системы 
заменяем на энергию Е. Для газа с температурой Т получаем вероятность обнаружения микросостояний с энергией в интервале 
. (2.87)
Нормировка вероятности
дает статистический интеграл газа
. (2.88)
Для макроскопической системы относительная дисперсия энергии обратно пропорциональна числу частиц согласно (П.1.2). Тогда функция распределения по энергии
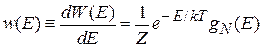
имеет резкий максимум при некотором значении энергии и результаты канонического и микроканонического распределений совпадают.
Каноническое распределение частицы по энергии. Выделяем в газе частицу и рассматриваем остальные как термостат. В (2.87) и (2.88) полагаем 
, 
и получаем
, (2.89)
где 
– вероятность обнаружения частицы с энергией в интервале 
; 
– число частиц с энергией в интервале ; N – полное число частиц газа;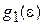 
– энергетическая плотность состояний частицы.
Согласно (2.88) статистический интеграл частицы связан с ее энергетической плотностью состояний преобразованием Лапласа
. (2.90)
В частности для степенной зависимости 
находим
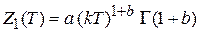. (2.91а)
