Молекула массой m состоит из двух одинаковых атомов, находящихся на расстоянии 2 r и вращающихся вокруг центра масс. Найдем статистический интеграл вращений при температуре Т.
При вращении изменяется угловое положение атомов. Используем сферические координаты с центром в точке симметрии молекулы. На рисунке черный круг – атом, второй атом в симметричной точке не показан.

При вращении изменяются углы φ и θ, молекула движется по окружностям с радиусами, соответственно, 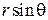 и r. Линейные скорости выражаем через угловые скорости и радиусы окружностей
и r. Линейные скорости выражаем через угловые скорости и радиусы окружностей
 – вдоль
– вдоль  ,
,
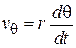 – вдоль
– вдоль  .
.
Обобщенными координатами фазового пространства являются углы φ и θ. Для нахождения обобщенных импульсов, соответствующих этим координатам, используем уравнение Лагранжа, связывающее импульс со скоростью:
 .
.

Жозеф Луи Лагранж (1736–1865)
Функция Лагранжа

зависит от координат и скоростей. При отсутствии потенциальной энергии функция Лагранжа равна кинетической энергией. Для двухатомной молекулы с моментом инерции 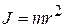 относительно прямой, перпендикулярной к оси молекулы и проходящей через центр масс, получаем
относительно прямой, перпендикулярной к оси молекулы и проходящей через центр масс, получаем
 .
.
Откуда обобщенные импульсы
 ,
,
 .
.
Угловые скорости выражаем через импульсы
 ,
,
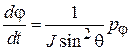 .
.
Результаты подставляем в
 ,
,
и находим гамильтониан
 .
.
Статистический интеграл частицы (2.17)
 ,
,
где
 ,
,
получает вид
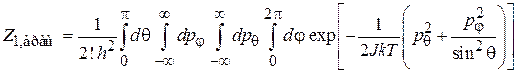 .
.
Интегрируем вначале по j, затем по p q, p j и в конце по θ. Интегралы по p q и по p j сводятся к интегралу Пуассона
 ,
,
находим
 ,
,
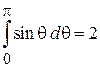 .
.
В результате статистический интеграл вращательного движениямолекулы
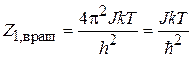 . (П.3.6)
. (П.3.6)






