Тема: Свойства и графики простейших функций

Цель: закрепить теоретические знания и практические умения при решении задач на исследование функции и построения ее графика.

Вид задания: решение вариативных задач

Пояснения к работе:

Для исследования функции надо знать ее основные свойства, а для построения графика функции использовать план:

1).Найти область определения функции (какие значения может принимать переменная «х»)

2).Найти (если это возможно) область значений функции (какие значения может принимать переменная «у»)

3). Определить является ли функция четной или нечетной.

Если выполняется равенство:

А. у (-х)= -у (х), то функция нечетная (график симметричен относительно начала координат т.О (0;0))

В. у (-х)= у (х), то функция четная (график симметричен относительно оси ОУ - оси ординат)

4). Найти основные точки графика: точки пересечения с осями координат.

А. Точки пересечения с осью ОХ: у=0, х=? (это нули функции)

В. Точки пересечения с осью ОУ: х=0, у=?

5).Найти промежутки монотонности функции (при каких значениях «х» функция возрастает или убывает)

Опр .: Функция называется возрастающей на промежутке, если большему значению переменной «х» соответствует большее значение функции.

Опр.: Функция называется убывающей на промежутке, если большему значению переменной «х» соответствует меньшее значение функции.

6) Определить промежутки знакопостоянства функции, т.е. найти, при каких значениях «х», у(х) > 0 и у(х) < 0

7).Найти дополнительные точки(если это необходимо)

Задания:

Выполнить в тетради задания по вариантам:

№ варианта	Задание №1 Найти область определения функции.	Задание №2 Найти нули функции и промежутки знакопостоянства	Задание №3 Определить четность функции	Задание №4 Построить график функции	Задание №5 Найти интервалы возрастания и убывания функции
1в.	y=	y = 3x-	y=2	y =


2в.	y=		y= 2	y= - 2	y=
3в.	y=	y= 3	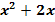y= -	y=
4в.	y=	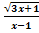	y= 5 tgx	y=	y= 2x+
5в.	y=	y=	y= 3	y=
6в.	y=	y= -2	y= 5	y=