1. Належність прямої площині.
Пряма належить площині, якщо:
1) дві точки цієї прямої розташовані на відповідних горизонталях площини;
2) дві точки прямої розташовані на одній горизонталі площини.
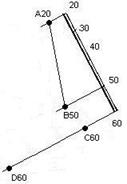Приклад. В площині ∑ побудувати АВ та СD (рис. 11.9).
∑ є АВ;СD.
1. А20В50 є ∑.
2. С60D60 є ∑.
2. Паралельність прямої та площини.
Пряма паралельна до площини, якщо вона паралельна до будь-якої прямої цієї площини.
Рис. 11.9 Рішення задачі складається з двох етапів:
1) на основі умов належності прямої в заданій площині будують пряму;
2) на основі паралельності двох прямих будують пряму, паралельну до площини.
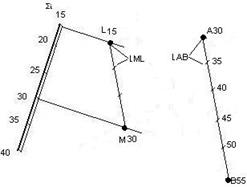
Приклад. Побудувати пряму АВ паралельну ∑ (рис. 11.10).
1. А30 – довільна.
Рис. 11.10 2. АВ║LM.
3. lAB=lML.
4. напрями ЧП однакові;
АВ║LM.
───────
АВ║∑.
3. Перетин прямої та площини.
Для визначення точки перетину прямої і площини необхідно:
1) на масштабі закладання площини визначити дві точки з позначками, які відповідають ЧП двох точок відрізку прямої та побудувати горизонталі через ці точки;
2) через точки, які обмежують відрізок провести дві горизонталі, паралельні між собою таким чином, щоб отримати точки перетину з попередніми горизонталями площини (заключити пряму в допоміжну площину);
3) позначити точки перетину горизонталей та з’єднати їх прямою лінією (лінія перетину допоміжної та заданої площин);
4) продовжити лінію перетину двох площин та задану пряму до взаємного перетину. Отримана точка і є точкою перетину прямої і площини, ЧП якої визначають на основі градуювання заданої
Рис. 11.11 прямої.
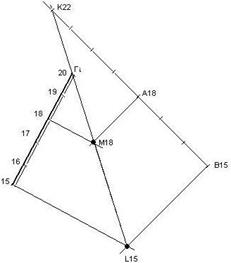
Приклад. Побудувати точку перетину прямої АВ з площиною Г (рис. 11.11).
4. Перпендикулярність прямої і площини.
Пряма перпендикулярна до площини, якщо:
1) закладання прямої паралельне до
Рис. 11.12 масштабу закладання площини;
2) інтервал закладання прямої є величина обернено-пропорційна до інтервалу масштабу закладання площини;
3) напрями зростання ЧП протилежні.
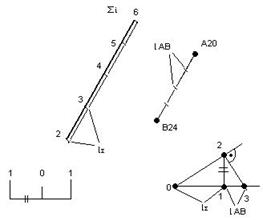
Приклад. Побудувати пряму АВ┴∑ (рис. 11.12).
АВ┴∑;
А20 – довільно.
Для визначення інтервалу закладання АВ будують додатковий графік в наступній послідовності:
1) на горизонтальній шкалі відкладають інтервал масштабу закладання l∑I;
2) з точки 1 піднімаємо перпендикуляр, на якому відкладаємо одиницю лінійного масштабу.
О, 1= l∑I;
1, 2=один. лін. масшт.;
2, 3┴О,2;
1, 3 – lAB.
