Нехай в системі координат 
задана точка 
і ненульовий вектор 
(рис.1).
Очевидно існує єдина пряма 
, що проходить через точку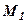 
перпендикулярно напрямкові вектора 
(в цьому випадку називають нормальним вектором прямої ).
Рис.1
Доведемо, що лінійне рівняння
є рівнянням прямої , тобто координати кожної точки 
прямої задовольняють рівняння (1), але координати точки, що не лежить на , рівняння (1) не задовольняють.
Для доведення зауважимо, що скалярний добуток векторів і 
в координатній формі збігається з лівою частиною рівняння (1).
Далі використаємо очевидну властивість прямої : вектори і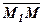 
перпендикулярні, тоді і тільки тоді, коли точка 
лежить на . А за умовою перпендикулярності двох векторів їх скалярний добуток (2) перетворюється в 
для всіх точок , що лежать на , і тільки для них. Отже, (1) – рівняння прямої .
Рівняння (1) називається рівнянням прямої, що проходитьчерез дану точку 
знормальним вектором .
Приклад. Дана точка М(4,1) і вектор 
Необхідно:
1) скласти рівняння прямої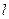 
, що проходить через точку М перпендикулярно вектору 
;
2) перевірити, які з точок М1(0,3), М2(-6,6), М3(3;2,5), М4(8,-1) лежать на прямій ;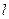
3) побудувати пряму 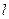і точки М1, М2, М3, М4.
Відповіді: 1) (х-4)+2(у-1)=0; 2)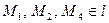 
, 
