Означення. Вектор 
(1) називається лінійною комбінацією 
векторів 
, де 
-деякі числові множники.
У виразі (1) вектор 
отримано в результаті лінійних операцій над векторами 
. Іноді говорять, що вектор лінійно виражається через вектори . Вираз (1) називають також розкладом вектора по системі векторів .
В необхідності розкладу вектора за даними напрямками можна переконатись на такому прикладі.
Дві опори (рис. 9) утримують вантаж під дією сили земного тяжіння 
. Необхідно знайти зусилля на кожну з опор.
Рис. 9
Для розв’язання задачі розкладемо вектор за правилом паралелограма на складові 
і 
, = + , які напрямлені вздовж опор. Величини зусиль 
можна знайти за допомого теореми синусів, розглядаючи паралелограм АВСО, в якому відома діагональ 
і кути 
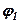і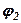 
, які вона утворює зі сторонами ОВ і ОС.
Пропонуємо самостійно переконатись, що
Тепер перейдемо до лінійного вираження вектора за напрямками в більш загальній формі: на прямій, на площині в просторі.
1. Нехай дано два ненульові колініарні вектори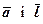 
, 
. Тоді існує число 
таке, що
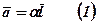
Дійсно, 
можна знайти як відношення 
. Якщо вектори 
однаково напрямлені, 
, то число буде додатним, >0, і якщо 
, то <0.
2. Нехай на площині задані два неколініарні вектори 
, 
½½ 
, і вектор , що належить цій же площині. Знайти розклад вектора за напрямками векторів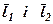 
(рис. 10).
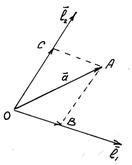
Рис. 10
Побудуємо паралелограм ОВАС, діагональ якого вектор 
, а сторони ОВ і ОС розміщені на напрямках векторів . Тоді
Але 
, тоді за аналогією з (1) існує число таке, що 
. Так само 
.
Отже,
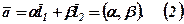
Коефіцієнти розкладу 
називаються координатами вектора в системі векторів .
3. Нехай в просторі задано три некомпланарні вектори 
зведені до спільної точки О і вектор . Тоді має місце розклад:
де 
- деякі числа, називаються координатами вектора в системі векторов 
(рис. 11).
Рис. 11
Для доведення (3) проведемо з точки А (кінець вектора ) пряму 
до перетину з площиною векторів в точці М. Далі, проведемо 
до перетину з напрямком 
в точці 
. ОМАD - паралелограм. Для вектора маємо
.
Вектор 
компланарний з 
, тому згідно (2) існують числа 
такі, що
Крім того, 
, тому за аналогією з (1) існує число 
таке, що 
. Остаточно отримуємо рівність (3).
