Розв’язання. За формулою (1) маємо
=(2-(-1),1-2,4-3)=(3,-1,1).
Приклад 2. Початок вектора 
збігається з точкою 
. Знайти точку 
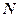, з якою збігається кінець вектора 
.
Розв’язання. Відповідно до формули (1) для вектора 
маємо
(3,1,-5) = 
.
Враховуючи властивість 3о із 2.4 запишемо
,
, 
.
Таким чином знаходимо точку N(1,8,-4).
Приклад 3. Упевнитись, що система векторів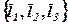 
утворює базис, та знайти координати вектора в цьому базисі, якщо відомі в прямокутній системі координати цих векторів 
, 
, 
, 
.
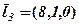Розв’язання. Згідно означення (див. 2.4) вектори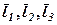 
утворюють базис, якщо вони лінійно незалежні, тобто їх лінійна комбінація 
(де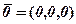 
), тільки тоді, коли 
.
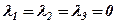Перевіримо це, скориставшись властивостями 1о-3о із 2.4:
Прирівнюючи відповідні координати, отримуємо систему:
Визначник цієї системи
Всі допоміжні визначники 
бо в кожному з них є нульовий стовпець із вільних членів однорідної системи. Отже, згідно формул Крамера 
і, таким чином, вектори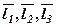 
- лінійно незалежні, а, значить, утворюють новий базис.
Звернемо увагу, що елементи стовпців визначника 
збігаються з відповідними координатами векторів .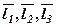
Висновок. Якщо визначник, утворений з координат векторів 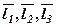, відмінний від нуля, то ці вектори лінійно незалежні, тобто утворюють базис.
Тепер знайдемо координати вектора 
у базисі 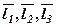, тобто знайдемо числа 
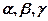такі, що виконується рівність
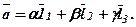
Повторюючи попередні перетворення маємо
Прирівнюючи відповідні координати у лівій і правій частинах рівності, отримаємо систему, яку зручніше розв¢язати алгебраїчним додаванням:
|
.
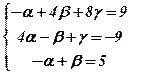
Із 
Таким чином, при 
отримаємо 
.
