Серед декартових систем найбільш поширеною є прямокутна системої координат.
Розглянемо три взаємно перпендикулярні осі ОХ, ОУ, ОZ із спільним початком в точці О - початком координат. Вісь ОХ називається віссю абсцис, ОУ - вісь ординат, ОZ - вісь аплікат (див. рис. 12,а).
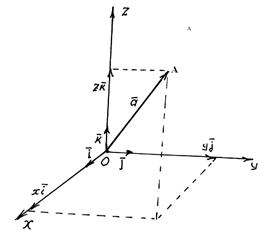
Рис. 12,а
Замість довільних базисних векторів 
зручніше взяти одиничні вектори 
, напрямлені відповідно вздовж осей ОХ, ОУ, ОZ. Такивектори називаються ортами, а утворений ними базис називається ортонормованим,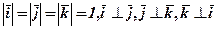 
. Вектор 
, який називається радіусом-вектором точки А(х,у,z) в базисі-векторів 
, має розклад
Очевидно, що довільна точка А(х,у,z) в заданій системі координат одназначно визначається своїм радіусом-вектором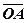 
, а координати точки є координатами її радіуса-вектора.
Звернемо увагу на такий факт. Якщо у попередніх параграфах під виразом “дано вектор” ми розуміли його графічне (геометричне) зображення, то тепер вираз “дано вектор” потрібно сприймати як задання трійки упорядкованих чисел (х, у, z) – координат вектора.
Якщо раніше лінійні дії над векторами здійснювались графічно, то тепер ці операції можна виконувати аналітично, не користуючись рисунком.
Сформулюємо лінійні дії ще раз (див. 1°-3°, § 2.4).
