Виконання вправ. 40 Випишіть всі підмножини множини {а, b, с}

39 Обчисліть а) ; б) ; в) ; г) .

Відповіді: а) 100; б) 1000; в) 161 700; г) 499 500.

40 Випишіть всі підмножини множини {а, b, с}.

Відповідь: , { a }, { b }, {с}, { а, b }, { а, с }, { b, с }, { а, b, с }.

41 Скільки підмножин має множина, яка містить:

а) 6 елементів; б) 10 елементів; в) не містить елементів; г) п елементів. Відповіді: а) 2⁶ = 64; б) 2¹⁰ = 1024; в) 2° = 1; г) 2 ⁿ.

42 Покажіть, що істинна рівність: + + + + 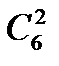+ + 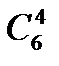= 2⁶.

43 Доведіть справедливість рівностей:

а) + + = + + 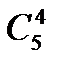; б) + + = + + .

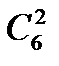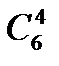44 Обчисліть:

а) + + 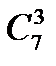+ ; б) + + + .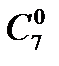

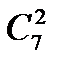Відповіді: а) 64; б) 64.

45 Учень має по одній монеті в 1 коп., 2 коп., 5 коп., 10 коп., 25 коп. Скількома способами він може ці монети розкласти в дві кишені?

Відповідь: 2⁵ =32.

46 У деякому царстві немає двох людей, які б мали однаковий набір зубів. Скільки людей мешкає там, якщо кількість зубів у мешканців утворює всю множину можливих варіантів?

Відповідь: + +…+ + = 2³² = 4 294 967 296.

 

Запишемо всі можливі значення (п = 0, 1, 2,..., т = 0, 1, 2,... п) у вигляді трикутної таблиці.

Враховуючи властивості числа комбінацій , а саме:

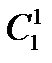1) = = =…= = = 1.

2) = 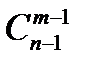+ , тоді цю таблицю легко записати у числово­му вигляді:

Ця таблиця побудована так: у першому рядку записано 1, у другому — з боків від неї по одиниці. У кожному наступному рядку перші та останні числа — одиниці, а кожне інше дорівнює сумі двох найближчих від нього чисел зверху (властивість 2).

Слід зазначити, що числа ряду розміщені на однаковій відстані від його кінців, рівні між собою. Це випливає з рівності:

= . Сума чисел т-го рядка дорівнює 2^m.

Цю трикутну таблицю називають трикутником Паскаля за ім'ям французького математика Б. Паскаля (1623—1662), який займався дослідженням властивостей цієї таблиці й застосуван­ням їх до розв'язування задач та вправ.

 

5 Біном Ньютона

Вам відомі формули:

(а + b)° = 1 (при умові а + b 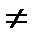0);

(а + b)¹ = а + b;

(а + b)² = α² + 2ab + b². Неважко обчислити, що:

(а+b)³ =(a+b)²·(α+b)=(α²+2αb+b²)(α+b)=α³+2α²b+ ab² + a²b + 2ab² + b³ = а³ + 3a²b + 3ab² + b³;

(а + b)⁴ = (а + b)³ · (а + b) = (а³ + 3a²b + 3ab² + b³)(a + b) = а⁴ + 3а³b + 3а²b²+ ab³ + аb³ + 3a²b² + 3аb³ + b⁴ = а⁴ + 4a³b + 6a²b² + 4ab³ + b⁴.

Відразу кидається в вічі та обставина, що коефіцієнти в пра­вих частинах цих формул дорівнюють числам із відповідних рядків трикутника Паскаля.

Виявляється, що для кожного натурального n правильна і загальна формула:

(а + b)ⁿ = aⁿ + а^n-1b + a^n-2b² +... + 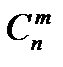a^n-3b^m +... + bⁿ,

яка називається формулою бінома (двочлена) Ньютона, на честь англійського фізика і математика Ісаака Ньютона (1643—1727).

 

Розглянемо основні наслідки із формули Ньютона.

· В розкладі (а + b) ⁿ міститься (n + 1) доданків.

· В формулі Ньютона показники степеня а спадають від η до 0, а показники степеня при b зростають від 0 до п. Сума показ­ників при α і b в будь-якому доданку розкладу дорівнює n — показнику степеня бінома.

· Біноміальні коефіцієнти, рівновіддалені від кінців розкладу, рівні між собою (оскільки = ).

· Загальний член розкладу (позначимо його Т_m+1,) має вигляд

T _m+1 = a^n-mb^m, де m = 0, 1, 2, …, n.

· Сума біноміальних коефіцієнтів дорівнює 2 ⁿ.

Дійсно: + +... + +... + 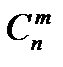= (1 +1) ⁿ = 2 ⁿ.