Рассмотрим упругий стержень, имеющий прямолинейную ось, расположенный в пространстве и закрепленный с помощью опор, которые обеспечивают его недвижимость в любой из двух главных плоскостей инерции поперечного сечения. На рис.13.1,а показана стойка (вертикально расположенный гибкий стержень) относительно пространственной системы координат. Ось x всегда направляется вдоль оси стержня, а две другие оси y и z располагаются в плоскости поперечного сечения и проходят через центр тяжести этого сечения. Они являются главными осями инерции поперечного сечения стержня. При этом условия закрепления стержня в каждой плоскости могут быть одинаковыми или разными. На рис.13.1,б и 13.1,в изображены одинаковые условия закрепления стержня в двух главных плоскостях инерции поперечного сечения стержня.
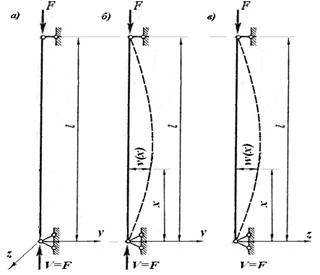
Рис.13.1
Нагрузим стержень вдоль его оси силой F, которая вызывает сжатие этого стержня. В зависимости от длины стержня, размеров и формы его поперечного сечения, а также величины силы F, ось стержня может сохранить начальное прямолинейное состояние (рис.13.1,а) или может перейти в криволинейное деформированное состояние в одной из главных плоскостей инерции сечения (рис.13.1,б и 13.1,в). В таком состоянии стержень может находиться в равновесии, а может потерять его при определенных условиях.
Существует три формы упругого равновесия деформированного состояния стержня: устойчивая, безразличная и неустойчивая.
Упругое равновесие стержня является устойчивым, если этот стержень при каком-нибудь малом отклонении от начального состояния равновесия будет пытаться вернуться к нему после того, как исчезнет причина, вызвавшая отклонение. В этом состоянии стержень будет находиться до тех пор, пока величина силы F будет меньше от величины критической силы Fкр. Устойчивая форма равновесия является безопасной формой деформации стержня.
Упругое равновесие стержня является безразличным, если этот стержень при каком-нибудь малом отклонении от начального состояния равновесия не будет пытаться вернуться к начальному состоянию после того, как исчезнет причина отклонения. В этом состоянии стержень будет находиться при условии, что F = Fкр. То есть безразличное состояние упругого равновесия наступает в случае достижения силой F критического значения Fкр и является предельным состоянием безопасного равновесия.
Упругое равновесие стержня является неустойчивым, если этот стержень при каком-нибудь малом отклонении от начального состояния равновесия будет продолжать отклоняться от начального состояния и после того, как исчезнет причина, вызвавшая отклонение. Неустойчивое равновесие стержня наступает в случае, когда действующая сила сжатия F превышает значение критической силы Fкр, хотя бы на очень малую величину. Такая форма равновесия является опасной и не может быть допущена в элементах зданий и механизмов машин.
При достижении силой F критического значения Fкр наступает безразличное состояние стержня. В этом состоянии деформации стержня очень быстро растут при незначительном увеличении модуля действующей силы и приводят к его разрушению. Поэтому проектная нагрузка не должна превышать допускаемую нагрузку при условии обеспечения устойчивости стержня, то есть, при условии сохранения стержнем устойчивой формы равновесия. Допускаемая нагрузка определяется по формуле:
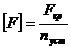(13.1)
где nуст - коэффициент запаса устойчивости, который принимается в пределах его изменения от 1,8 до 3, то есть больше коэффициента запаса прочности в связи с тем, что на устойчивость влияют такие факторы, как начальная кривизна стержня, не центральное действие силы, и тому подобное.
Разделим левую и правую части формулы (13.1) на площадь поперечного сечения стержня (А). Тогда получим:
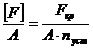, или 
, (13.2)
где 
(13.3)
Таким образом, расчетное сопротивление устойчивости стержня определяется отношением критического напряжения к коэффициенту запаса устойчивости (13.2).
