Статически неопределенными являются системы, внутренние усилия в которых нельзя определить из условий равновесия статики. Для таких систем количество неизвестных усилий превышает количество условий равновесия. Разность между количеством неизвестных усилий и количеством уравнений равновесия статики, которые можно составить для заданной системы, составляет степень ее статической неопределенности. На рис.9.17 приведено пример статически неопределенной системы.
Абсолютно жесткий брус закреплен шарнирно в точке В и поддерживается тремя упругими, вертикально расположенными стержнями. Этот брус нагружен двумя равными по величине внешними силами F, как показано на рис 9.17,а. Все стержни имеют одинаковую длину 3 м. и поперечное сечение круглой формы.
Стержень 3 имеет площадь сечения 2A, а стержни 1 и 2 имеют одинаковую площадь сечения равную А. Стержни изготовлены из стали марки ст.5. Допускаемое напряжение на растяжение равняется
160 МПа. Определить продольные усилия, которые возникают в стержнях, а также диаметры поперечных сечений каждого стержня. Необходимые размеры приведены на рис.9.17,а.
Расчет статически неопределенных систем осуществляется в такой последовательности:
1) Определяем степень статической неопределенности системы как разность между общим количеством неизвестных усилий и количество уравнений равновесия, которые можно составить для заданной системы. От действия внешних сил F в стержнях системы возникают неизвестные усилия N1, N2, N3, а также две составляющие реакции опоры В – вертикальная VВ и горизонтальная HВ. Всего имеем пять неизвестных сил сопротивления, для определения которых можем составить только три уравнения равновесия. Таким образом, заданная система является дважды статически неопределенной;
Рис. 9.17
2) Составляем уравнение равновесия, используя следующие условия равновесия:
ΣXi =0; ΣZi =0; ΣMВ =0.
Первое условие дает возможность определить горизонтальную составляющую реакции опоры В.
HВ =0.
Второе условие приводит к следующему уравнению:
VВ + N1 + N2 + N3 – 2F =0 (9.23)
Используя третье условие, получим уравнение:
N1 ·1 + N2 ·3 + N3·5 – F·3 – F·6=0 (9.24)
3) Чертим геометрическую схему деформации стержней системы и составляем дополнительные уравнения совместимости деформаций этих стержней. От действия внешних сил F абсолютно жесткий брус повернется на некоторый угол вокруг центра шарнирной опоры В. При этом стержни 1,2,3 системы получают удлинение 
, 
, 
соответственно (рис 9.17,б).
Рассмотрим две пары подобных треугольников и составим два геометрических уравнения совместимости деформаций стержней системы:
и 
(9.25)
4) Составляем дополнительные уравнения относительно неизвестных внутренних усилий, которые возникают в стержнях системы.
Для этого продольные деформации стержней в геометрических уравнениях совместимости деформаций (9.25) заменяем продольными усилиями, используя формулу (9.10):
; 
; 
.
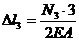Подставим эти значения в зависимости (9.25) и сократим одинаковые величины.
В результате получим следующие уравнения относительно неизвестных усилий
N1, N2, N3:
N2 = 3·N1 (9.26)
N3 = 10·N1 (9.27)
5) Решаем систему полученных уравнений (9.23), (9.26) и (9.27) относительно трех неизвестных усилий:
N1 + 9·N1 + 50·N1 =9·F, откуда N1 = 0,15F,
тогда: N2 = 0,45F и N3 = 1,5F.
Определим, к примеру, усилие в стержнях, если F = 100 кН. Подставим это значение в предыдущие зависимости и получим: N1 = 15 кН, N2 = 45 кН, N3 = 150 кН.
5) Определяем напряжение в поперечных сечениях каждого стержня:
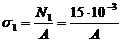МПа; 
МПа;
МПа;
Сравнивая эти напряжения, находим наибольше из них, т.е. 
Приравняем напряжение к расчетному сопротивлению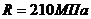 
, находим требуемую площадь поперечного сечения:
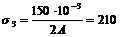, откуда определяем: 
м2, или А =3,57 см2. Найдем необходимый диаметр стержня 3. Площадь круга равняется πd2/4, тогда πd2/4 = 2A = 7,14 см2, откуда имеем:
= 3,4 см.
Стержни 1 и 2 имеют площадь А = 3,57 см2 , тогда диаметр этих стержней будет равняться:
== 
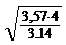= 2,41 см.
Определим напряжение в этих стержнях:
;
.
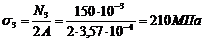
Статически неопределенные системы коренным образом отличаются от статически определенных систем. В статически определенных системах внутренние усилия зависят только от внешних нагрузок. Эти усилия не зависят от размеров поперечных сечений и материала стержней. В стержнях же статически неопределенных систем внутренние усилия зависят от жесткости каждого стержня и возникают не только от действия внешних сил, но и от изменения температуры или технологических условий монтажа конструкции.
